立本溯源优化运算——解析几何运算的几点策略

筅江苏省西亭高级中学　王进

立本溯源优化运算——解析几何运算的几点策略

筅江苏省西亭高级中学王进

解析几何是历届高考试题中的重要组成部分，信息量大，综合性强，运算要求高，且具有一定的技巧性，需要学生“精打细算”，是考查学生数学机智和意志品质的极好的知识载体.但是，根据每年高考统计的结果，解几题的得分都偏低.学生对解几题普遍有“恐惧心理”，主要是恐惧它的繁难冗长的运算过程，而且在于考生往往选择思维方式最简易、计算量最大的方法，这样字母越来越多，式子越来越繁，消不掉，算不出，时常被卡，费时多，很难将运算进行到底，导致半途而废，这就引发了笔者对“优化运算”的思考.本文结合自己的教学体会，谈谈优化解析几何繁难运算的有效策略，供读者参考.

一、通过回归本源、紧扣定义优化运算

定义是事物本质属性的概括与反映.圆锥曲线的许多性质都是由定义派生出来的，对一些圆锥曲线问题，特别是已知条件含有圆锥曲线上的点到焦点（或准线）的距离、离心率等，若能灵活地运用定义去求解，把定量的计算和定性的分析有机地结合起来，则往往能获得题目所固有的本质属性，达到准确判断、合理运算、灵活解题的目的.

圆锥曲线的定义刻画了圆锥曲线上动点的本质属性，有着丰富的内涵，利用定义把问题的定性分析和定量计算有机结合起来，思路清晰，易于找到问题的突破口.

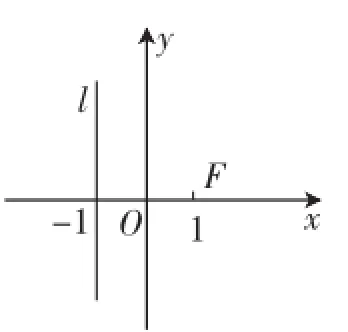
图1　

例1如图1，已知点F（1，0），直线l：x=-1，P为平面上的动点，过点P作直线l的垂线，垂足为Q，且QBBP·QBBF

（1）求动点P的轨迹C的方程；

（2）过点F的直线交轨迹C于A、B两点，交直线l于点M，已知求λ1+λ2的值.

解析：（1）设点P的坐标为（x，y），则点Q的坐标为（-1， y），由，得（x+1，0）（2，-y）=（x-1，y）（-2， y），化简得y2=4x.

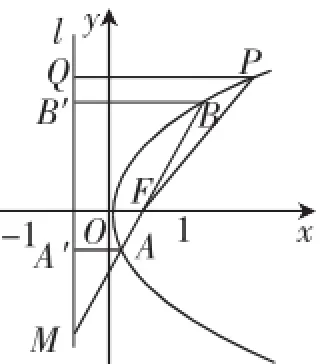
图2　

过A、B分别作准线l的垂线，垂足分别为A′、B′，则由比例性质和抛物线定义得

评注：圆锥曲线的原始定义应用广泛，对于圆锥曲线中与焦点有关的最值问题、轨迹问题、计算或证明问题，用定义来解会更简捷.

二、利用平几知识优化运算

解决解析几何问题时，往往需要求解涉及含多个参数的两个以上方程组成的方程组，运算较为复杂，运算能力稍差的同学难以准确迅速求解，甚至半途而废；若能联想到题目所涉及图形的几何性质，并利用有关几何性质来解决问题，常常可以峰回路转，达到巧妙解题的效果.

例2已知点P到两定点M（-1，0）、N（1，0）的距离比为，点N到直线PM的距离为1，求直线PN的方程.

解析：本题若按常规做法为：设P（a，b），则直线PM的方程为y，即bx-（a+1）y+b=0，于是1=|NH|=

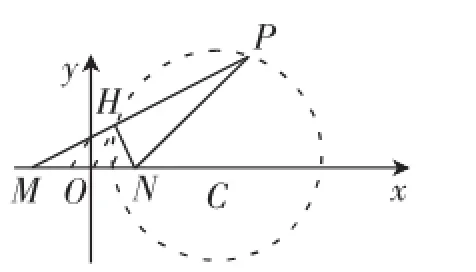
图3　

于是kPN=tan∠PNM=±1.

因此直线PN的方程为y=±（x-1）.

评注：本题重点考查运算能力，这对考生提出了较高的要求.通过对比上述通法与巧法，读者很容易看出：运用平面图形的有关几何性质来解决一些解析几何问题，可以有效地避免复杂的代数运算，达到简捷解题的目的.2013年高考山东卷理科第22题第（Ⅱ）问也可以用此策略来求解.

三、通过设而不求来优化运算

所谓“设而不求”，就是在解题时设一些辅助元（参数）作为媒介，在解题过程中并不求出这些辅助元，只用它们连接已知量和未知量，最后又巧妙地将其消去，求出未知量.在研究直线与二次曲线时，经常讨论中点、直线方程、弦长等问题，其惯用方法就是“设而不求”.它不仅可以有效解决相关问题，还可以减少计算量.

（1）求椭圆C的标准方程.

（2）设F为椭圆C的左焦点，T为直线x=-3上任意一点，过点F作TF的垂线交椭圆C于点P、Q.证明：OT平分线段PQ（其中O为坐标原点）.

（2）证法1：由（1）可得F的坐标是（-2，0），设T点的坐标为（-2，m），则直线TF的斜率kTF=-m.

当m=0时，直线PQ的方程是x=-2，也符合x=my-2的形式.

设P（x1，y1），Q（x2，y2），将直线PQ的方程与椭圆C的方程联立，得

，消去x，得（m2+3）y2-4my-2= 0，其判别式Δ=16m2+8（m2+3）>0，所以y1+y2=

又直线OT的斜率kOT=所以点M在直线OT上，因此OT平分线段PQ.

证法2：由（1）可得F的坐标是（-2，0），设T点的坐标为（-3，m），则直线TF的斜率kTF=-m.

当m≠0时，直线PQ的斜率kPQ=

设P（x1，y1），Q（x2，y2），M（x0，y0），则①，=1②.

又直线OT的斜率kOT=-，所以点M在直线OT上.

当m=0时也适合，因此OT平分线段PQ.

评注：证法2利用“点差法”，采用整体代换，避免了证法1中直线代入圆锥曲线，再利用韦达定理的繁杂计算.“点差法”是解决“中点弦”问题的常用方法，它巧妙地运用了“设而不求”的思想，有效地减少了计算量.

四、巧用参数方程或极坐标优化运算

参数方程把曲线上的点的横、纵坐标分别通过参数直接表达出来，比较清楚地指明了曲线上的点的坐标特征，对于圆锥曲线上与动点有关的最值，以及处理两线段长度的积和差等问题，有着普通方程无可比拟的优越性.例4如图4所示，椭圆C：=1的顶点为A1，A2，B1，B2，焦点为F1，F2，|A1A2|=，S荀A1B1A2B2=2S荀B1F1B2F2.

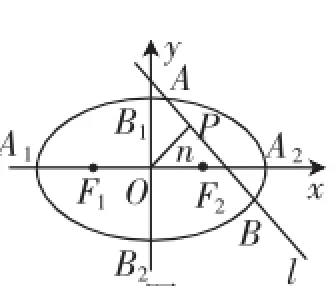
图4　

（1）求椭圆C的方程；

（2）设n是过原点的直线，l是与n垂直相交于点P，与椭圆相交于点A、B的直线，|OPPP|=1，是否存在上述直线l使APPP·PP

PB=1成立？若存在，求出直线l的方程；若不存在，请说明理由.

（2）设直线l的倾斜角为θ，P（x0，y0），则有：

故不存在这样的直线l.

评注：本题若采用直线斜截式方程来求解，不仅要分类讨论，还要应用点到直线的距离，向量数量积等列方程组，通过判别式、韦达定理来探讨方程组解的情况，容易陷入繁冗的运算而不能自拔，导致解题失败.引入直线参数方程，巧妙地将点到直线的距离转化到P点的坐标中，向量的数量积能用参数的乘积来表达，从而突破难点，简化了运算.

圆锥曲线极坐标方程形式的统一给人以美感，结论的简洁是任何一种形式都无法媲美的，当问题涉及圆锥曲线的焦点弦时，利用极坐标方程往往能收到意想不到的效果.

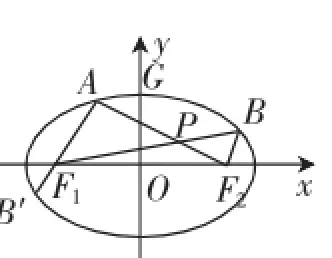
图5　

（Ⅰ）求椭圆方程；

（Ⅱ）设A、B是椭圆上位于x轴上方两点，且直线AF1与直线BF2平行，AF2与BF1交于点P.

（1）若AF1-BF2=，求直线AF1的斜率；

（2）求证：PF1+PF2是定值.

（Ⅱ）（1）以F1为极点，F1F2所在直线为极轴，延长AF1交椭圆于点B′.

设∠AF1F2=θ，AF1=p1，B′F1=p2，则有AF1=p1

由椭圆对称性有BF2=B′F1=

由AF1-BF2=，得

（2）由p1=

评注：本题若按常规思路用直角坐标系方程求解，需要联立解方程组，运用两点间距离公式来求解，计算量较大；而用极坐标方程，几何条件特征明显，利于建立相关的关系式和表达式，再进行相应的运算，能简化计算和论证，使问题的解决思路变得统一、顺畅，大大优化了解题的过程.

五、利用向量优化运算

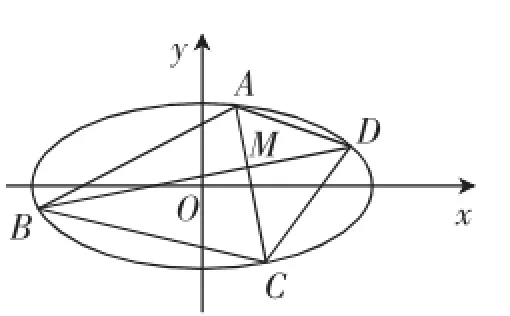
图6　

（1）证明：AC⊥BD；

（2）略.

常规思路：要证AC⊥BD，即证A为此可设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），而后利用平面内两点间距离平方公式对条件等式进行化简变形.

尝试：设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则|AB|2=（x1-x2）2+（y1-y2）2，|CD|2=（x3-x4）2+（y3-y4）2，|BC|2=（x3-x2）2+（y3-y2）2，|AD|2=（x4-x1）2+（y4-y1）2.又|AB|2+|CD|2= |BC|2+|AD|2，从而（x1-x2）2+（y1-y2）2+（x3-x4）2+（y3-y4）2=（x3-x2）2+（y3-y2）2+（x4-x1）2+（y4-y1）2，然而对于上式其变量之多、结构之复杂，绝大部分同学看到都会心生畏惧，力不从心.

调整思路：考虑到线段长的平方等于该线段所对向量的平方，于是通过向量搭桥，可将转化为进一步转化即，然后展开化简求证

评注：通过向量搭桥来实现条件的合理转化是本题的一大亮点，它有效地避开了距离平方所带来的复杂运算，促使了整个解题过程简捷而富有实效，很值得我们探究和回味.

简化解析几何计算的方法和技巧还有许多，本文只给出其基本的五种方法.希望通过本文的阐述，能给读者带来一些启发，进而避开烦琐的解几运算，优化解题过程，最终使自己变得更加睿智.Z