四大原则在手 函数解题无忧
江苏 朱建新
(作者单位:江苏省前黄高级中学国际分校)
四大原则在手 函数解题无忧

函数是高中数学的重要内容,它引入了变量,让学生在动态中探寻数学的秘密.然而,学生在学习、复习过程中往往会产生比较大的困难,比如思维上有漏洞,解题时胡乱套用方法、模式等,本文结合笔者多年来的教学感悟,总结了复习好函数的一些原则,按照这些原则,函数的解题会变得清晰有趣,可以轻松以不变应万变.
一、定义域优先原则
【例1】已知函数f(x)=log3x+2,x∈[1,9],求函数g(x)=f2(x)+f(x2)的值域.
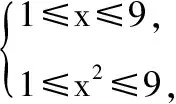
【评注】本题如果不考虑g(x)的定义域,则缺少函数的三要素之一,从而导致值域错误.
【例2】已知奇函数f(x)是定义在(-3,3)上的减函数,求不等式f(x-3)+f(x2-3)<0的解集.
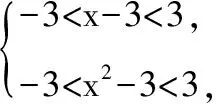
【评注】这个不等式问题本质还是函数问题,确定一个函数必须优先求出定义域,这样才能保证求解的范围不被放大.
二、单调性为核心原则
【解析】易知f(x)在[0,+∞)上单调递增,在(-∞,0)上也单调递增,且x=0时,4x-x2=f(0),所以可得f(x)在(-∞,+∞)上单调递增,故f(2-a2)>f(a)可得2-a2>a,解得-2 【评注】本题由于成功研究了f(x)的单调性,从而抓住了f(x)的本质,避免了因为分段带来的复杂讨论. 【评注】本题f(x)导数的条件使我们研究出了g(x)的单调性,从而不等式转化为g(x)的不等式,利用g(x)的单调性求解. 又a<0,所以-3≤a<0. 【评注】本题由条件中的不等式获得了新函数g(x)的单调性,然后用导数解决问题,如果不思考单调性,则题目条件无从下手. 【例6】已知函数f(x)=x|x-a|+2x,若a>0,关于x的方程f(x)=9有三个不相等的实数解,求实数a的取值范围. 【评注】本题变形产生了三个简单的函数的图象,通过观察图象与图象的交点个数,列出简单的式子,求出了实数a的取值范围,避免了复杂的分类讨论. 【解析】易知f(x)在[0,+∞)上单调递增,在(-∞,0)上单调递增,可画出f(x)的图象, 由图象知,f(x) 的图象位于函数y=5的图象下方的部分对应的自变量的范围为(-∞,1), 所以不等式f(2x2-|x|)≤5可转化为2x2-|x|≤1,解得0≤|x|≤1,即[-1,1]. 【评注】本题从函数图象角度思考不等式f(x)≤5,从而不等式f(2x2-|x|)≤5可转化为2x2-|x|≤1,避免了纯代数思考的复杂运算. 【评注】本题如果忽略了f(x)的对称性思考,则不等式无法转化,从而无法突破运算的障碍. 又因为f(-x)=(-x)3+sin(-x)=-x3-sinx=-f(x),所以可知f(x)为奇函数. 由x3+sinx-2a=0,4y3+sinycosy+a=0,可得f(x)=x3+sinx=2a,f(2y)=(2y)3+sin2y=-2a,所以f(x)+f(2y)=0. 【评注】本题只考虑单调性运算有障碍,不能成功解决问题,借助奇函数性质的帮忙才能运用单调性解决问题. 【例10】已知函数f(x)是定义在(-∞,+∞)上的奇函数,若对于任意的实数x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),求f(-2 011)+f(2 012)的值. 【解析】当x≥0时,由f(x+2)=f(x)知f(x)周期为2,所以f(2 012)=f(0)=0, 又f(x)为奇函数,所以f(-2 011)=-f(2 011),再由周期性得f(2 011)=f(1)=1, 所以f(-2 011)+f(2 012)=-1+0=0. 【评注】本题考查了函数的对称性和周期性,两个性质熟练运用,轻松获得答案. (作者单位:江苏省前黄高级中学国际分校)

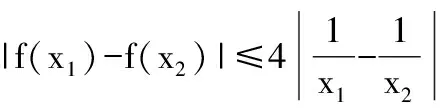
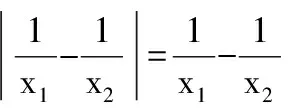
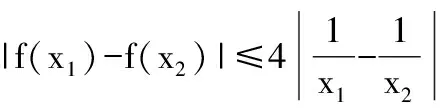
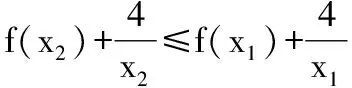
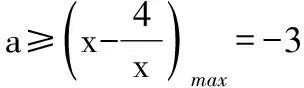
三、图象为归宿原则
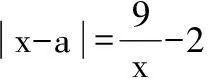
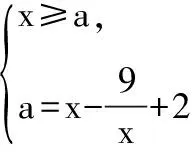

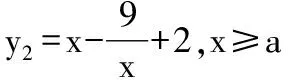
四、对称性与周期性辅助原则