对一光线反射问题的再思考

朱胜强

(南京外国语学校 210008)

本刊2016年第9期《应用空间向量与三角函数解题的一个范例》(以下简称文[1])一文中介绍了物理教师给同学们提出的一个传统光学问题:

一束太阳光与水平面成40°角的方向射来,要使反射光线沿水平方向射出,平面镜与水平面成多少度角摆放?

这是一个很有趣味的问题.直观感觉有两种结果,也就是镜面与水平面成70°角或20°角.却不知不觉犯了与文[1]所指的同样错误.原来学习光学让我们产生了思维定势,误将问题限定在同一平面中考虑.其实,许多人都有这样的生活体验,当阳光射入室内时,用一面镜子可将光线反射向每一个角落.因此,这一问题应在三维空间中进行思考.这就需要借助处理空间线面关系的数学模型.所以,该问题是体现数学与生活及其它学科间联系,培养学生解决问题能力的好素材,有助于学生认识数学的应用价值.

文[1]给出了用空间向量与三角函数的解决问题的方法,得到了一般性的结论,拜读后很受启发.然而,从应用于教学的角度来看,感到有进一步完善的必要.也就是解决问题的过程对学生来说稍显复杂,数学基础一般的学生,很可能会满怀好奇地开始,未多久便被烦琐的运算弄得晕头转向,最后可能无功而返,这可能不利于培养学生数学学习的积极情感.由此引发了笔者的思考,为使该问题的教学价值得以充分发挥,是否有较为简洁、在教师引导下学生容易发现或容易接受的解决问题的方法呢?

1 对空间向量法的改进

以入射点O为坐标原点,水平面为xOy平面,过入射光线且与水平面垂直的平面为yOz平面,建立空间直角坐标系.设入射光线与以O为球心,1为半径的球面的交点为A,反射光线与该球面的交点为B,z轴的正半轴与球面的交点为Z.

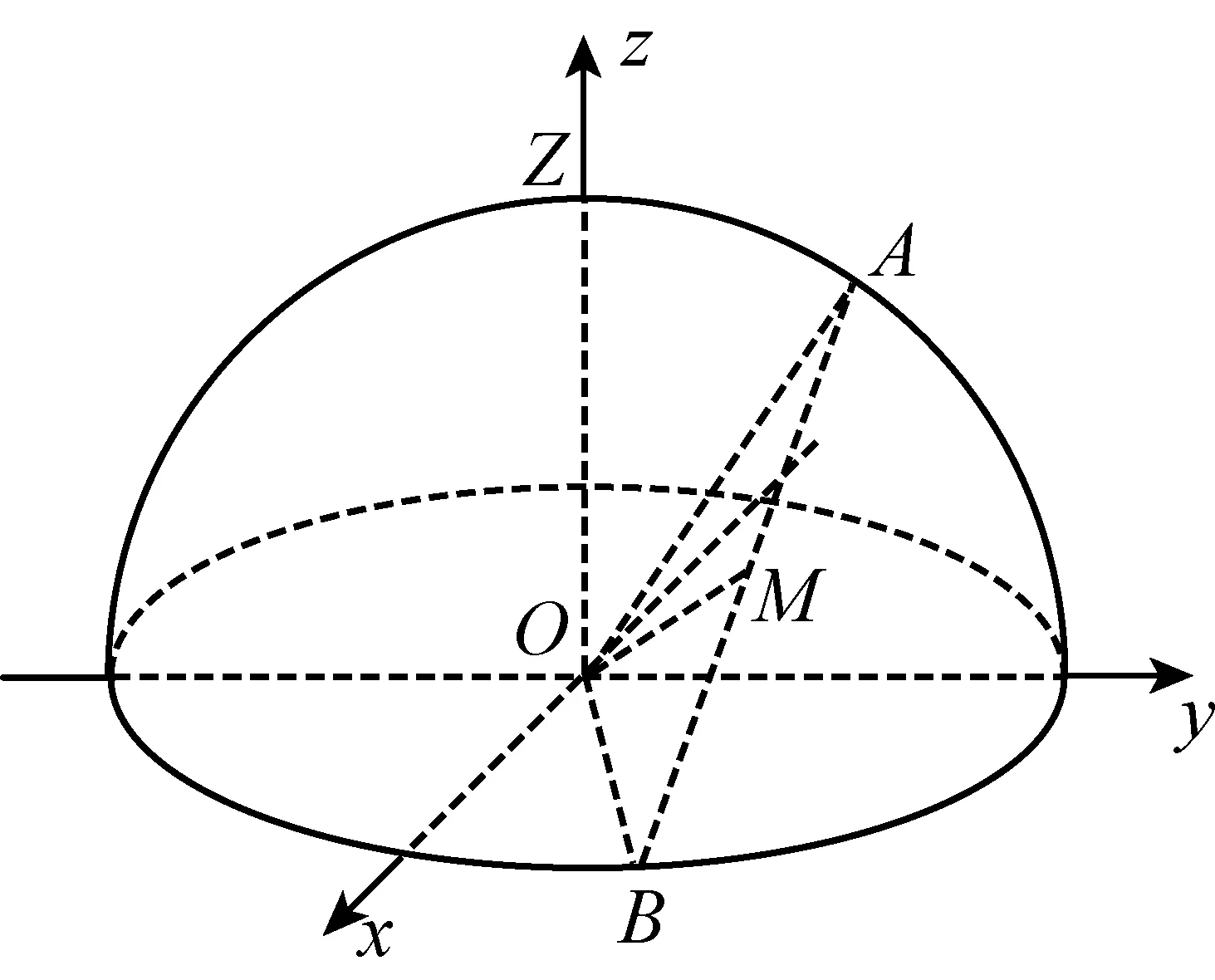
图1

设入射光线与水平面所成的角为α(0°<α<90°),则点A的坐标为(0,cosα,sinα).因为反射光线在水平面内,所以设反射光线与x轴的正半轴所成的角为β(即从上向下看,将x轴正半轴按逆时针方向旋转到与OB重合时转过的最小正角,0°≤β<360°),则B点坐标为(cosβ,sinβ,0).

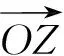
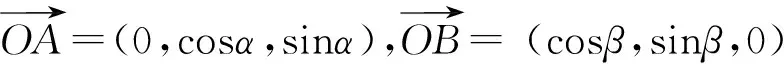
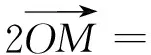
= (cosβ,cosα+ sinβ,sinα).

可以看出,镜面与水平面所成的角不仅与α有关,还与β有关.

如果β= 90°,则反射光线与y轴的正半轴重合.此时

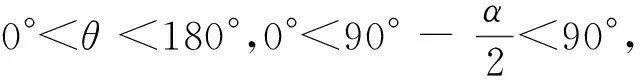
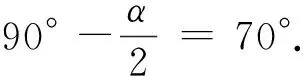
如果β= 270°,则反射光线与y轴的负半轴重合.此时

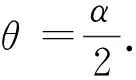
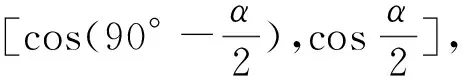
与文[1]相比,这里没有去求镜面法线的单位向量,而是直接由入射光线与反射光线方向上的单位向量的和得到镜面法向量,从而简化了运算.

2 直观展示镜面的变化规律

用空间向量虽然解决了问题,但依赖的是抽象的代数运算.当反射光线在水平面上改变方向时,镜面相对于水平面位置发生着怎样的变化,还是说不清楚.是否能较直观地展现出来呢?

由上可知,镜面过点O且与OM垂直.所以,只要弄清射线OM的方向是如何变化的,镜面的变化规律也就清楚了.为此,考虑入射角α不变,B在xOy平面内的单位圆上变化时,点M的变化情况.

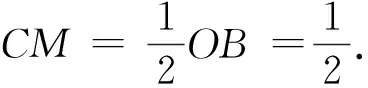
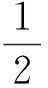
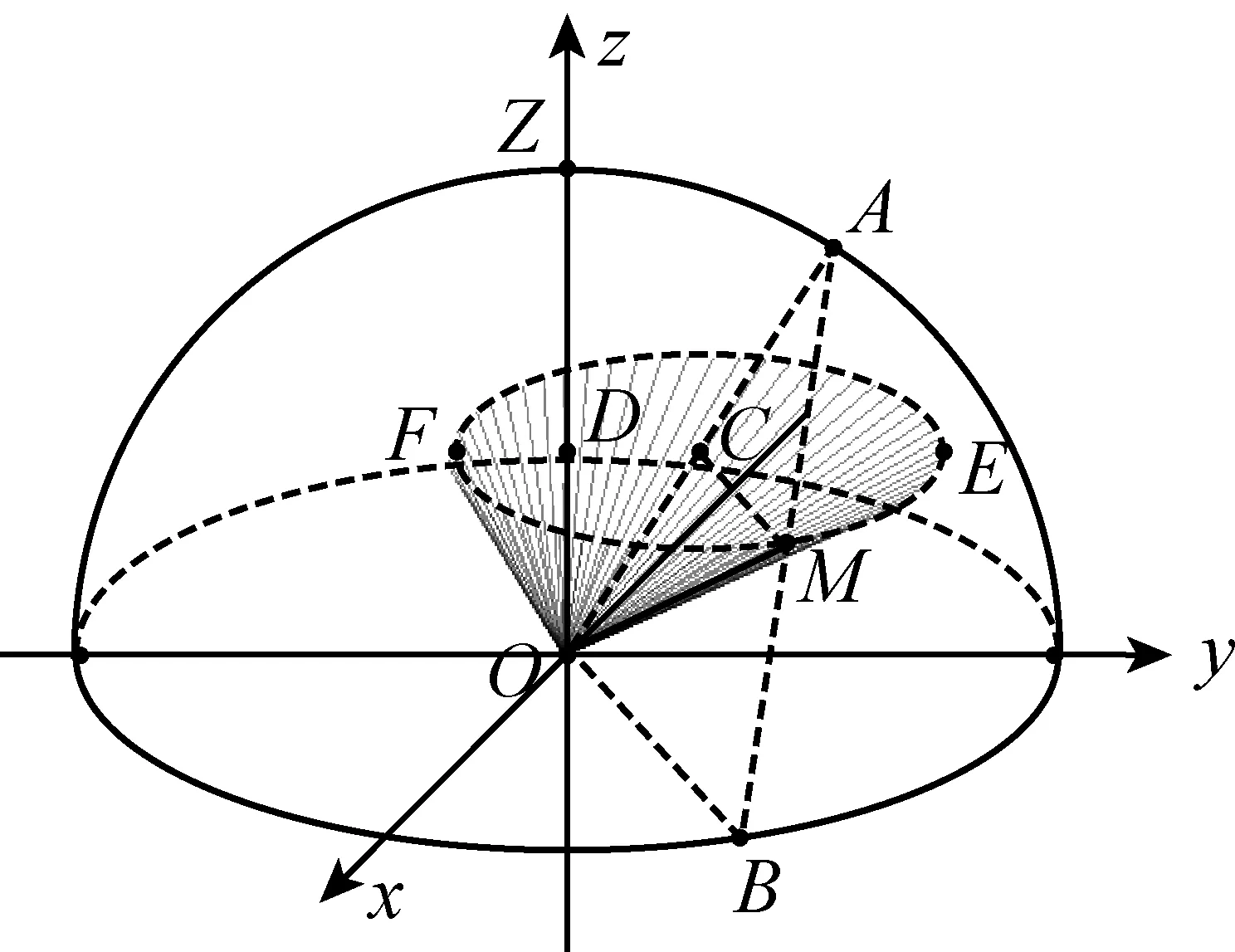
图2

有了镜面变化规律的直观展示,我们又可在此基础上再度考察镜面与水平面所成的角.

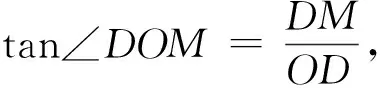
图3

设直线DC与圆C的交点为E,F.则当M位于E或F时,DM分别取得最大值与最小值.此时,∠DOM也相应地取得最大值与最小值.注意到OEOF(∠AOy的内角平分线与外角平分线垂直),∠COD= 90° -α,所以当M位于点E时,B位于y轴的正半轴;当点M位于点F时,点B位于y轴的负半轴.

如果反射光线OB与x轴的正半轴所成的角为β(0°≤β<360°),如何确定镜面与水平面所成的角呢?(图4)

图4

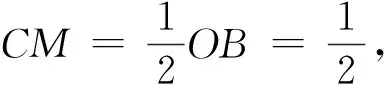
∠DCM= 90° +β(或|270° -β|).

所以,DM2=DC2+CM2-

2DC·CMcos∠DCM

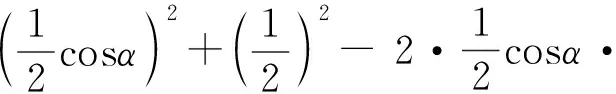
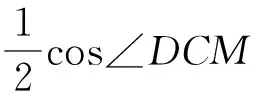
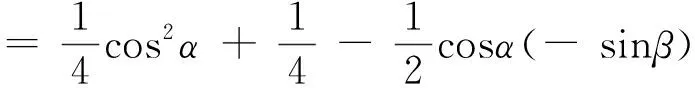
又因为ODDM,所以,

OM2=OD2+DM2

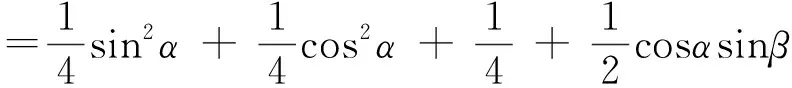
因此,一旦摸清了镜面的变化特点,即使没有掌握选修内容中的空间向量知识,也可以较为简洁地解决这一问题.

3 从学生熟悉的模型出发思考

用单位球面衬托镜面的变化,从某种层度上讲是受向量方法的影响,也就是将向量的模特殊化,这类似于三角函数中借助单位圆思考问题.对于不熟悉空间向量的学生来说,也许会有一定的难度.在立体几何初步教学中,长方体或直棱柱等几何体是学生较为熟悉的空间模型,在这样的几何体中研究问题,学生往往更能找到“空间感觉”.因此,我们也可以尝试用学生熟悉的模型来研究问题.

在入射光线上取一点A,使AO= 1,设A在水平面上的射影为H.在反射光线上取一点B,使BO= 1.以△OBH为底面,AH为侧棱,作直三棱柱OBH-IJA(如图5).

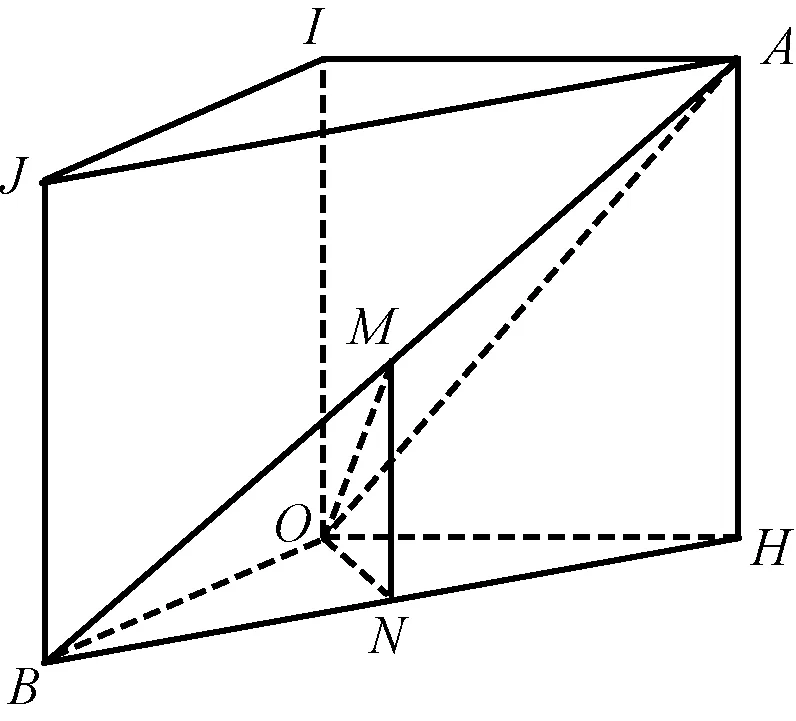
图5

因为OA=OB= 1,所以△OAB为等腰三角形.取AB中点M,连结OM,则OM为∠AOB的平分线,因此OM是镜面的垂线.又OI是水平面的垂线,所以,OI与OM所成的角∠IOM即为镜面与水平面所成的角.取BH中点N,连结MN,可知∠OMN= ∠IOM.

设∠BOH=θ(0°<θ<180°).

由∠AOH=α(0°<α<90°),知AH=sinα,

又在△OBH中,OB= 1,OH= cosα,∠BOH=θ,

所以BH2= 1 + cos2α-2cosαcosθ.

所以AB2=AH2+BH2

= sin2α+ 1 + cos2α-2cosαcosθ

= 2-2cosαcosθ.

所以OM2=OB2-BM2

注意到此处的θ与前面的β间满足关系cosθ= sinβ,因此所得结果与前面是一致的.

当代著名数学家P.R.哈尔莫斯曾指出:问题是数学的心脏.由此可见问题在数学教学中的重要性.美国著名的数学问题解决专家匈菲尔德还给出了“好问题”的五条审美原则,即一个好问题必须满足:⑴是容易接受的(不需要大量技巧);⑵有多重解题方法(或者至少有多重思路);⑶蕴含了重要的数学思想(好的数学);⑷不故意设陷阱;⑸可以进一步开展和一般化(导致丰富的数学探究活动).因此,问题的“好”与“不好”不是只片面地取决于问题本身,还要看问题提供给谁思考,看教师对问题的认识程度.通过对文[1]中问题的再度研究可以体会到,教学中的“好问题”不尽是天然的,有时是在教师从学生的视角对它进行深入思考、发掘后,才充分显现出它的教学价值.