高考中二项式定理常见题型解析

■甘肃省白银市第一中学 胡贵平

■甘肃省白银市第一中学 胡贵平

二项式定理在高考中是最常考的知识,它常以小而灵活的选择题、填空题的形式出现,虽然难度不大,但常考常新,解法灵活,下面通过高考题对二项式定理常见题型进行归纳。

一、求二项展开式的某一项系数

1.“(a+b)n”型的展开式

点评:(a+b)n展开式的二项式系数与各项的系数是两个不同的概念,前者是指,与a,b无关;后者是指该项除字母以外的部分,各项的系数不仅与各项的二项式系数有关,而且也与a,b有关。

2.“(a+b+c)n”型的展开式

例2 (2015年新课标Ⅰ卷)(x2+x+y)5的展开式中,x5y2的系数为( )。

A.10 B.20 C.30 D.60

解法一:(x2+x+y)5的5个因式中,2个因式中取x2,剩余的3个因式中1个取x,其余的因式取y,因此x5y2的系数为C25C13C22=30,故选C。

解法二:(x2+x+y)5=[(x2+x)+y]5,二项展开式通项为yk,令k=2,(x2+x)3的二项展开式通项为Tr+1=,再令6-r=5,得r=1,因此x5y2的系数为=30,故选C。

点评:(a+b+c)n的展开式中apbqcr的,其中p+q+r=n。因为(a+b+c)n的展开式中的项apbqcr是在n个因式中,p个因式中取a,q个因式中取b,r个因式中取c乘积而得,而p个a,q个b,r个c作成的n个不完全相异元素的全排列数

3.“(a+b)n(c+d)m”型的展开式

例3 (2013年四川卷)(1+2x)3(1-x)4的展开式中x2的系数为____。

解:(1+2x)3的展开式的通项为Tk+1=·(2x)k,k=0,1,2,3。

(1-x)4的通项为(-x)r,r=0,1,2,3,4,所以(1+2x)3(1-x)4展开式中的一般项为Ck3·Cr4·2k·(-1)r·xk+r。令k+r=2,得所以展开式中x2的系数为

点评:(a+b)n(c+d)m的展开式中的一般项为,k=0,1,2,…,n;r=0,1,2,…,m。

4.“(a+b)m+(a+b)m+1+(a+b)m+2+…+(a+b)n”型的展开式

例4 (x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5展开式中,x2的系数为____。

解法一:由题意知-(x-1)2,(x-1)3,-(x-1)4,(x-1)5展开式中x2的系数为-C02,-C13,-C24,-C35,所以原式中x2的系数为-C02-C13-C24-C35=-20。

解法二:由等比数列求和公式,可得:

点评:(a+b)m+(a+b)m+1+(a+b)m+2+…+(a+b)n可以看作首项是(a+b)m,公比是(a+b)的等比数列的前n-m+1项和,通过等比数列求和公式减少项数,简化运算。

二、求二项展开式的系数和及相关题

1.二项展开式的系数和

例5 (2015年新课标Ⅱ卷)(a+x)·(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=。

解:设(a+x)(1+x)4=a0+a1x+a2x2+…+a5x5,展开式中x的奇数次幂项系数分别为a1,a3,a5,于是a1+a3+a5=32。当x=1时,16(a+1)=a0+a1+a2+a3+a4+a5;当x=-1时,0=a0-a1+a2-a3+a4-a5。两式相减得16(a+1)=2(a1+a3+a5),所以16(a+1)=2×32,解得a=3。

点评:求二项展开式的系数和差这类题的常用解法是赋值代入,多项式f(x)的各项系数和为f(1),奇数项系数和为

2.二项式系数的最值

例6 (2013年高考新课标Ⅰ卷)设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=( )。

A.5 B.6 C.7 D.8

解:由题意知,由13a=,解得m=6,故选B。

点评:二项式定理中应注意区别二项式系数与展开式系数,各二项式系数和为,奇数项的二项式系数和与偶数项的二项式系数和相等,即

点评:(a+b)n的二项展开式中,与首末两项“等距离”的两项的二项式系数相等;如果二项式的幂指数是偶数,中间一项的二项式系数最大;如果二项式的幂指数是奇数,中间两项的二项式系数相等且最大。

3.二项式系数和

例7 (2015年湖北卷)已知(1+x)n的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式系数和为( )。

A.212B.211C.210D.29

解:因为(1+x)n的展开式中第4项与第8项的二项式系数相等,所以,解得n=10。所以二项式(1+x)10中奇数项的

三、与二项展开式交汇型

例8 (2012年湖北卷)设a∈Z,且0≤a≤13,若512012+a能被13整除,则a=( )。

A.0 B.1 C.11 D.12

解:512012+a=(52-1)2012+a

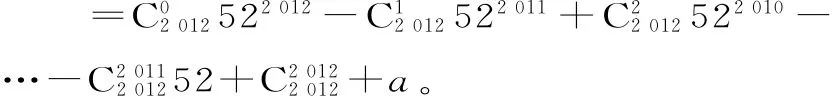
由于52含有因数52,故能被52整除。

要使得512012+a能被13整除,且a∈Z,0≤a≤13,则a+1=13,所以a=12,故选D。

点评:二项式定理的主要应用就是近似计算和证明整除性问题或求余数,应用首尾几项进行放缩证明不等式。利用二项式定理处理整除问题时,要巧妙地将非标准的二项式问题化归到二项式定理的情境上来,变形要有一定的目的,要凑出相关的因数。