在函数教学中渗透数形结合思想实践例谈

□ 海南省澄迈县澄迈中学 王上兴

数学思想是学习数学知识的灵魂，是知识转化为能力的途径，也是解决数学数学问题的根本。在数学教学中，注重知识的传授不是一个完整的教学，而是要重视数学思想的培养。只注重知识的传授不利于学生对知识的灵活运用，使学生知识停留在初级阶段。数形结合思想通过“以形转数”、“以数构形”的方式，使得一些抽象的数字问题得到直观化、形象化的转变，这有助于提高学生思维和数学素养，可以让学生把握数形结合思想。数学课堂教学有两条线：一条是明线，即数学知识；一条是暗线，即数学思想方法。优秀的例子、习题所体现的数学知识无疑是重要的，但其蕴涵的数学思想对学生能力培养更显重要。可是如何去挖掘优秀例题和习题呢？本文结合自己的教学实践，阐述了一些自己的观点，对于挖掘优秀例题和习题有很大的帮助。

一、挖掘教材，逐步培养数形结合意识

“数”与“形”是数学问题的概括和抽象，从某个角度来看，“数”与“形”是相互独立的。但是在某种条件之下，它们是可以相互转化。要让学生形成运用数形结合的意识，首先要在教学过程中让学生不断地经历数形结合的学习过程，就是说见得多了才能加深印象。教学过程中如果将蕴含于教材中的内容重新整理，挖掘教学内容的潜在价值，经过恰当的点拨和灌输，可以促使学生数形结合的意识逐步形成，为今后运用数形结合解决问题做好准备.

新课标指出“初中数学是研究数量关系和空间几何图形的一门学科”。在学习函数之前，学生已接触过用几何图形表示数量关系，也曾从观察图形得出数量关系，但这些对于培养学生数形结合思想，是远远不够的，而函数便是展示数形结合的一种很好的体现。若在求解函数的问题中，学生的“数形结合”意识十分清晰，他们就能通过以“形”转“数”、以“数”构“形”的方式解决函数中的问题；若学生的数形结合的意识十分模糊，他们就没意识到运用数形结合可以解决问题，也不会判定哪些问题中可以运用数形结合？自然也不懂得怎样把“代数”化为“几何”来求解或把“几何”看作“代数”来求解，这些都需要教师在教学中进行恰当的引导，并用语言表述题目所隐含的数形结合的思想，使学生数形结合的意识逐步清晰。而初中教材有关函数的内容总是将同一个函数的数量关系 (解析式）和几何图形（图象）放在一起进行研究，将某个问题从数与形的层面呈现出来，有助于培养学生的数形结合意识。在此基础上，教师如能善于运用教材，充分挖掘、适当引导，更加有效促进学生数形结合意识的形成。例如：我在《二次函数y=ax2图象》教学时，利用以下这道题进行教学。

例1、已知一个正方形的边长是xcm，面积为ycm2

（1）写出y与x的函数关系式；

（2）当y=25时，边长x是多少？

（3）画出此函数的图象。

分析：（1）根据正方形面积求解方法，即可求出y与x的函数关系式；

（2）当y=25时，即y=25入函数解析式中，可求出正方形的边长x的值

（3）因为是二次函数的实际问题，所以画二次函数的图象在第一象限即可；

解：（1）∵ 正方形边长为x，其面积为y，

∴y=x2，

∴y与x的函数关系式为y=x2；

（2）∵ 正方形面积为25

∴x2=25，

解得：x=5或 x=-5（舍去），

∴正方形的边长是5cm；

（3）如图所示：

在函数图象概念学习时，先让学生分析一个边长为x的正方形与其面积S之间的数量关系（解析式）S=x2（x＞0），再通过列表、描点、连线画出图形，然后利用坐标平面的关系，最后绘制函数图像的概念。在重点学习函数图象画法的同时，我们可以简要地给学生强调：（1）“数量”是可以用“图形”来表示的；（2）函数（数量关系）都只能用一个函数图象（图形）表示这两个事实，加深学生数与形之间可以紧密相连的印象。

在中学阶段，教材中的几种函数基本上都是按照这种顺序来安排的，即从函数的概念到函数的图像，由函数的图像到函数的性质，再到函数图象和性质的应用。那这几种函数分别是：正比例函数、一次函数、反比例函数和二次函数，这四种函数都可以以“数形结合”的形式存在。教师在教学过程中，只要把握时机适当点拔，在教学过程中蕴含于教材的内容重新整理，挖掘潜在的价值。让他们今后运用数形结合思想去解决问题打好基础。

二、结合应用，认识数形对应关系

在函数教学内容中，每一个函数都可以画出它的图像，图像是函数解析式的一种直观表示，函数解析式都是图像上点坐标之间的数量关系；在函数解析式中，函数中的自变量为坐标中的横坐标，自变量对应的函数值为纵坐标，两者组成的点却在函数的图象上，反之函数图象上的每一点的坐标分别是函数自变量x的某一个值及其相应的函数值y。因此，函数的“数”（函数解析式）和“形”（图象）是一种对应关系，是某变化过程中两个量间自变量和函数间依赖关系的两种不同的表示形式。有了函数的图象就能写出函数的表达式，有了函数关系式同样可以画出函数的图象，说明了数与形之间有着对应关系。例如，一次函数图象是一条直线，坐标平面上的直线也可以用一次函数来表示（垂直于x轴的直线除外）。因此，一次函数与坐标平面上的直线就存在着某种对应关系，这种对应关系在其它函数中依然存在，我可以运用它解决有关问题。

例如2、李小明每月的费用是由他在家上个月的工作时间收入加上父母给的基本生活费用构成。如果李小明每月在家庭劳动时间是X小时，该月李小明将获得的总费为y元，则y（元）和x（小时）的函数关系式的图象如图所示。

（1）请根据所给图象，求出李小明每月的基本生活费是多少元；他的父母又是如何给李小明劳动奖励的？

（2）当0≤x≤20时，求函数解析式；

（3）若李小明5月份要有250元费用，则李小明4月份要做家务多少时间？

图1

分析：（1）根图象的信息，李小明每月的基本生活费为150元，他受到奖励方法是：若他的家庭劳动时间不超过20小时/月，可获得2.5元/小时；如果李小明在家庭劳动时间超过20小时/月，那么20小时内奖励不变,超过的部分可获得4元/小时；

（2）根据所给函数图象可知，当0≤x≤20时，可设函数图象的解析式为y=kx+b。由于点（0，150）与点（20，200）在函数y=kx+b图象上,可求得函数的解析式为y=2.5x+150；

（3）当x＞20时，根据函数图象可设y与x之间的函数解析式为y=kx+b。由于点（20,200）和点（30,240）在函数y=kx+b图象上,可求得函数的解析式为y=4x+120,当 y=250 时,即 4x+120=250,解得 x=32.5

由此可以看出，我们可以根据函数的解析式画出函数图象，同样也可以根据函数图象求出函数解析式，两者是一种对应关系。

三、以“形”求“数”，体验直观有效地解决问题

初中函数教学基本遵循这样的模式：实际问题分析特征得出函数概念，通过描点法画出图象，分析自变量值x的变化图象上点分布，x值的变化对点的运动趋势（图形特征），即对函数值y的正负与大小的影响归纳函数的性质（数量关系）。它指明了一种解决问题的方向：用代数运算的方法解决代数问题有时非常艰难，如果将代数问题转化为几何图形，观察其几何特征就可以得出代数结论，也就是说，代数问题不一定要运算才能得出结果，有时“看看”也可以求解.

例3、已知二次函数y=ax2+bx+c的图象与x轴的一个交点是A（4，0），对称轴为x=2，求关于的一元二次方程的解。

分析：要解决本道题，只要画一个简单的二次函数的图象。如图2，点A（4，0）是函数图象与x轴的一个交点，且对称轴为x=1，根据二次函数图象的对称性，则可求点B（-2，0）。所以，二次函数图像与x轴两个交点的横坐标就是方程ax2+bx+c=0的两个解，即x1=-2或x2=4。

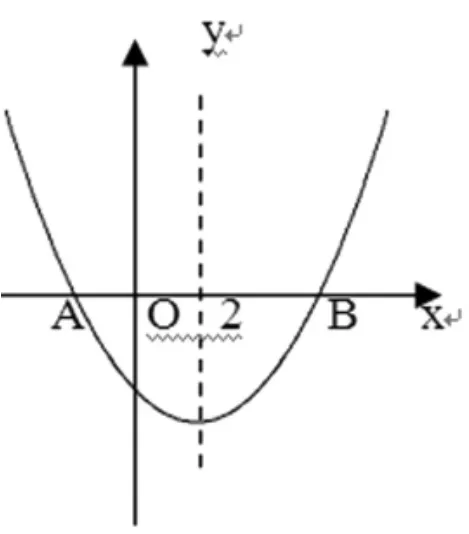
图2

四、以数求形，感受解决问题的乐趣

一般情况下，几何问题需要运用几何的定义、性质、公理和定理推理论证才能得出结论。由于初中学生知识面较窄，有的问题很难直接通过推理论证解决，特别是随着几何图形研究的深入，几何问题也越来越复杂，依靠几何方法往往难于入手解决。但是，如果有些问题具有函数背景或者是可以转化成函数问题，就可以运用函数图象计算得出几何结论。

例4、如图3所示，已知直线AD与坐标轴分别交于A、D两点，一次函数y-2x-1的图象与直线AD相交于点C，求直线AD、BC与y轴围成的三角形的面积。

分析：求三角形的面积需要知道三角形的一边的长和对应的高，从图形上看两个量都没有，我们只能另寻蹊径。注意到BC是一次函数的图象，直线AD经过二已知点A、D，对应的一次函数解析式可求，所以可以先求出C点和B点的坐标再求面积.

又BC对应的函数为y=2x+1②，

设点 C 的坐标为（xC，yC），则在①、②中，当 x=xC时，都有 y=yC，得

在 y=2x-1 中，令 x=0，则 yB=-1，

图2

在本题中求三角形面积所需的边长和高都不是根据三角形的几何性质求得，而是将问题转为求一次函数图像上点的坐标问题，利用坐标算出边长与高，这说明几何中有些证明类的问题照样可以通过计算得出几何结论。

例5、如图4所示，已知直线y=x+1与二次函数y=（x-1）2的图象交于A、B两点，M为线段AB上的一个动点（点M与A、B不重合），过M作MN⊥x轴，交二次函数的图象于点N点，E为对称轴与直线AB的交点，在线段AB上是否存在一点M，使得四边形CNME是平行四形？若存在，请写出点M的坐标；若不存在，请给出理由。

解：存在.设点M的横坐标为m，M、N两点的纵坐标分别为yM和yN。

∵ yM-m+1，yN=m2-2m+1

∴ MN=yM-yN-（m+1）-（m2-2m+1）=-m2+3m，其中0＜m＜3。

∵二次函数y=（x-1）2的对称轴为x=1，点E在直线y=x+1上，

∴ 点 E 的坐标为（1，2），则 CE=2。

要使四边形CNME是平行四边形，必需有MN=CE，即

∴-m2+3m=2，化简得m2-3m+2=0。解之得m2-1

当 m1=2 时，yM=2+1=3，yN=4-4+1=1，MN=-4+6=2，

当 m2=1时，yM=1+1=3，yE=1-2+1=0，点 N 的坐标为（1,0），与C点重合，

不合题意，舍去。

∵当m=2时，yN=1，yE=3，点N在点E的上方 ∴点P在线段AB上

∴当M（2，3）时，四边形CNME是平行四边形。

上述例子说明，要判断四边形DCEP是否可以是平行四边形，只要先算算PE是否能和DC相等，这样就先设点P的横坐标为m，用表示PE，再列方程求m，最后验证m是不是能m=2或m=1。整个解答过程都是计算，只用一个平行四边形的判定定理，说明“算算”也可以得出几何结论。

总而言之，引导学生运用数形结合思想去解决初中的函数问题非常重要，所以教师在初中函数教学中应有意识的强调与渗透，使知识与数学思想的教学融为一体，让学生更深入的掌握数学知识。教师只要认真备课，在具体的教学过程中精心组织课堂，对学生有目的地进行数形结合思想的渗透，并充分发挥学生的主观能动性，就能提高学生运用数形结合的思想去分析和解决问题的能力。