基于SV形态学方法的图像分解问题的研究

段 汕，谢长江，毛振帼

(中南民族大学 数学与统计学学院，武汉 430074)

最初的数学形态学方法主要采用固定结构元建立相关的形态学理论，但人们很快发现单一的固定结构元在实际应用中存在许多缺陷，由此结构元的自适应性研究成为改进这一问题的一个方向. 以Serra为代表的学者们[1-3]早在形态学建立初期就提出了结构函数的思想，将结构元视为空间位置变化的函数，Charif-Chefchaouni M和Schonfeld D等人在文献[4,5]中将其命名为空间变化(Spatially-Variant，简写为SV)的结构元(简称SV结构元)，并将固定结构元的形态学方法推广到SV结构元的情形[6]，对具有SV结构元的形态学(简称SV形态学，即Spatially-Variant Morphology)方法进行了一系列的研究，使得基于固定结构元的形态学理论得以推广.

图像分解与重构方法的研究是图像分析中的一个热点问题，有大量成熟的研究结果[7-9]. Xu J对基于骨架的图像分解及重构问题有一系列的研究成果[10,11]，其主要采用经典的数学形态学方法进行内、外骨架的提取，利用固定结构元的形态变换建立相关的图像分解及重构公式. Xu J在文献[12]中，将基于固定结构元的内、外骨架变换交替运用于图像的分解，得出了更为一般的分解算法，其优势在于它能够通过较少的骨架点构造出质量较高的近似图像. SV形态学方法的建立，使得对结构元的选取更具自适应性，结构元也从具体的形态变为更为抽象的空间变化的形式，这使得SV形态变换无论在理论上还是在实际应用中都更具优势，SV结构元的适当选取能更有效地实现对目标对象的相关处理. 鉴于SV形态学方法的这一特点，本文在Xu J关于骨架变换研究的基础上，将SV形态学方法应用于建立更具一般性的SV骨架变换，应用SV结构元及SV形态变换实现对目标对象基于骨架的分解和重构，最终获得的结果推广了已有文献的相关结论.

1 基础知识

关于SV形态变换，Bouaynaya N和Schonfeld D有较为系统的研究[5,6]，其中最为重要的内容之一，是将SV形态学中的SV结构元定义为一个由点到集合的映射θ：E→P(E)，其中P(E)为幂集，且SV结构元映射θ依继承序θ1≤θ2⟺θ1(z)⊆θ2(z)构成偏序集.SV结构元θ的转置结构元定义为：θ′(y)={z∈E:y∈θ(z),y∈E}.对于任意的X∈P(E)，4个最基本的SV形态腐蚀、膨胀、开、闭变换分别定义为：

(1)

(2)

γθ(X)=σθ(εθ(X))=∪{(θ(y)|θ(y)⊆X;

y∈E},

(3)

φθ(X)=εθ(σθ(X))={z∈E|θ(y)∩X≠∅,

∀θ(y)|z∈θ(y)}.

(4)

在以上定义的基础上，首先给出4个引理，作为后续工作开展的基础.

引理1 对于A,B∈P(E)，有σθ(A∪B)=σθ(A)∪σθ(B).

引理2 对于A,B∈P(E)，有εθ(AB)=εθ(A)σθ′(B).

引理3 对于SV结构元θ1和θ2，有σθ2(σθ1)=σσθ2(θ1)，即σθ2(σθ1)(X)=σσθ2(θ1)(X).

引理4 对于SV结构元θ1和θ2，有εθ2(εθ1)=εσθ1(θ2)，即εθ2(εθ1)(X)=εσθ1(θ2)(X).

2 SV的内骨架变换

利用SV开运算的非扩展性[5]，即γθ(X)⊆X，对X实施一次开运算γθ(X)，得：

X=γθ(X)∪S0=σθ(εθ(X))∪S0=

σθ(X1)∪S0,

(5)

其中X1=εθ(X)，S0=Xγθ(X).对X1作开运算γθ(X1)，将X1表示成如下形式：

X1=γθ(X1)∪S1=σθ(εθ(X1))∪S1=

σθ(X2)∪S1,

(6)

其中X2=εθ(X1)=εθ(εθ(X))=εθ2(X)，S1=X1γθ(X1)，将(6)式代入到(5)式，并利用引理1可得：

X=σθ(X1)∪S0=σθ(σθ(X2)∪S1)∪S0=

σθ2(X2)∪σθ(S1)∪S0=

σθ2(εθ2(X))∪σθ(S1)∪S0=

γθ2(X)∪σθ(S1)∪S0.

(7)

再对X2进行一次开运算γθ(X2)，将X2表示成如下形式：

X2=γθ(X2)∪S2=σθ(εθ(X2))∪S2=

σθ(X3)∪S2,

(8)

其中X3=εθ(X2)=εθ(εθ(εθ(X)))=εθ3(X)，S2=X2γθ(X2)，将(8)式代入(7)式，并利用引理1可得：

X=σθ2(σθ(X3)∪S2)∪σθ(S1)∪S0=

σθ3(X3)∪σθ2(S2)∪σθ(S1)∪S0=

σθ3(εθ3(X))∪σθ2(S2)∪σθ(S1)∪S0=

γθ3(X)∪σθ2(S2)∪σθ(S1)∪S0.

(9)

重复以上过程，最后可以得到如下公式：

X=σθn(Xn)∪σθn-1(Sn-1)∪σθn-2(Sn-2)∪…∪σθ(S1)∪S0=σθn(εθn(X))∪σθn-1(Sn-1)∪σθn-2(Sn-2)∪…∪σθ(S1)∪S0=γθn(X)∪σθn-1(Sn-1)∪σθn-2(Sn-2)∪…∪σθ(S1)∪S0,

(10)

3 SV的外骨架变换

关于外骨架，文献[12]中有明确的阐述，外骨架作为一种不同于内骨架的图像特征，在实际应用中有其特有的作用.

由SV闭运算的扩展性[5]，即X⊆φθ′(X)，对X进行一次闭运算φθ′(X)，有：

X=φθ′(X)T0=εθ′(σθ′(X))T0=εθ′(X1)T0,

(11)

其中X1=σθ′(X)，T0=φθ′(X)X，对X1作类似的操作得：

X1=φθ′(X1)T1=εθ′(σθ′(X1))T1=εθ′(X2)T1,

(12)

(13)

再对X2进行一次闭运算φθ′(X2)，并将X2表示成为：

X2=φθ′(X2)T2=εθ′(σθ′(X2))T2=εθ′(X3)T2,

(14)

(15)

重复相同步骤，最后可以得到：

(16)

4 内、外骨架统一的图像重构公式

以上分别利用内、外骨架给出图像的分解及重构公式，但单一运用内骨架或是外骨架进行分解往往产生大量的冗余，且骨架级数相对较高.文献[12]通过实例说明综合运用内、外骨架能重构出高质量的近似图像，且用于重构的内、外骨架成分相对较少.为此，以下将利用SV形态学方法，对文献[12]中的相关工作作进一步地推广.

4.1 近似公式的推导

在已建立的SV内、外骨架变换的基础上，利用得到的公式及结论，通过交替实施开、闭运算，建立基于内、外骨架的图像分解及重构公式.

首先对X进行一次开运算γθ(X)，将其表示为：

X=γθ(X)∪S0=X′∪S0,

(17)

其中X′=γθ(X)，S0=Xγθ(X).对X′进行一次闭运算φθ′(X′)，可得：

X′=φθ′(X′)T0=X1T0,

(18)

其中X1=φθ′(X′)，T0=φθ′(X′)X′.将(18)式代入到(17)式可得：

X=X1T0∪S0.

(19)

运用(7)式可以将X1近似地表示为：

(20)

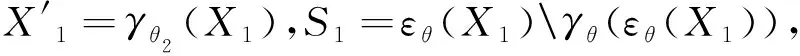
(21)

(22)

X≈X2σθ(T1)∪σθ(S1)T0∪S0.

(23)

最终可得X的两个近似表示式：

X≈Xnσθn-1(Tn-1)∪σθn-1(Sn-1)…

σθ(T1)∪σθ(S1)T0∪S0,

(24)

及

σθ(T1)∪σθ(S1)T0∪S0,

(25)

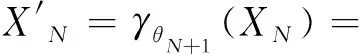
X≈σθN(SN)σθN-1(TN-1)∪σθN-1(SN-1)…

σθ(T1)∪σθ(S1)T0∪S0.

(26)

4.2 近似公式的证明

可以证明，以上所得到的关于X的所有近似表示式均为等式.下面在4.1节相关公式推证的基础上展开证明.

对第一个近似公式(21)式，由X′⊆φθ′(X′)=X1，开运算的增性[5]和(20)式知：

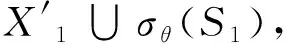
又X′=γθ(X)，根据开运算的等幂性[5]可得：

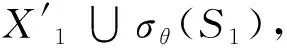
由X′=φθ′(X′)T0=X1T0知，X′不含有T0中任何点，故有

两边同时并上S0，利用(19)式，得：

(27)

这说明第一个近似公式(21)式的右边包含X作为子集.

对于第二个近似公式(23)式，根据(22)式及闭运算的扩展性[5]可知：

(28)

将(28)式带入到(27)式中，可得：

X⊆X2σθ(T1)∪σθ(S1)T0∪S0,

(29)

这说明第二个近似公式(23)式的右边包含X作为子集.

(30)

将(30)式代入到(27)式，可得：

(31)

这说明当n=2时，(25)式的右边包含X作为子集.

重复类似的推证，一般地可以得出(24)式及(25)式亦满足：

X⊆Xnσθn-1(Tn-1)∪σθn-1(Sn-1)…

σθ(T1)∪σθ(S1)T0∪S0,

(32)

…σθ(T1)∪σθ(S1)T0∪S0,

(33)

X⊆σθN(SN)σθN-1(TN-1)∪σθN-1(SN-1)…

σθ(T1)∪σθ(S1)T0∪S0.

(34)

由此证明了以上关于X的所有近似表示式的右边均包含X作为其子集.

为证明以上近似公式中的反包含关系亦成立，运用集合的补运算及开、闭运算的对偶性[5]进行相关推证.关于XC可以得出：

XC=(X1)C∪T0S0,

(35)

关于XC的一般形式的近似公式如下：

(X)C≈(Xn)C∪σθn-1(Tn-1)σθn-1(Sn-1)∪…∪σθ(T1)σθ(S1)∪T0S0,

(36)

(37)

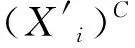
因而，在(37)式中，当n=1时，由闭运算的扩展性[5]可知：

结合(35)式也即：

(38)

这说明当n=1时，(37)式的右边包含XC作为其子集.对于(36)式，当n=2时，有：

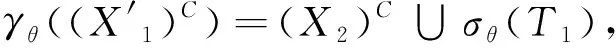
(39)

将(39)式代入到(35)式中可得：XC⊆(X2)C∪σθ(T1)∪T0S0,(38)式表明XC不含有σθ(S1)中的点，故：

XC⊆(X2)C∪σθ(T1)σθ(S1)∪T0S0,

(40)

这说明当n=2时，(36)式的右边包含XC作为其子集.对于(37)式，当n=2时，根据闭运算的扩展性[5]可知：

(41)

将(41)式代入到(40)式便可得：

(42)

这说明当n=2时，(37)式的右边包含XC作为其子集.

重复类似的推证，一般地可以得出(36)及(37)式亦满足：

XC⊆(Xn)C∪σθn-1(Tn-1)σθn-1(Sn-1)∪…∪

σθ(T1)σθ(S1)∪T0S0,

(43)

…∪σθ(T1)σθ(S1)∪T0S0.

(44)

XC⊆σθn-1(Tn-1)σθn(Sn)σθn-1(Sn-1)∪…∪

σθ(T1)σθ(S1)∪T0S0,

(45)

由此证明了X的近似等式的右边均是X的子集.综合以上的推证结果可知，4.1节中所有关于X的近似式均为等式，即一般地有：

X=Xnσθn-1(Tn-1)∪σθn-1(Sn-1)…

σθ(T1)∪σθ(S1)T0∪S0,

(46)

σθ(T1)∪σθ(S1)T0∪S0,

(47)

X=σθN(SN)σθN-1(TN-1)∪σθN-1(SN-1)…

σθ(T1)∪σθ(S1)T0∪S0,

(48)

(48)式给出了内、外骨架的SV形态骨架变换的推广形式.

5 结束语

本文将SV形态学方法应用于基于内、外骨架的图像分解及重构问题的研究，用SV结构元替代固定结构元，建立了SV形态学内、外骨架变换，将骨架变换推广到更为一般的形式，弥补了固定结构元对图像重构方法的局限性. 此外，本文还研究了将内、外骨架同时作为分解成分时的图像分解和重构问题，得到了SV内骨架变换和SV外骨架变换的一个统一形式，并给出了一系列相关的推算和证明. 本文就SV形态学方法在图像分解问题中所涉及的相关算法的理论框架进行了研究，后续工作将对所建立的各类图像分解算法进行实验分析，以完善我们的研究工作.