一般线性锥优化问题强锥对偶定理的新证明
(长江大学信息与数学学院,湖北 荆州 434023) (湖北省洪湖市第一高级中学,湖北 洪湖 433200)
线性锥优化是决策变量取自锥,约束函数和目标函数均为线性函数的一类优化问题的总称。作为凸优化的特例, 它始于Nesterov和Nemirovskii[1]的工作,主要包括线性规划、二阶锥优化和半定规划3种类型。后两种类型是线性规划在非线性优化领域的扩展,具有许多类似于线性规划的结构,实际应用非常广泛,例如线性锥优化在电气工程中的应用[2,3]、二阶锥规划在电气工程中的应用[4]、二阶锥规划在地质研究中的应用[5]、半定规划在信息与计算科学中的研究[6]。
对于一个已知的线性规划,总是可以求出它的对偶线性规划。当原问题不易求解时,寻找等价的对偶问题进行求解是一个不错的选择,这种选择的理论基础就是强对偶定理。近年来许多人对强对偶定理的研究做出了贡献;如余维等[7]研究了广义弧式连通凸锥优化问题的最优性条件及其对偶问题;罗丹和罗洪林[8]采用离散化方法证明了Lagrange强对偶定理。
一般线性锥优化问题和其对偶问题如下:
(1)
(2)
其中,A∈Rm×q;b∈Rm;c∈Rq;K和K*是Rq内一对互为对偶的正则锥。引用凸分析的一些基本概念和结果见文献[9~11]。
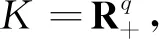
定理1[1]锥对偶问题(2)的目标最优值不超过原问题(1)的目标最优值。
1 预备知识
引理1[10,11](凸集分离定理)设S,T是Rq中2个具有非空相对内点的凸集,则S和T正常分离的充要条件是它们的相对内点的交为空,即:
ri(S)∩ri(T)=Ø
引理2(线性不等式组的选择定理)设A∈Rm×q,b∈Rm和c,λ∈Rq,μ,p∈R。如果存在点x0∈Rq满足Ax0=b和cTx0≤p,那么不等式组:
Ax=b
cTx≤p
λTx>0x∈Rq
(3)
无解的充分必要条件是不等式组:
ATy-μc+λ=0
(4)
bTy-μp≥0y∈Rmμ≥0
(5)
有解。
证明假定不等式组(3)有解,可证不等式组(4)、(5)无解。若不然,则存在y∈Rm和μ≥0满足式(4)和式(5)。在式(4)两边同时左乘xT,并利用不等式组(3)得到:
0=xT(ATy-μc+λ)
=(Ax)Ty-μcTx+λTx
≥bTy-μp+λTx
>bTy-μp
与式(5)矛盾。
若不等式组(3)无解, 则线性规划问题:
maxλTx
s.t.Ax=b
cTx≤p
是可行的且有上界0。应用线性规划强对偶定理[12,13],该问题的对偶问题是可解的,且对偶目标最优值小于或者等于0。
综上,引理2成立。
引理3[1]线性函数f(x)=cTx在凸集S的相对内点x*∈ri(S)取得最大值或者最小值当且仅当f(x)在S上恒为常数。
引理4是凸优化强对偶定理,即凸优化的Lagrange对偶无对偶间隙。
引理4[11]设f:Rq→(-∞,+∞]是正常凸函数,A∈Rm×q,b∈Rm。假定存在点x0∈ri(dom(f))使得Ax0≤b。如果优化问题:
(6)
有下界,那么相应的Lagrange对偶问题:
是可解的且对偶间隙为0。
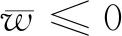
证明设τ*代表问题(6)的最优目标值,定义2个集合S和T:
T={(z,τ*)∈Rm×R|z≤0}
M={(Ax-b,τ)∈Rm×R|(x,τ)∈Epi(f)}
由引理1,存在非零向量(λ,β)∈Rm×R使得:
βτ*+λTz≤βτ+λTw∀(w,τ)∈S,∀(z,τ*)∈T
(7)
(8)
因为(0,1)∈Rm×R是集合S的回收方向,所以β≥0。此外,由x0是dom(f)的相对内点得到w0=Ax0-b是凸集D的相对内点,其中:
D={w∈Rm|∃τ∈Rs.t. (w,τ)∈S}
={Ax-b∈Rm|x∈dom(f)}
=A·dom{f}-b
如果β=0,在式(7)中令z=w0,可以得到:
由引理3 知,线性函数λTw在凸集D上取常数值,这与严格不等式(8)矛盾,因此β>0。
不妨设β=1,由式(7)得:
(9)
这里z≤0。容易验证λ≥0。若不然,则存在λ的某个分量λi<0,这时令zi→-∞(z的其余分量为0),则与式(9)矛盾。此外由式(9)还有:
=d(λ)
≤d*
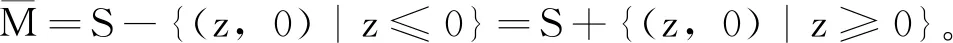
此外,注意到弱对偶关系τ*≥d*总是满足,因此有d(λ)=d*=τ*。于是对偶问题有解λ,从而结论成立。
值得注意的是,引理4的条件并不能保证问题(6)是可解的。如:
min ex
s.t.x≤0
是不可解的,但满足引理4的条件。
2 利用选择性定理改进的证明
与线性规划对偶理论不同的是,强锥对偶定理要求线性锥优化问题满足严格可行性,也称Slater条件。对于原问题(1)严格可行性要求存在x∈int(K)满足Ax=b;对于对偶问题(2)则要求存在y∈Rm满足c-ATy∈int(K*)。
下面是Nesterov和Nemirovskii[1]给出的强锥对偶定理,其证明过程也可以参见文献[14]。
定理2对于锥问题(CP)和它的对偶问题(D):
(1)如果锥问题(CP)下有界且严格可行,则对偶问题(D)可解,且p*=d*;
(2)如果对偶问题(D)上有界且严格可行,则锥问题(CP)可解,且p*=d*。
证明(1)假设锥问题(CP)下有界且严格可行,先考虑c≠0的情形。由假设,存在x0∈int(K)⊂Rq满足Ax0=b。定义集合:
U={x∈Rq|Ax=b,cTx≤p*}
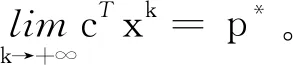
其次证明U∩int(K)=Ø 。若U∩int(K)≠Ø ,则存在点x1∈U∩int(K)使得cTx1≤p*。对于充分接近x1的点x,当然满足x∈int(K)。当c≠0时, 存在点x∈U使得cTx 由引理1,存在非零向量λ∈Rq使得: (10) 由此,线性不等式组: Ax=b cTx≤p* λTx>0 无解。由引理2知,存在y∈Rm和μ≥0使得: ATy+λ=μc (11) bTy-μp*≥0 (12) 下面用反证法证明μ≠0。若不然,则由式(12)得到bTy≥0。另一方面,将x0与式(11)两边作内积后可以得到: 〈λ,x0〉=-〈ATy,x0〉=-〈y,Ax0〉=-bTy 因为0≠λ∈K*和x0∈int(K) ,所以〈λ,x0〉>0,从而产生矛盾。于是有μ>0。 λ*∈K* ATy*+λ*=c 即(y*,λ*)是对偶可行的。另外由式(12)得到bTy*≥p*。结合定理1知,(y*,λ*)是对偶问题的最优解且d*=p*。于是结论成立。 对于c=0的情形,证明是平凡的。 (2)假设对偶问题(D)上有界且严格可行。这里证明大部分类似于(1),下面仅就不同的部分做简要说明。定义集合: V={c-ATy∈Rq|y∈Rm,bTy≥d*} 首先V≠Ø 和V∩int(K*)=Ø的证明完全类似(1)。 其次,由引理1,存在非零向量x∈Rq使得: 根据V的定义可得〈x,c-ATy〉≤0。于是对于半平面H={y∈Rm|bTy≥d*}的所有点y,有: (Ax)Ty≥cTx (13) 因为(Ax)Ty在半平面H内有下界,所以Ax与b只能成比例,即存在μ≥0使得Ax=μb(注意这里也可以仿照上面利用线性不等式的选择性定理)。 如果μ=0,那么由式(13)得到cTx≤0。另一方面, 由对偶问题(D)的严格可行性知存在y0∈Rm使得c-ATy0∈int(K*)。对充分接近y0的y∈Rm,也有c-ATy∈int(K*)。再由x∈K可以推得〈x,c-ATy〉>0,从而cTx>〈x,ATy〉=〈Ax,y〉=0。进而得到矛盾不等式0≥cTx>0,因此有μ≠0,亦即μ>0。 x*∈K Ax*=b cTx*≤bTy x*是原可行的且cTx≤d*。结合定理1知x*是原问题(CP)的最优解且p*=d*。 综上,定理2得证。 将锥对偶问题等价表示为Fenchel对偶形式,并以此为工具将凸优化的强对偶定理应用到锥上证明强锥对偶定理。 先考虑如下问题[15]: (14) 和其Fenchel对偶问题[15]: (15) 上述Fenchel对偶形式中,对偶函数仍然是采用Lagrange乘数法求得的,最终是利用共轭函数表示。 现在将一般线性锥优化问题(1)和它的对偶问题(2)转化为Fenchel对偶的形式,即: (16) 和: (17) 下面说明问题(16)、(17)与问题(1)、(2)等价的过程。 若x0∈Rq满足Ax0=b,N(A)代表矩阵A的核空间,即: N(A)={x∈Rq|Ax=0} 则问题(1)可以等价地改写为问题(16): 定义函数: 且假定E是q阶单位矩阵。易知函数f1和f2是凸的,进而求得: 因为c-λ∈R(AT),所以存在y∈Rm使得c-λ=ATy。同时左乘x0的转置后得到: (c-λ)Tx0=(Ax0)Ty=bTy 从而问题(17)可以等价地写成问题(2)。进而获得强锥对偶定理如下。 定理3如果问题(16)下有界,且存在x0∈int(K)满足Ax0=b,那么Fenchel对偶问题(17)是可解的且对偶间隙为0。 证明令: 满足引理4条件,于是相应的结果成立。 研究了一般的线性锥优化问题强对偶定理的证明,用2种方法重新证明了强锥对偶定理:用线性不等式的选择定理替代几何直观,克服了几何直观方法的特殊性;利用Fenchel对偶表示一般的线性锥优化问题,再利用凸优化的强对偶定理又一次证明强锥对偶定理。线性锥优化的理论研究上已经有了不少成果,但是半定规划和二阶锥优化新的理论证明及算法研究上,还值得进一步的探讨。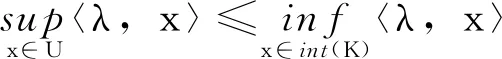
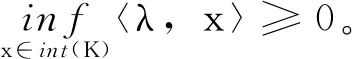


3 利用Fenchel对偶的证明
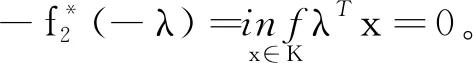
4 结语

