向量函数的泰勒公式的不同形式及其证明

◎胡有婧 (宁夏大学数学统计学院,宁夏 银川 750021)

1 引 言

数量函数的泰勒公式在数学中是一个非常重要的公式，有无数的研究成果.而对于向量函数的泰勒公式，中国知网能查到的文献并不多，微分几何教材中也只是给出了三维空间中带拉格朗日型余项的泰勒公式及其简略证明，本文参考文献[1]-[6]，给出了m维空间中向量函数的泰勒公式的不同形式与证明，希望对学习本部分内容和用到该公式的同志能有所帮助.

我们都知道，曲线和曲面的方程有多种形式，其中一种就是用向量函数来表示，而在微分几何、计算几何、计算机图形学、计算机辅助设计等课程中，所研究的起有着重要作用的曲线与曲面，也都是以向量函数的形式表示的，所以对它们的几何性质与逼近性质的分析，也是这些学科研究的内容之一.而向量函数的泰勒公式正是近似计算和理论探讨的有力工具之一，所以对向量函数的不同形式的泰勒公式的研究是非常有意义的.

本文中向量的坐标统一用花括号括起来，指标i的变化统一约定为i=1,2,…,m.

设V是实数域R上的一个m维向量空间Rm，I是V中一区域，如果对于每一点P(t)∈I⊂V，有一个确定的向量r(t)和它对应，则我们说，在I上给定了一个向量函数，记作

r=r(t)，P(t)∈I.

如果在V中取定坐标系，则向量函数对应的就有坐标，不妨设

r(t)={x1(t),x2(t),…,xm(t)}，

(1)

其中xi(t):R→R，均为I上的实函数.

2 向量函数的泰勒公式及证明

定理以t0、t0+Δt为端点的闭区间记作D，设向量函数r(t)在t∈D上有直到n+1阶的连续偏导向量，则有泰勒展开式

(1)拉格朗日型

(2)柯西型

存在0<θi<1，使得

(3)积分型

证明由已知条件和(1)式，易得分量函数x1(t),x2(t),…,xm(t)在t∈D上有直到n+1阶的连续偏导向量，根据数量函数的泰勒公式，得

(2)

其中Ri(t0+Δt)为余项，将(2)式代入(1)式，得

其中余项为

R(t0+Δt)={R1(t0+Δt),R2(t0+Δt),…,Rm(t0+Δt)}.

(3)

(1) 根据数量函数的泰勒公式的拉格朗日型余项，则存在

ξ1，ξ2，…，ξm∈D，

(4)

使得

(5)

将(5)式代入(3)式，得

(6)

根据向量函数的极限定义和运算法则，取极限可得

(7)

将(7)式代入(6)式得

(2) 根据数量函数的泰勒公式的柯西型余项，则存在

0<θi<1，

(8)

使得

(9)

将(9)式代入(3)式，得

(10)

再由已知条件和(8)式，得

所以

(11)

将(11)式代入(10)式得

其中

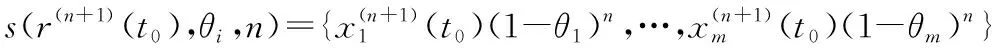
ε(t0,θi,Δt)={ε1(t0,θ1,Δt),ε2(t0,θ2,Δt),…,εm(t0,θm,Δt)}，

由(11)式得

(3) 根据数量函数的泰勒公式的积分型余项，得

(12)

将(12)式代入(3)式，根据向量函数积分的定义和运算法则得

当r(t1,t2,…,tn)是无限可导的，我们就可以把它展开为泰勒级数的形式， 即

如果r(t1,t2,…，tn)是解析函数，则上面的泰勒级数是收敛的[2].

3 结束语

对于三维空间中向量函数的带拉格朗日型余项的泰勒公式，在经典微分几何教材中有一个非常重要的应用，就是利用其对一般曲线在一点邻近的近似形状进行研究，得到曲线在一点的近似形状完全由该点的曲率和挠率确定，这在曲线论中也是一个非常重要的结论.对于m维向量空间V中的向量函数r=r(t)，它在V中所表示的几何图形仍然为曲线，此方程为其参数方程.利用本文中推导的定理，同样可以对其进行近似计算和代数逼近，得到相关的结论，感兴趣的同志可以自己去推导.