双边碰撞Duffing振子的对称性、尖点分岔与混沌*
李冠强 谢建华
(西南交通大学力学与工程学院,成都 610031)
引言
碰撞振动是工程和实际生活中一种常见的现象,碰撞导致系统具有强非线性、不连续性和奇异性[1,2].文献[3]研究了一类单自由度受简谐激励的对称碰撞系统,通过Poincaré映射和中心流形定理解析地分析了系统周期解的稳定性和局部分岔.文献[4]分析了受激倒摆与刚性固定壁碰撞振动系统的局部和全局分岔.文献[5]研究了一类单自由度双面碰撞振子的对称型周期n-2运动和非对称型周期n-2运动,通过分析对称系统Poincaré映射的对称性,证明对称周期运动只会产生音叉分岔,找到了系统通向混沌的路径.文献[6]研究了在双边约束的两自由度碰撞振动系统中,找到了由音叉分岔和周期倍化分岔通向混沌的路径以及对称和反对称运动的Hopf分岔.文献[7]研究了一类两自由度碰撞振动系统,通过计算系统Poincaré映射的线性化矩阵,确定系统的稳定性.文献[8]将OGY混沌控制方法应用到含双侧碰撞振动系统,把混沌控制到期望的目标控制轨道.由于以上问题都是分段线性的,可以求得系统的解析解进行分析.但是由于许多实际问题都是非线性的,难以求得其精确解,需借助近似解析方法和数值方法分析系统的动力学行为.文献[9]研究了具有刚性约束的n维非线性动力系统,通过几何方法推导了局部映射的Jacobi矩阵的解析式,给出了该类系统Poincaré映射Jacobi矩阵的计算方法.文献[10,11]借助非光滑的Melnikov方法研究了双边碰撞Duffing系统的动力学行为.文献[12]用改进的胞映射方法分析了双边碰撞Duffing系统的全局分岔和多解共存现象.文献[13]研究了冲击减振器与非线性能量阱(NES)耦合系统,数值模拟表明了该装置吸振效果的高效性.文献[14]分析了Duffing单边碰撞系统的混沌鞍.此外,文献[15]研究了动力系统的对称性.文献[16]将Duffing-Holmes系统离散为两维Holmes映射,运用中心流形定理分析了该映射的Pitchfork分支、Flip分支和Hopf分支.
本文考虑单自由度双边碰撞Duffing振子的对称系统和非对称系统,采用打靶法和不连续映射分析系统的周期解及其稳定性.数值模拟表明:随着参数的变化,对称系统通过音叉分岔产生两条具有相同稳定性的反对称周期轨道,观察到通过周期倍化通向混沌的路径.当参数发生非对称扰动时,系统中的音叉分岔过程产生了典型的对称破缺现象.
1 双边碰撞Duffing振子的运动微分方程
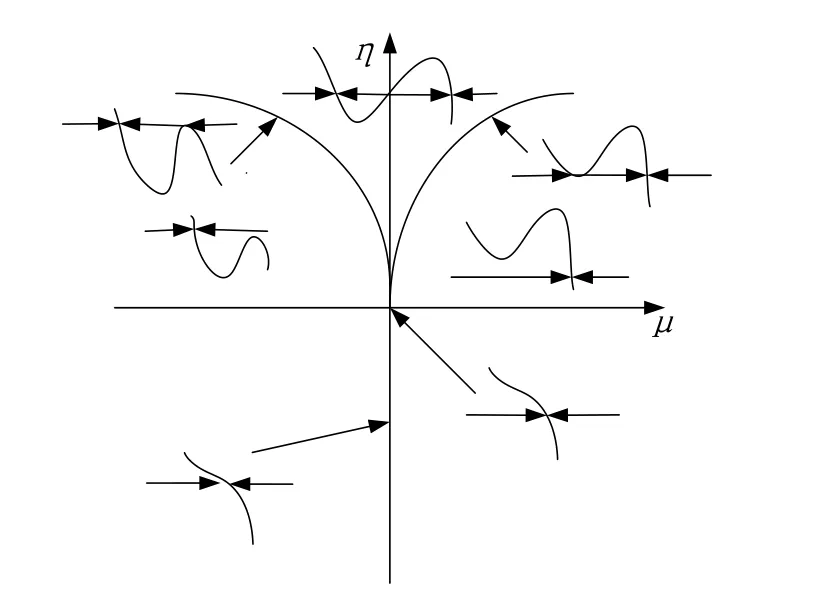
考虑单自由度双边碰撞的Duffing振子,在相邻两次碰撞间,即|x| 在一个周期T内,系统的双碰运动轨线如图1所示,假定振子先与右碰撞面发生碰撞.时间Poincaré映射在一个周期内可分为五个过程:(Ⅰ)A|→B:质量块从t=tA=t0到右碰撞面的过程;(Ⅱ)B|→C:质量块与右碰撞面发生碰撞的过程;(Ⅲ)C|→D:质量块与右碰撞面碰撞后运动到左碰撞面的过程;(Ⅳ)D|→E:质量块与左碰撞面发生碰撞的过程;(Ⅴ)E|→F:质量块与左碰撞面碰撞后运动到t=tF=t0+T的过程.那么这五个过程对应的映射可以表示如下: 图1 双碰运动的相轨线Fig.1 Phase portrait of double-impact motion 打靶法可以求得系统稳定的和不稳定的周期解.在给定精度的条件下,可以得到系统周期解比较精确的迭代初值,利用求得的初值直接数值积分可得到系统的周期解.另外,打靶法可求得Jacobi矩阵DP的特征值,如果所有特征值的模都小于1,周期解是稳定的;如果存在特征值的模大于1,周期解是不稳定的.在复平面上,当矩阵DP的模最大的特征值λmax以+1穿越单位圆时,系统的周期解可能发生音叉分岔、鞍结分岔或超临界分岔;λmax以-1穿越单位圆时,系统的周期解将发生周期倍化分岔;λmax以一对共轭的复特征值穿越单位圆时,系统的周期解将发生Hopf分岔. 对于非对称系统(r1≠r2),由于破坏了系统的对称性条件,则对称系统周期运动的音叉分岔将会演变为尖点分岔.对于对称系统r1=r2=r,取r和γ为控制参数,假定音叉分岔的临界值(r,γ)=(rc,γc),控制参数γ,使得η=γ-γc≠0,系统的周期解将会发生音叉分岔,此时对应的Jacobi矩阵的一个特征值以+1穿越单位圆,另一个特征值仍在单位圆内.对非对称系统,设r1=rc,r2=rc+μ.周期解的分岔可以用尖点分岔的两参数开折表示,如图2所示. 图2 μ-η平面上的尖点分岔Fig.2 Cusp bifurcation on the plane(μ,η) 令γ为控制参数,并取系统参数如下:a=-1,b=1,ω=1,β=0.2,r1=r2=0.8.当γ=0.64时,系统对应的Jacobi矩阵的两个特征值分别为λ1=0.851351,λ2=0.136931,因此对应的对称周期轨道是稳定的,系统的相轨线如图3(a)所示.当γ=γc=0.650526,此时Poincaré映射不动点的Jacobi矩阵的特征值λ1=0.999992,λ2=0.116577,此时的γc为音叉分岔的临界值.γ=0.73>γc时,通过音叉分岔形成两条反对称的周期轨道,这两条轨道具有相同的稳定性,对应Poincaré映射不动点的Jacobi矩阵的特征值λ1=-0.174665,λ2=-0.667428;同时对称的周期轨道失稳,对应Poincaré映射不动点的Jacobi矩阵的特征值λ1=2.09827>1,λ2=0.0555581,系统的相轨线如图3(b).当γ继续增加到γ=γd=0.741262,对应Poincaré映射不动点的Jacobi矩阵的特征值λ1=-0.999996,λ2=-0.116577,此时的γd为周期倍化分岔的临界值.当γ=0.75时,系统的相轨线如图3(c),两条反对称的周期轨道同时发生周期倍化. 图3 相轨线(一对反对称稳定的周期轨道(实线),不稳定的对称周期轨道(虚线))Fig.3Phase portrait(A pair of antisymmeric stable period orbits denoted by solid lines,unstable symmetric period orbit denoted by dashed line) 当γ继续增加时,系统通过周期倍化分岔通向混沌.当γ增加到γ=0.765时,Poincaré截面上各自生成两个离散的反对称的混沌吸引子,如图4(a).当γ=0.77时,两个离散的反对称的混沌吸引子各自融合成了一体,形成两个反对称的混沌吸引子,如图4(b)所示.当γ=0.78时,两个反对称的混沌吸引子演化为同一个对称的混沌吸引子,如图4(c). 图4 奇异吸引子的演变Fig.4 Evolution of chaotic attractors 图5给出了系统的全局分岔图,其中,图5(a)对应的初值为(0.05,0.5),图5(b)对应的初值为(0.4,1),图5(c)为(a)和(b)两种情况的组合. 图5 全局分岔图(PK:音叉分岔;PD:第一次周期倍化分岔)Fig.5 The global bifurcation diagram(PK:pitchfork bifurcation;PD:the first period doubling bifurcation) 如果改变恢复系数r2,使得r1≠r2,则对称系统变为非对称系统.与对称系统相比,由于不再满足对称性条件,在音叉分岔临界点附近的动力学行为发生了本质变化,系统对应的分岔图如图6所示,图6(a)反映了对称系统在音叉分岔附近的分岔图,然而,当r2=0.805≠r1时,音叉分岔过程演变为一支没有分岔的分支和一支鞍结分岔的分支,对应的分岔图如图6(b).图6(c)为对称系统和非对称系统两种情况的组合. 图6 从对称系统到非对称系统的演变Fig.6 Evolution from symmetric system to asymmetric system(SN:鞍结分岔,S:稳定的周期运动;US:不稳定的周期运动)(SN:saddle-node bifurcation,S:stable periodic motion;US:unstable periodic motion) 对于单自由度双边碰撞Duffing振子系统,分析了对称系统Poincaré映射的对称性,借助打靶法和不连续映射求得系统的周期解并分析其稳定性.对于对称系统,随着参数的持续变化,通向混沌的路径可以概括为:一个对称不动点→一对反对称不动点→一对反对称的混沌吸引子→一个对称的混沌吸引子.若r1≠r2,对称系统将演变为非对称系统,音叉分岔过程发生了典型的对称破缺现象,演变为两个相互独立的分支:其中一支没有发生分岔;另一支为鞍结分岔.
2 对称系统Poincaré映射的对称性


3 打靶法求系统的周期解



4 非对称系统的分岔
5 数值模拟
5.1 对称系统的分岔与混沌



5.2 从对称系统到非对称系统的演变

6 结论

