基于学生认知起点 培养数学运算能力

朱建玉

在小学数学中，乘法分配律是算术运算性质方面的重要内容，它联系了乘和加两种算术运算，贯穿了四则运算教学的全过程，可用于简算，而且与中学的因式分解内容联系紧密。乘法分配律内涵丰富，其表达式（a+b）×c=a×c+b×c，左边有两个运算符号（一个加号、一个乘号）和三个数，右边运算符号（两个乘号、一个加号）及数的个数（四个数），都发生了变化。如果重外形记忆，轻本质理解，那么学生受旧知的影响（如加法交换律、结合律以及乘法交换律、结合律，等式两边运算符号个数和数的种类与个数都是一致的），容易产生思维定势。应用时学生出错的现象特别多，经常出现这样的等式：a×（b+c）=a×b+c。教师往往花费大量的精力“纠错”，但收效甚微。要解决这样的问题，教师就应基于学生的认知起点，探索小学数学运算能力的培养策略，厘清算法背后的算理，促进学生思维发展，提升数学核心素养。

一、“形”“质”并举，关联建构

如何把人们在积累运算经验中归纳总结出来的静态结果变为动态表达？如何从本质上理解乘法分配律的内容是什么、为什么是这样的？我尝试将代数关系a×c+b×c=（a+b）×c巧妙地融合在两个矩形之间的面积关系之中，从“同数连加”的角度，借助乘法的意义、结合律、交换律得到分配律的表达式，在理解“分”与“配”的过程中，使学生感受数学知识中蕴含的内在逻辑推理。从单一的运算走向多维的运算，在教学中不仅要让学生掌握分配律的“形”，更要理解形背后的“质”，“形”“质”并举，关联建构。

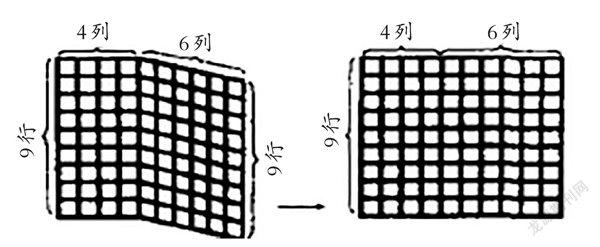
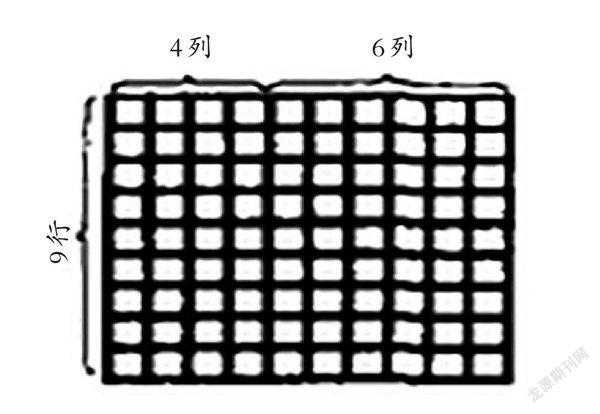
先出示“贴瓷砖”主题图：

提出问题：两面墙上一共贴了多少块瓷砖？

学生列出等式（4+6）×9=4×9+6×9。

师：两个不同的算式，结果却相等，你知道其中的奥秘吗？结合图形说说你的想法。

课件展示图形的动态变化，学生根据图形作出解释。

生：这两个算式的结果之所以相等，是因为这两个算式一个是把4列和6列合起来算，另一个是把4列和6列分开算。

生：我来补充，竖着看，一列有9块瓷砖，（4+6）×9先算4加6，共10列，（4+6）×9表示10个9相加。4×9+6×9是4个9加6个9，即4×9+6×9=9+9+9+9+9+9+9+9+9+9，也是10个9相加，所以结果相等。

师：你们都是这样竖着观察的吗（边说边用手圈出一个9）？如果横着观察，是否也能解释两个算式之间必然存在着相等关系？

生：如果横着观察，一行有1个4和1个6相配，9行是9个4和6的和，（4+6）×9是9个（4+6）。4×9+6×9是9个4加9个6，结果相等。

师：看来不管是竖着观察，还是横着观察，用乘法的意义都能解释为什么这两个式子存在相等关系。

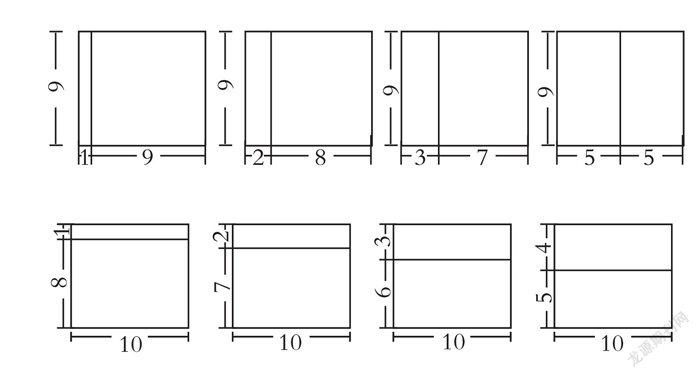
师：那上图中这个大长方形除了可以分成长9宽4和长9宽6的两个长方形外，还有其他的分拆方法吗？换一种拆分的方法，是否也存在等式？自己动手分一分，写出相应的等式。

生：我们是竖分的，又得到了四种分法，等式分别是（1+9）×9=1×9+9×9;（2+8）×9=2×9+8×9;（3+7）×9=3×9+7×9;（5+5）×9=5×9+5×9。

生：我们是横分的，得到四种不同分法，等式分别是（1+8）×10=1×10+8×10;（2+7）×10=2×10+7×10;（3+6）×10=3×10+6×10;（4+5）×10=4×10+5×10。

師：观察我们所写的这些等式的特征，你有什么发现？

生：这些算式都可以合起来算，也可以分开算。

生：等号两边的算式运算顺序不同，但结果相等。

生：无论是合起来还是分开算，得数都一样。

生：两个数的和同一个数相乘，可以用两个加数分别与这个数相乘，再把两个积相加，结果不变。

生：可以用字母表达（a+b）×c=a×c+b×c。

师：你们把这些等式的共同特征都用字母表达出来了。大家发现的这个规律是偶然的巧合还是必然的规律？

生：假设把墙面瓷砖分成a列和b列，每列c块瓷砖，两个式子都表示一共的块数，所以相等。

生：左边表示（a+b）个c，而右边是a个c加b个c，也是（a+b）个c，因此是相等的。

师：谁听明白了他要表达的意思？

生：我听明白了。这样的规律是一定存在的，我们可以借助刚才的长方形图来解释，两个小长方形的长分别是a、b，宽是c，那么大长方形的面积可以用（a+b）×c表示，也可以用a×c+b×c来表示，所以（a+b）×c=a×c+b×c。

师：真了不起，大家发现了数学上一个重要的运算定律——“乘法分配律”。

这样的教学不仅让学生掌握乘法分配律的“形”的特点，还让学生知道左右两边为什么相等，怎样转化，从而掌握乘法分配律的内在的“质”，在头脑中建立意义上的联系，做到有效建构，为正确使用打下坚实的基础。

二、变式训练，整体融通

四年级下学期，学生就已经学习了整数领域的乘法分配律，在开始学习小数和分数领域中的乘法分配律时，教材仅用了一个例题、一句“整数加法、乘法的运算律，对小数加法、乘法同样适用”作为具体内容。学习乘法分配律时，仅凭这种简单的语言和个别案例进行过渡的方式，学生很难实现思维从整数到小数和分数的迁移。如何帮助学生整体建构乘法分配律，让规律在不同的数领域灵活运用，是亟待解决的问题。

心理学研究表明，前面学过的知识会影响后面学习的知识，产生前摄抑制;后面学习的知识对以前学过的旧知也会出现倒干扰或者倒排斥，从而产生倒摄抑制。到了乘法分配律的推广阶段，学生已经学习了四则混合运算的运算顺序和所有的运算律及其运用，前摄抑制和倒摄抑制严重影响了学生合理、灵活地进行相关的运算。所以教师应充分考虑到这一点，要设计一些有针对性的辨错训练，帮助学生积累解题经验。

如5.4×0.9+0.1和5.4×（0.9+0.1）这两道题可帮助学生辨清：不能看到0.9和0.1能配成1就不顾运算顺序，盲目配成1。前面一题根本不符合使用乘法分配律的条件，并非所有的题都可以简便运算。125×4×25×8和125×8+25×4 这两道题可帮助学生辨清什么时候应用乘法结合律，什么时候应用乘法分配律。（27+[9/14]）÷9 和9÷（27+[9/14]）这两道题可帮助学生辨清什么时候可以直接把除法转化成乘法，不能一看到除号，就想直接转化成乘法。1.25×8÷1.25×8和1.25×8÷（1.25×8）这两道题则可帮助学生辨清除法性质的应用。

在辨错训练时，教师要根据学生的“最近發展区”，通过探索、求异的思维活动，使学生进一步理解运算律的真正含义，从而掌握简便运算的精髓。

三、保持敏感，洞察奥秘

教学中，学生学习了乘法分配律并且经常应用乘法分配律进行简便运算，熟练背出字母表达式之后，我发现并非每个学生都真正理解了乘法分配律。学生之所以在应用时出现这样那样的错误，究其根本原因就是对乘法分配律的理解并不透彻。

培养学生对算式认真观察的能力，提高对算式中一些数据的敏感性，区分一些易混淆的题目是提高学生简便运算能力的关键。所以，教师要有意识地帮助学生洞察算式的奥秘，使学生能灵活应用定律进行简便运算。我们要力争使学生在此过程中体会到简便运算的价值，把简便运算当做是自发需求，在此过程中碰撞出创造性思维的火花。

首先，要帮助学生学会熟练转化。整数运算律推广到小数和分数四则混合运算后，往往有学生一看见一道题目中既有分数又有小数或者百分数，就眼花缭乱。这就要求学生熟练掌握分数、百分数和小数之间的相互转化。一些常用的数据更须熟记于心。例如，0.25=[1/4]=25%，0.125=[1/8]=12.5%等。

其次，要帮助学生学会巧妙拆数。在简便运算中，学生经常出现拆数错误，因此在推广时对拆数的原则一定要进行复习。拆数一般使用加减乘法，运用加减法拆数一般应用乘法分配律，运用乘法拆数一般应用乘法结合律。拆数原则是拆数前后一定要保持相等，一般把一个约等于1或约等于整十整百的数拆成1、10、100加上或减去零头数。例如，10.1拆成10+0.1; 999拆成1000-1，等等。

最后，要帮助学生学会“一眼看穿”。125和8、25和4是非常特殊的两组数，遇上了要特别注意（当然0.125和0.8、2.5和0.04之类也同样）。只要题目中有能配成整十、整百、整千数的，小数能配成1或其它一些整数的，分数遇到同分母分数加减的或者除法改写成乘法后能约分的，都要引起高度重视，这往往就是解此类题的关键所在。

这些专项训练对培养和发展学生的求异思维、发散思维和逆向思维相当有益，能使学生全方位、多角度地思考问题。同时，这些专项训练也是提高数学练习效率的有效途径。只要教师充分发挥主导作用，引导学生总结并寻找解题突破口的方法，及时归纳题目的共性和异性，学生解题时就能融会贯通，触类旁通。

教师应该充分把握知识的“生长点”与“延伸点”，在课堂上对学生进行价值引导、智慧启迪和思维点拨，使学生不仅能正确、熟练地计算，还能根据题目条件寻求合理、简洁的运算途径去解决问题。

（责任编辑：杨强）