“美学”视角下解题教学的设计研究*——以两道数列高考题为例

权亭亭 李孝诚

(淮北师范大学数学科学学院,235000)

本文以两道数列高考题为例，对“美学”视角下解题的教学设计进行探究．

一、“数学美”的几种典型表现形式及教学价值

数学是一门自然科学,而美学是一门人文社会科学,看似毫无联系的两门学科,却彼此联系、相互贯通,构成一种“数学美”.数学与美是分不开的,“美学”早已作为数学研究的原则融入到数学中.

“数学美”的具体形式包括简洁性、和谐性、奇异性、对称性以及逻辑严密性等,也就是说,“数学美”是一种理性、具体、形象、生动的美.如果教师可以在课堂中合理运用“美学”讲授数学高考题,让学生感受到“数学美”,那么学生学习数学的兴趣将是稳定而持久的.

1.激发数学学习兴趣

心理学研究表明,学生对于美的各种形式的感受,会使得大脑迅速进入到兴奋状态,产生愉快的心情.如果在教学中灵活应用“数学美”,这将会使数学课堂气氛活跃,提高学生学习数学的兴趣.那么,如何将“数学美”的思想渗透于课堂中呢?这就要求教师做足课前准备,将数学与美学有机结合,深入探究“数学美”，将数学课堂教学过程设计为发现“数学美”,鉴赏“数学美”,创造“数学美”的过程,从而激发学生学习数学的兴趣.

2.培养学生创新能力

“数学美”的一个重要教学价值是培养学生创造美的能力.要通过引导学生并提示解决问题的思路,使学生发现美,进而启发学生选择合适的“数学美”的形式,关联问题中的数学要素,逐步引导出学生认知中的美,完成创造美的过程.这不仅可以提高学生的数学直觉能力,而且可以培养学生的创新能力.

3.提高解决问题能力

“数学美”是一种形象的美,比如处处对称的圆、稳定的三角形、永不相交的平行线等等.要尽可能地契合学生心理活动转承启合的环节发生数学知识,通过教学设计,达到透过学生的认知方式发生数学认识的目的[1].可以从数学知识、数学经验以及“数学美”多个方面引导学生,从审美的角度分析解题方法的优劣,以创造新的解题方法,使问题完美解决,从而提高学生解决问题的能力.

4.陶冶学生思想情操

在数学教学过程中,往往会强调解题的方法,其实就是数学的思想,数学思想蕴含在数学知识中.数学题目众多,学生不可能每个都掌握,因此,应传递数学思想,学生应做到举一反三.“数学美”作为一种数学思想发挥着潜移默化的作用,要对“数学美”有深刻的理解,将“数学美”与教学有机结合,联系实际进行探索,帮助学生深化对知识的理解,陶冶学生的思想情操.

二、几种典型的“数学美”

1.对称美

数学中存在许许多多的对称美,包括图形和数式的结构、数学的概念、函数的图象等等.例如“<,=,>”所连接的两边构成对称美的要素,在数式的结构中抽象出对称美,利用不等号的对称性,引导学生对称美的审美意向,发现左右两边结构不一致,从而想到解决问题的本质,就是要使左右结构保持一致,想方设法地将其中一边进行化简或计算,使问题得以解决.在这一教学过程中,要牢牢把握学生的心理内驱力,将数学的对称美渗入到学生的认知中.再如数学中成对出现的概念,增函数与减函数、奇函数与偶函数、收敛与发散等等,体现了由一般到特殊的演绎法和由特殊到一般的归纳法,可以将对称美的思想运用于数学概念的讲解,使学生深入理解数学概念,感受数学知识的乐趣.数学的这种对称美,不仅给人以视觉上的享受,更为解题提供有利的信息,有助于从创造对称关系上把握问题的整体性[2].

2.和谐美

格式塔心理学派的奠基人韦特海默在其著作《创造性思维》中论述了创造性思维的核心,他认为:“创造性思维的核心是思维者关注问题的整体,理解问题的内在结构,将部分看作整体,把握整体与部分之间的联系”.社会与自然总是想方设法地使自己成为一个和谐的整体,数学更是这样,因而反映到数学上则表现为数学的和谐美,即多样性的统一[3].在数学高考题中,命题者所给出的条件也不是杂乱无章的,是具有一定联系的,引导学生探究试题整体与部分的和谐联系，是解题的关键.

三、高考数学解题的教学设计示例

1.学情分析

以2021年高考全国乙卷文科第19题和2015年高考安徽卷理科第18题为例.在设计高考数学习题课时,需要厘清以下几个问题:首先,这两道高考题是否有讲解的必要?因为在高考冲刺阶段,时间是非常紧张的,如果教师在课前没有将高考题研究透彻,就拿到课堂上去讲授,这必定会事倍功半,影响课堂的效率;如果这两道高考题班上有85%的学生已经掌握,那么这道题也就没有讲解的必要.其次,“数学美”的思想是否适用于这两道题?因为“数学美”只是化繁为简的一种思想,不是所有的问题都可以通过“数学美”来求解的.第三,这两道题的难点在哪里?再者,学生的困惑是什么?根据对安徽省淮北市某中学的高三班调查发现,班级中只有5%的学生得到满分,因此,这两道题有讲解的必要.

2.解法分析

对参考答案进行分析,参考答案是借助猜想获取一个结论,再利用数学归纳法验证猜想,这种方法是可行的.但是这种解题方法很麻烦，在高考中,运用这种思路解题,学生一方面要对猜想的结论进行验证,另一方面又可能对自己的猜想产生怀疑,而且运用数学归纳法验证猜想需要进行冗长的计算.在这样的压力下,许多学生都出现困惑,影响情绪[4].对参考答案进行否定,这就需要找到一种不同于参考答案的解法,这种解法可以易于学生理解.

(1)对称美

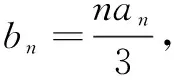
(1)求{an}和{bn}的通项公式;

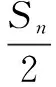
①

②

生1:①式是n项和,②式只有一项,故可以将① 式化简为一项,这样两边进行比较更容易一些.

师:比较两边的大小,需要将一边化简成一个具体的表达式进行比较.但是① 式并不是一个等差或等比数列,那么如何将① 化简为一项呢?

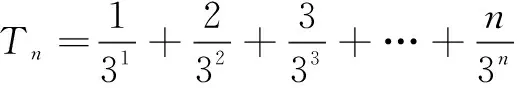
从“数学美”的形式看,不等号的对等性正是一种“对称美”的体现.在化简的定势思维下,学生可以想到将左右两边化简为形式结构相同的表达式,从而达到解题的目的.由此可以看出,数学中的“对称美”很好地使学生发现解决此类题型的思路.

(2)和谐美

师:给大家5分钟的时间思考一下这个题目,要证明不等式,能否通过将数量值放大或者缩小,将其变成一种相等的关系呢?(不等与相等两者之间是相对的),首先将不等式分成两部分

①

②

生1:我们想用放缩法对①式和②式进行放缩,可是①式过于复杂,是n项积,而②式只有一项,太简单.

③

④

式是一个整体,我不知道接下来该如何比较.

整个教学设计的过程意在促进学生产生“分项放缩”的数学观念,从“数学美”的形式看,将不等号通过分项放缩,直至放缩到相等,这正是一种“和谐美”的体现.在“和谐美”的审美意向指导下,将④式作为目标,通过分项放缩改变条件③的形式,把握整体与部分之间的联系,引导学生完成“完形”的心理内驱力.因此,在解题教学过程中,渗透“对称美”与“和谐美”的审美意向是非常重要的.在数学“对称美”与“和谐美”的审美意向的支持下,将难点一层层铺垫与展开,步步引导与启发,体现了教师在数学问题解决过程中处理问题的创造性[5].