奇偶对称是一家 图象平移可转化——对一道课本习题的教学探究

陶新芝

(江苏省昆山中学,215300)

课本中的例题和习题具有示范性和延展性,是训练学生思维,提升解题能力,培养数学学科素养的核心生长点．开展课本典型例、习题的探究性教学,有利于减轻学生的学业负担,有助于学生跳出题海．本文对一道课本习题的教学进行探究．

问题函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数,将其推广可得:函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

(1)求函数f(x)=x3-3x2图象的对称中心;

(2)类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是函数y=f(x)为偶函数”的一个推广结论.

一、课堂教学片断

1.巧用平移转化，探索问题解决

师:请从图象变换的角度说明推广结论中条件与结论之间的关系．

学生小组讨论结果:当a≥0,b≥0时，函数y=f(x+a)-b的图象向右平移a个单位,再向上平移b个单位,可得函数y=f(x)的图象;函数y=f(x+a)-b为奇函数,图象关于坐标原点对称,可推得函数y=f(x)的图象关于点P(a,b)对称.当a<0,b<0时,函数y=f(x+a)-b的图象向左平移a个单位,再向下平移b个单位,可得函数y=f(x)的图象;函数y=f(x+a)-b为奇函数,图象关于坐标原点对称,可推得函数y=f(x)的图象关于点P(a,b)对称.

师:函数y=f(x+a)-b为奇函数用符号语言怎样刻画?

生:f(-x+a)-b=-[f(x+a)-b]⟺f(x+a)+f(-x+a)=2b.

师:根据以上分析如何求解本题第(1)问?

学生小组讨论结果如下:

方法1(待定系数法)

设函数f(x)=x3-3x2图象的对称中心是点P(a,b),则函数y=f(x+a)-b=(x+a)3-3(x+a)2-b为奇函数.

由奇函数的定义可得(x+a)3+(-x+a)3-3(x+a)2-3(-x+a)2-2b=0，即

(6a-6)x2+2a3-6a2-2b=0.

故函数f(x)=x3-3x2图象的对称中心是(1,-2).

方法2(图象变换法)

因为y=f(x)=x3-3x2=(x-1)3-3(x-1)-2,所以y=f(x+1)+2=x3-3x.由于y=f(x+1)+2=x3-3x是奇函数，所以函数y=f(x)=x3-3x2图象的对称中心是(1,-2).

师:类比原题结论,完成第(2)问．

生:函数y=f(x)的图象关于直线x=a成轴对称图形的充要条件是函数y=f(x+a)为偶函数.

师:用符号语言刻画函数y=f(x+a)为偶函数.

生:f(-x+a)=f(x+a).

本题看似简单,若深入挖掘可以得到一些新的结论,进而拓展学生数学思维空间,激发学生数学学习的兴趣.

2.问题特殊化,探寻思维新生长点

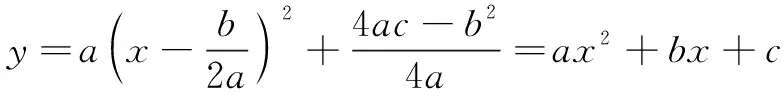
学生小组讨论结果:由三次函数y=f(x)=ax3+bx2+c+d是奇函数,图象关于坐标原点对称,猜测三次函数y=f(x)=ax3+bx2+c+d是中心对称图形,设对称中心为是点P(m,n),则f(x+m)+f(-x+m)=2n,代入f(x)=ax3+bx2+cx+d化简得：(3am+b)x2+am3+bm2+cm+d=n.由此可知

3.变换视角,拓展学生思维空间

师:若函数f(x)是定义在集合D上的奇函数,其图象关于坐标原点对称,若函数f(x)定义在集合D上且具有最大值和最小值,则f(x)max+f(x)min=0.类比推广,定义在集合D上的函数f(x)图象关于点P(a,b)对称,若函数f(x)是定义在集合D上具有最大值和最小值,则f(x)max+f(x)min=( ).

生:f(x)max+f(x)min=2b.

师:若函数f(x)是定义在集合D上的偶函数,其图象关于y轴对称,若函数f(x)在集合D上有奇数个零点,则有f(0)=0,类比推广,若定义在集合D上函数f(x)图象关于直线x=a对称,若函数D上有奇数个零点，则有( )：

生:f(a)=0.

4.学以致用,揭示高考题神秘面纱

(A)f(x-1)-1 (B)f(x-1)+1

(C)f(x+1)-1 (D)f(x+1)+1

例2(2017年高考数学课标Ⅲ卷理科)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( )

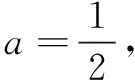
(A)0 (B)m(C)2m(D)4m

二、教学反思

1.钻研教材,充分挖掘例习题的育人价值

课本是教师上课之本,学生数学认知之本,也是高考专家命题之本.分析教材是教师进行教学设计的基础,是教师上课的前奏.对教材分析是否到位,不仅关系到能否发挥教材的作用,也会直接影响教师的课堂教学质量[1].教学中,应注重对课本例题和习题的开发利用,对典型的例题和习题进行挖掘、联想、推广、引申，得到综合性强、形式新颖的问题,训练学生数学思维的灵活性和创新性,提升学生数学学科核心素养.

2.教师主导,用问题激活整个教学过程

学生数学核心素养的发展需要通过教师组织教学活动来引领．在教学过程中，数学问题是学生思维的发动机,因此要用精心设计的一系列问题来引导教学进程．根据课程内容提出有研究价值的问题,问题的提出要以学生已有的活动经验和认知水平为基础,但不能仅靠回忆或复述就能解决,而要能引导学生对以往学习经验整合,启发学生对核心内容探究,引发学生深度思考,从而使学生积极主动地参与数学学习活动．

3.学生主体,在活动中提升数学学科素养

数学核心素养培养是能动的,是依赖于大脑机能而存在的,具有很强的主体性,他人无法替代．数学经验需要在数学活动中积累,数学能力需要在数学活动中发展．数学核心素养的养成,仅依赖教师讲授是不行的,更重要的是尊重学生的主体地位,依靠学生亲身参与数学活动,并在活动中认真思考．在教学活动中,要给学生足够的时间和机会进行自主探究、合作讨论和展示交流,让学生在数学活动中发挥主观能动性,在分析和探究中实现数学思维和数学学科核心素养的提升．