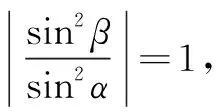关注热点 寻根溯源
——由一道新高考解析几何题引发的思考
刘达锋
(广东省广州大学附属中学南沙实验学校,511466)
本文从一道新高考解析几何试题出发,揭示命题背景,探究题源,挖掘命题的“题根”,达到由例及类、触类旁通的目的.
一、试题呈现

(1)求C的方程;

该题与2016年的四川高考理科数学第20题十分相似.

(1)求椭圆E的方程及点T的坐标;
(2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.
这两题第(2)问的条件类似,|TA|·|TB|=|TP|·|TQ|,|PT|2=λ|PA|·|PB|,容易让人想起初中所学的相交弦定理、割线定理、切割线定理.我们知道,椭圆是可以由圆伸长或压缩得到,那么,椭圆、双曲线是否也有类似定理?
二、寻根溯源
研究数学问题最好的方法也是寻根刨底,找到问题的根源.从基础入手,由浅入深,层层递进,找寻方法,挖掘真相.首先来看一下圆的相交弦定理的证明.
证明如图1,连结AD,BC,由圆周角定理的推论,得∠A=∠C,∠D=∠B.∴∆PAD∽∆PCB,∴PB∶PC=PD∶PB,PA·PB=PC·PD.
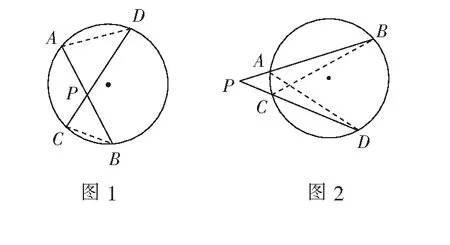
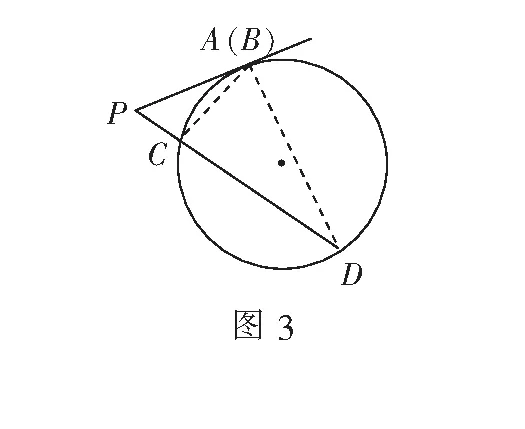
如图2,当点P在圆外时,就有了割线定理;如图3,当A,B重合一点时,有|PA|2=|PC|·|PD|,即切割线定理.
显然,想要通过相似三角形来探究椭圆的类似结论似乎不太可行;考虑通过弦长公式、距离公式直接运算求解,运算量又太大.那么还有没有更好的方法呢?说到长度距离问题,不得不说直线的参数方程是解决圆锥曲线中长度距离问题的最佳工具,不妨一试.
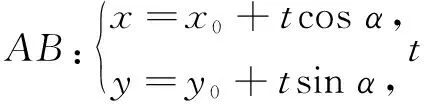
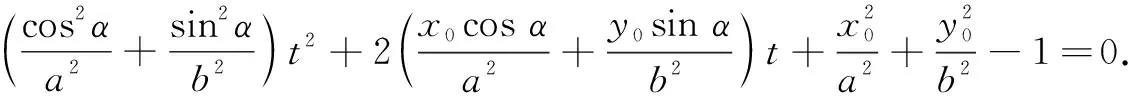
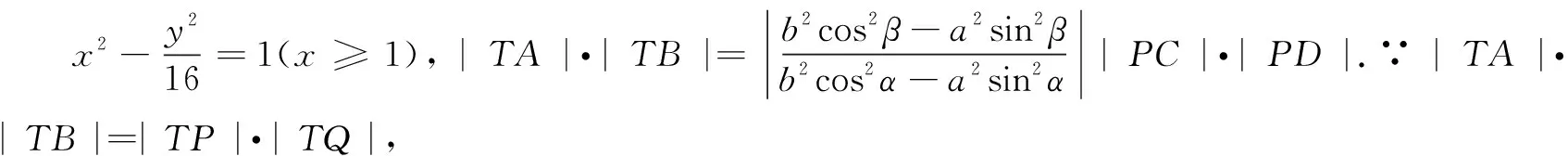
三、推广应用
设抛物线方程为y2=2px(p>0),过抛物线内一点P作两条直线与抛物线相交,交点分别为A,B和C,D,则则|PA|·|PB|和|PC|·|PD|有何关系?
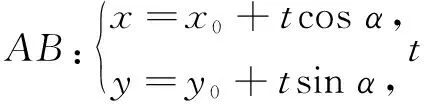
例3已知曲线C:y2=4x,倾斜角互补的两条直线l1,l2其中l1与曲线C交于A,B两点,l2与C交于M,N两点,l1与l2交于点P(x0,y0),求证:|PA|·|PB|=|PM|·|PN|.