基于门限分位数自回归模型的人民币汇率波动及预测研究

康 宁，刘 霆

（南京财经大学 经济学院，江苏 南京，210023)

汇率问题一直以来都是国际金融研究的热点话题。在经济生活中，汇率既与国家的宏观调控和经济政策等息息相关，又与国际经济稳定紧密相连，人民币国际化速度的逐步加快进一步影响了人民币汇率的波动频率和幅度。因此，需要准确、全面地分析人民币汇率的变化特征、预测汇率的波动趋势，为宏观经济政策的制定和调整提供科学合理的决策依据。

从现有文献中看，目前对于汇率波动及预测研究大致可以分为三类：一是基于线性均值框架下的建模方法。在线性均值框架下，建立ARMA自回归移动平均线性模型进行分析。例如，戴晓枫（2005）针对我国加入世贸组织后人民币对美元的日汇率值建立ARMA 模型，得到的最佳模型为ARMA（8,0）[1]。许少强（2007）运用ARMA 模型对一篮子货币欧元、日元进行汇率预测，并计算人民币汇率走势[2]。这种模型方法简单、方便操作，然而有着趋势单一，无法捕捉非线性关系的缺点。二是基于非线性均值框架下的建模方法。随着非线性模型的发展，越来越多的研究发现汇率变化更符合非线性波动的特征。国内学者使用平滑自回归模型（STAR），制度转换模型（R/S 分析方法）以及门限回归模型等方法对此开展研究。例如，靳晓婷（2008）通过门限自回归模型对2005 年汇改后的人民币对美元名义汇率进行研究，证实人民币汇率波动存在门限的非线性特征[3]。戎如香（2008）采用R/S 分析法对汇率的日收益率进行延及分析，表明人民币汇率具有非线性特征，其波动性存在明显的非周期循环[4]。张见（2012）运用双门限的SETAR 模型，分析汇率波动和调整速度的非对称特征[5]。王正新（2016）基于2005—2015年间的月度数据，采用平滑转移自回归（STAR）模型对人民币实际有效汇率（REER）波动的非线性机制进行分析和预测[6]。除上述三种结构化的非线性模型，Hua 等（2020）将神经网络模型应用于汇率预测，并得出神经网络模型预测能力优于尼尔森-西格尔回归模型和ARIMA 模型的汇率预测能力[7]。Liao 等（2020）利用BP 神经网络模型估计非线性残差，发现在汇率预测时组合模型优于单一模型[8]。以上基于非线性均值模型的人民币汇率研究结论虽然丰富，能够较好的解释汇率复杂变化趋势，但遗憾的是无法揭示人民币汇率的异质性特征、反映人民币汇率条件分布的完整信息。

第三类是基于分位数框架下异质性建模方法。Koenker 和Bassett（1978）提出的分位数回归为解决异质性问题提出了一个合理的方案[9]。Maik 等（2012）通过分位数回归模型研究了条件通胀分布在不同分位数下的通胀持续性的程度和结构稳定性[10]。Xu 等（2013）比较了线性分位数自回归（QAR）模型在金融动荡时期对四种每日股票指数回报的样本外预测表现[11]。Galvao 等（2009）利用门限分位数自回归模型研究美元/英镑汇率的动态，证实美元/英镑汇率回报相关存在重要异质性[12]。陈雄强（2013）运用分位数自回归模型研究中国通胀率的持久性及其非对称性特征，发现中国通胀率具有高持久性[13]。Karsten（2015）使用分位数自回归模型来估计残差过程的分位数依赖调整行为[14]。Konstantin（2018）通过分位数回归模型对美元即期汇率的日内动态进行了全面描述[15]。康宁（2017）在分位数回归框架下对上证综指日收益率进行实证研究，证实股票市场存在异质性特征[16]。以上研究表明，利用分位数回归模型研究金融数据异质性特征的国内外文献日益增多，但是关于人民币汇率的研究目前依然比较少见。

鉴于此，本文首次使用门限分位数自回归（TQAR）模型来研究人民币汇率的波动特征和趋势预测问题，主要创新工作包括以下两个方面：第一，门限分位数自回归模型集中了非线性的门限机制和异质性分位数回归建模的共同优势，能够更为贴切地刻画人民币汇率的复杂变化，揭示人民币汇率的非线性和异质性特征，得到优于传统模型的结果。第二，利用门限分位数自回归模型（TQAR）的预测技术，不仅能够给出人民币汇率的条件分位数预测、提高预测精准度，而且可以通过条件密度预测曲线，细致刻画出人民币汇率条件分布的完整信息。

1 模型与方法

1.1 分位数自回归QAR 模型

根据Koenker 等（1978）引入的分位数回归思想[9]，Koenker 和Xiao（2006）进一步提出了分位数自回归模型（QAR），该模型不同分位点处的自回归系数均是可变的，能够较为详细的刻画出模型在不同分位点的分布特征[17]。

对于时间序列{yt}，p 阶线性分位数自回归模型可以表示为：

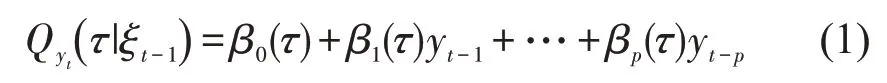
式中，ξt-1为直到t-1 时刻的信息集,τ(0＜τ＜1)为所选取的不同分位点，表示在τ 分位点处的条件分位数，βp(τ)为各分位点处的自回归系数。

该模型的参数估计可以利用数学规划法优化式（2）的目标函数获得：

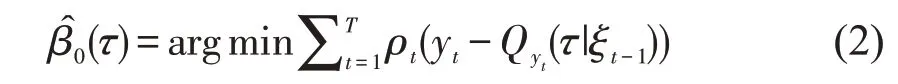
式中，T 为样本量。Koenker 和Xiao（2006），利用SIC 准则来确定模型的最优滞后阶数。

1.2 门限均值自回归TAR 模型

门限自回归模型是一类经典的非线性模型，最早由Tong（1978）提出，用以反映时间序列从一种机制跳跃到另一种机制的非线性行为特征[18]，Tasy（1989）进一步给出TAR 模型的建模及检验方法，此后TAR 模型在理论性质和实证应用方面得到了广泛的关注[19]。

一般地，对于满足k 机制门限自回归模型的序列{Xt}，TAR 模型可具体表示为：

其中，-∞=r0＜r1＜…＜rk-1＜rk=∞；rj表示门限值，j=1,2,…,k；k表示门限机制数，j表示第j机制；参数d为门限变量滞后阶数；{ξjt}是均值为0、方差为、独立的序列，且服从独立同分布。满足上述条件的模型通常记为：TAR(d,k,p1,p2,…,pk)。

当p1=p2=…=pk=p时，即模型满足在各机制的滞后阶数相等时记为：TAR(d,k,p)。

在实际应用中，Tong（1983，1990）提出TAR可以由不同状态下的AR(p)组成[20]。其中两状态的TAR 模型一般形式如（4）式：

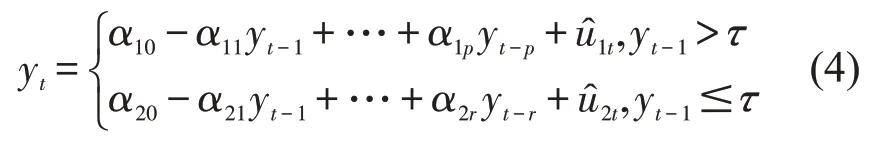
如果门限值已知，则根据yt-1的值是否落在相应门限值范围内来分离观测值。然后利用OLS方法分别估计每段模型，其滞后期长度p和r根据相应的AR 模型确定。若门限值未知，则采用网格搜索法，得到最优门限值τ和门限变量滞后阶数d的估计。

1.3 门限分位数自回归TQAR 模型

门限分位数自回归模型结合了门限机制和分位数自回归的共同优点，不仅能揭示数据的非线性，而且能兼顾数据的异质效应。Cai 和Stander（2007）基于贝叶斯方法提出自激励门限分位数自回归模型[21]，Galvao（2009）等利用门限分位数自回归模型研究美元/英镑汇率的动态[12]，Galvao（2011）等基于门限分位数自回归模型分析美国失业增长率[22]。目前，关于TQAR 模型的研究文献不多，特别是在中国金融经济数据中的应用较少，本文将以此为出发点进行研究。下面以二阶段门限分位数自回归模型（TQAR）为例，介绍其预测建模过程。

1.3.1 模型表示

假设时间序列{yt}为响应变量，{xi=(1,yt-1,yt-2,,yt-p)′} 为解释变量，{qt}为门限变量。建立模型如下：

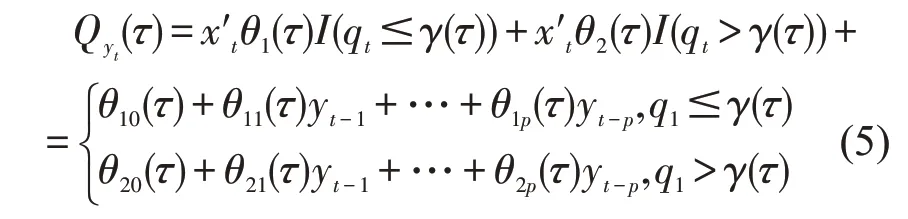
式中τ(0＜τ＜1)为分位点，I(·)为示性函数；γ 为门限值；θ 为门限回归系数。

1.3.2 参数估计

TQAR 模型的参数估计可通过下式（6）得到

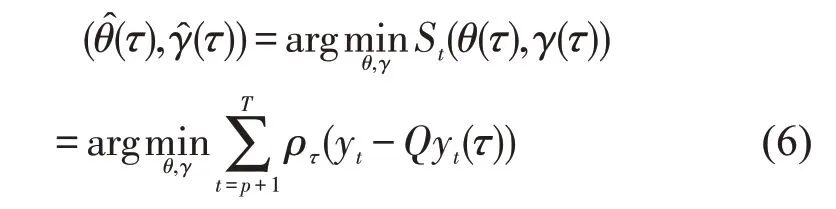
式中，T为样本量，p为滞后期，St(θ(τ),γ(τ))为目标函数。

1.3.3 模型定阶

根据康宁（2016）提供AIC 准则来确定最优滞后阶数p法[23]，具体公式如下：

式中前半部分代表模型的拟合程度；后半部分代表模型的复杂程度。

1.3.4 诊断检验

TQAR 模型的诊断检验，主要包括两方面：第一，门限效应检验，即检验模型是否存在非线性以及两机制方程的系数是否存在差异，本文采用SupWald 和AveAwald 检验统计量，用以检验TQAR 模型门限效应的存在性；第二，回归方程及回归系数显著性检验，本文采用似然比检验。

1.3.5 模型预测

在模型预测方面，TQAR 模型不仅能够实现点预测（即条件分位数预测），更重要的是能够提供条件密度曲线预测，从而细致刻画序列整个条件分布的完整特征。根据模型（5），在系数向量估计、门限值估计量的基础上，可以得到{yt}的条件分位数预测：

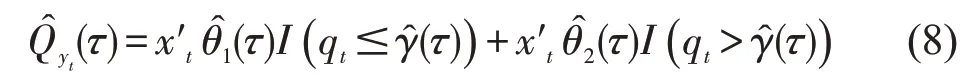
式（8）的自回归系数以及门限值随分位点而变化，从而{yt}实现条件分布预测。

在条件分布预测的基础上，进一步给出条件密度预测，具体公式如下：

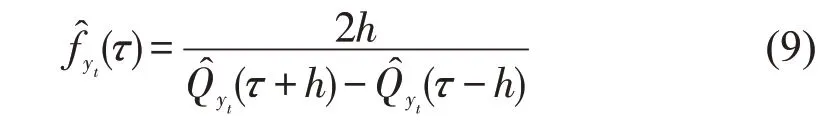
式（9）中，h表示窗宽，其最优选择标准参见Portnoy 等（1989）自适应核密度估计法[24]。

2 实证研究

2.1 数据来源

汇率是一项衡量宏观经济状况并为央行提供决策依据的重要指标，随着我国汇率体制改革的不断变化，人民币实际有效汇率由单方面升值的态势转为在一定区间内上下波动，对其波动的短期预测已成为一项重要课题。“8.11 汇改”作为人民币汇率结构性变化的一个重要分界点，研究其后续汇率的波动变化具有重要意义。因此本文选取2015 年8 月3 日—2021 年8 月6 日的人民币对美元中间价共1459 个数据进行分析，数据来源为国家外汇管理局。

下面将样本序列分为两个部分：2015 年8 月3 日至2021 年7 月30 日作为样本内训练数据，2021 年8 月2 日至2021 年8 月6 日作为样本外检验数据。首先针对训练数据进行描述性统计、平稳性检验，进而建立门限分位数自回归模型（TQAR）来研究汇率的波动变化特征，并与经典的线性时间序列模型（ARIMA）、门限自回归模型（TAR）以及分位数自回归模型（QAR）进行对比。最后研究人民币汇率的预测问题，利用检验数据来比较以上四种模型的点预测精度、评价其预测表现，并给出基于TQAR 模型的人民币汇率条件密度预测曲线。

2.2 描述性统计和平稳性检验

由图1 的人民币对美元汇率变化趋势来看，呈现阶段性贬值、过程中形成双向波动的趋势，并且逐步常态化。大致可以分为三个阶段，2015 年“8·11 汇改”至2016 年年末，人民币汇率基本呈单边贬值预期；2017 年人民币汇率呈阶段性升值预期；2018 年中美贸易摩擦开始、2019 年中美贸易摩擦升级、2020 年新冠疫情爆发等因素形成汇率双向波动趋势。

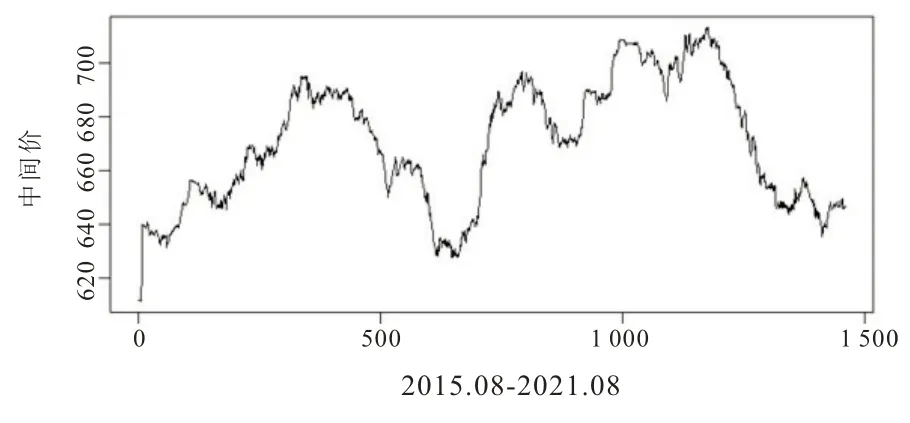
图1 人民币对100 美元汇率的时间序列图

下面采用迪基-富勒的ADF 方法检验人民币汇率序列的平稳性，发现检验p值为0.8903，大于0.05 的显著性水平，不能拒绝原假设，则汇率序列是非平稳的。因此需要对原始汇率序列进行对数差分处理，具体计算公式如下：

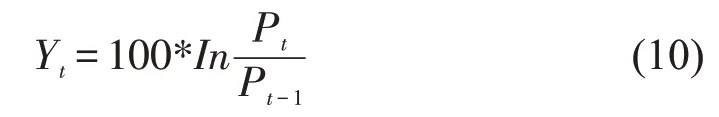
其中：Yt表示人民币兑美元汇率收益率，Pt为t日汇率中间价，Pt-1为t-1 日汇率中间价。

表1 报告了人民币对美元收益率的描述性统计和平稳性检验结果，其中汇率收益率均值是0.038，表明平均汇率收益率为0.038。偏度系数为正，说明汇率收益率序列为右偏分布，呈现非对称特征；超额峰度为5.841 大于0，具有典型的尖峰厚尾特征；此时的ADF 检验p值为0.01，说明经对数差分后的汇率收益率序列平稳。综合上述结论可以看出，人民币对美元汇率收益率具有平稳、非对称以及尖峰厚尾的分布特征。

表1 人民币兑美元汇率收益率描述性统计、平稳性检验

2.3 模型估计及检验

选取0.1，0.25，0.5，0.75，0.9 五个具有代表性的分位点，对样本内训练数据建立门限分位数自回归（TQAR）模型。由于偏自相关图显示一阶截尾，因此将门限变量设为滞后一期的汇率收益率，构建二阶段的TQAR 模型，其中阶段一（yt-1≤τ）表示人民币汇率波动较小阶段，阶段二（yt-1＞τ）表示人民币汇率受持续冲击波动较大阶段。同样利用该样本建立门限均值自回归（TAR）、分位数自回归（QAR）、线性ARIMA 模型进行对比。具体参数估计和诊断检验结果见表2、3 和4：

由表2 可知：TQAR 模型的门限效应检验（Supwald 检验和Avewald 检验）的p值为0，表明人民币汇率收益率存在显著的门限效应，同时LR检验表明五个分位点处回归方程均显著。表2 中TQAR 模型的参数估计结果显示，人民币汇率收益率序列存在典型的非线性特征和异质性特征，具体表现在：

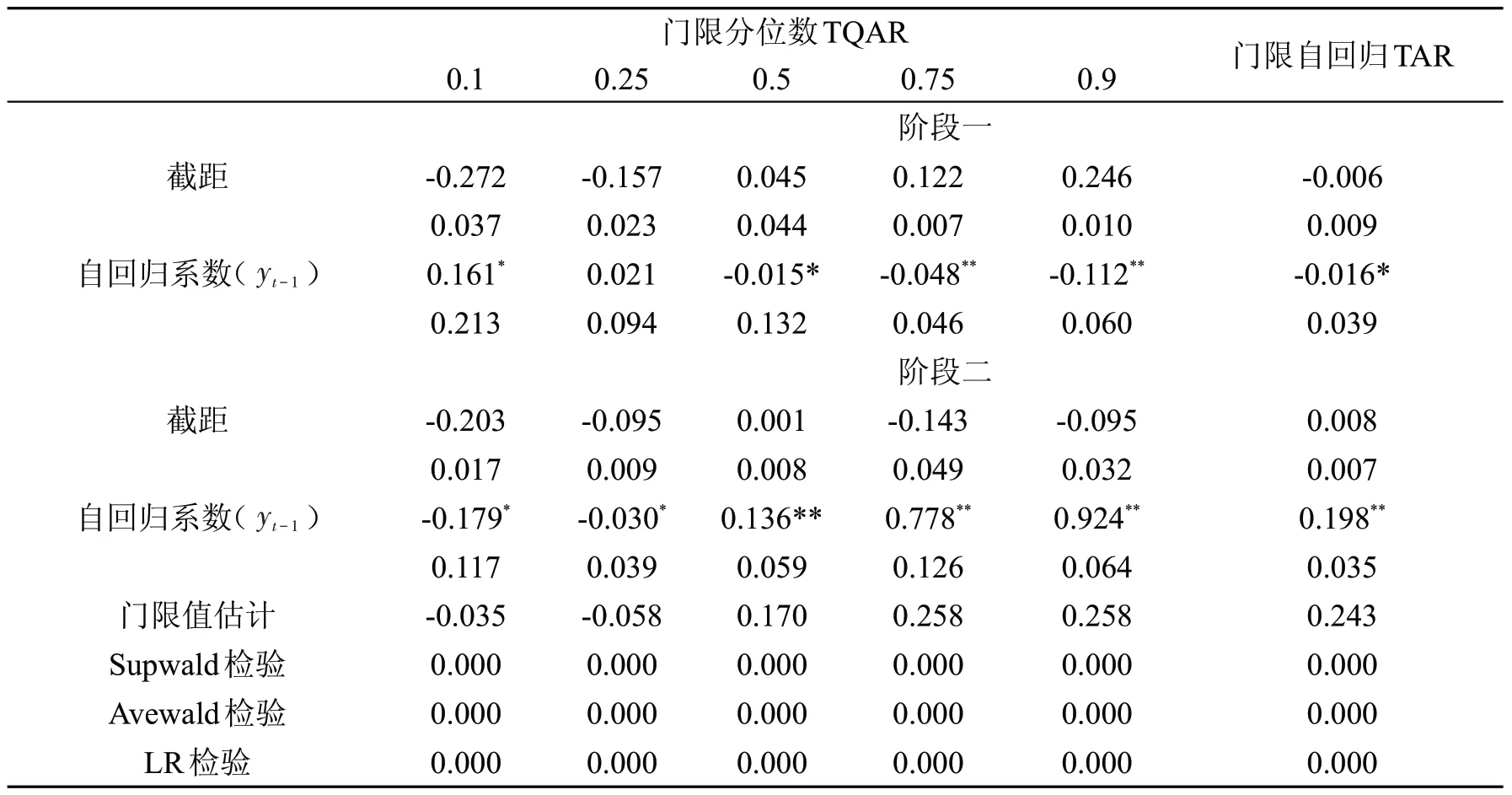
表2 TQAR 和TAR 模型参数估计及检验

第一，就人民币汇率的非线性特征而言，门限值估计将人民币汇率收益率的变化分为两个阶段，并且不同阶段收益率的波动路径差异较大。对于阶段1（yt-1≤τ），即人民币汇率波动较小阶段，在0.5、0.75 和0.9 三个分位点处门限自回归系数均小于0，这表明前期汇率收益率对当期呈现反向校正作用，前期汇率收益率越高，当期汇率收益率越低，具有一定向中心回复的趋势；在阶段2（yt-1＞τ），即人民币汇率受持续冲击波动较大阶段，可以看出，除0.1 和0.25 分位点之外，其余各分位点处自回归系数均为正数，且取值均大于第一阶段，这表明中高分位点处前期汇率收益率对当期具有正向影响且波动幅度较大，前期汇率收益率越高，当期汇率收益率越高。这一结论意味着，在阶段一汇率收益率波动较小，具有往均衡区域调整的趋势，因此可在适当时机进一步扩大波幅，提升人民币汇率的市场化水平；而在阶段二人民币汇率波动幅度大，汇率会出现大幅贬值或升值现象，往往会导致偏离均衡汇率较多，因此有必要保持流动性总量适度稳定，加快供给侧改革，避免汇率持续偏离。

第二，就人民币汇率的异质性特征而言，不同分位点处的自回归系数、门限值估计都存在差异，具体表现在：当yt-1≤τ时，汇率收益率序列在0.1分位点处自回归系数绝对值较大（系数为0.161），门限回归线较为陡峭，而其他分位点处的自回归系数绝对值较小，门限回归线较为平坦；当yt-1＞τ时，随着分位点增高，自回归系数取值逐渐增大，说明汇率收益率在低分位点的波动趋势相较于高分位点更加平缓。这一结果证实了，汇率收益率序列在不同分位点处的波动变化存在较大差异，具有明显的异质性特征。

此外，利用训练样本分别拟合TAR、QAR 以及ARIMA 模型，具体估计和检验结果见表2、3和4。由表2 可知，对于TAR 模型，模型门限效应显著，门限值估计为0.243，且各阶段回归系数均显著（10%水平），据此可将汇率收益率分为两个阶段，当（yt-1≤τ）表示人民币汇率波动较小阶段，自回归系数为-0.016，阶段二（yt-1＞τ）表示人民币汇率受持续冲击波动较大阶段，自回归系数为0.198。由表3 可知，对于QAR 模型，除0.9 分位点外，其余分位点处的自回归系数均显著（5%水平），自回归系数取值均为正，并且随着分位点的增加逐渐减小。由表4 可知，对于ARIMA 线性模型，自回归方程以及系数均显著（10%水平）；Ljung-Box 检验显示p值为0.987，接受不存在自相关性的原假设，说明残差为白噪声序列；White检验显示p值＜0.05，拒绝不存在异方差的原假设，说明模型中存在异方差。尽管上述模型从不同机制对人民币汇率收益率进行了拟合，但TAR模型仅能揭示汇率收益率的非线性特征，难以刻画汇率收益率的整个分布信息；QAR 模型虽能描述不同分位点处汇率收益率的异质特征，但无法揭示汇率收益率变化的非线性动态特征；传统ARIMA 线性模型存在异方差，效果劣于其他模型。比较而言，使用将门限机制和分位数回归相结合的TQAR 模型，能够更加细致地刻画出汇率收益率的复杂动态变化，充分揭示其非线性特征和异质性特征。

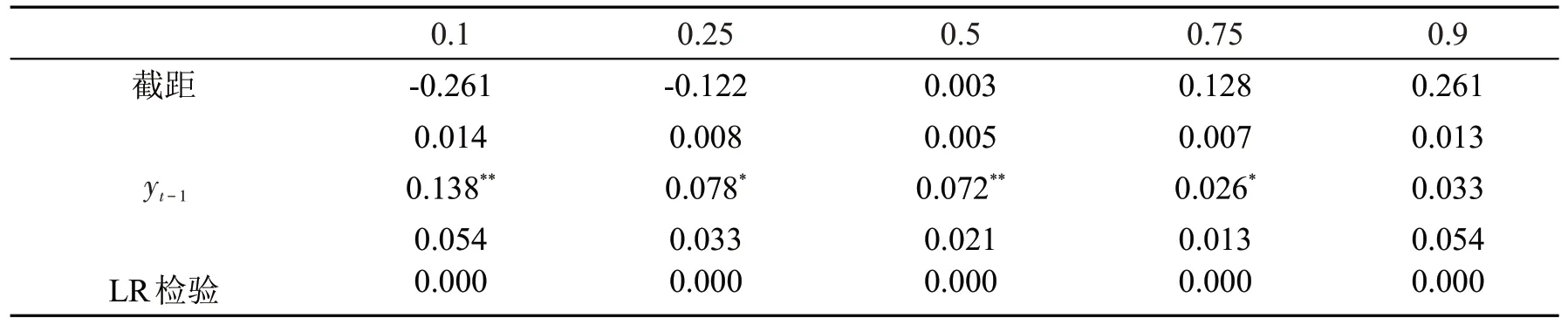
表3 QAR 模型参数估计及检验

表4 ARIMA 模型参数估计及检验

综上，基于TQAR 模型的人民币汇率收益率结论显示：不同分位点下汇率收益率波动特征存在差异，且模型两阶段自回归系数符号均不相同。这种不对称效应表明，在条件中位数以上的收益率，波动性和持续时间会愈加剧烈，而且这种效应在较高的分位数上得到增强。2015 年8 月11 日人民币汇率中间价改革，同时在此时期美联储加息预期，国内资本的大量流入，推动了人民币进入了一个相对较为显著的贬值通道。而随着个人购汇政策的颁布，人民币汇率开始双向波动并加快向市场化迈进的步伐，在2018 年全球经济复苏货币政策整体趋紧的大背景下，人民币汇率呈现总体贬值的态势，在2019 年中美贸易摩擦升级，2020 年新冠疫情爆发，2021 年新冠疫情防控成效以及相关疫苗的研发，多重因素促使着汇率呈现出双向波动的特征，充分体现了汇率收益率在各分位点阶段的变化特征。

2.4 汇改后人民币对美元汇率收益率的预测分析

在完成四种模型对训练数据的拟合后发现，TQAR 模型证实人民币对美元汇率收益率是非线性两阶段的，且在不同分位点处呈现出典型的异质性特征，相较于TAR、QAR 和ARIMA 模型所揭示的信息更为丰富。本节将从预测角度，进一步探讨TQAR 模型在人民币对美元汇率收益率预测方面的表现。通过选取预测绝对误差、均方根误差（RMSE）、平均绝对误差（MAD）三种指标，综合衡量TQAR 模型的预测能力，并与TAR、QAR和ARIMA 模型进行比较分析。

2.4.1 点预测及模型比较

利用2021 年8 月2 日至2021 年8 月6 日的样本外预测数据，分别使用TQAR、TAR、QAR 和ARIMA 模型进行5 步预测，并将得到的差分预测数据还原为原始人民币对美元汇率序列，具体结果如下：

表5 和表6 分别给出了基于TQAR 模型的人民币对美元汇率预测值和预测绝对误差值。可以发现，在大部分样本预测时期，0.5 和0.75 分位点处预测的绝对误差值较小，预测表现较好。根据前文的描述统计结果，人民币对美元汇率收益率数据为非对称序列、呈现右偏趋势，样本内估计结果也表明汇率收益率序列在TQAR 模型中高分位点处的估计结果与TAR 模型较为接近，因此下面选取0.5 分位点的预测结果与TAR、QAR 和ARIMA 模型进行对比。表7 报告了TAR、ARIMA 模型以及QAR 模型0.5 分位点处的预测结果，比较发现大部分样本预测时期TQAR 模型在0.5 分位点处的误差绝对值最小，TAR 模型次之，ARIMA模型和QAR 模型的预测表现相对较差。

表5 TQAR 模型的预测值

表6 TQAR 模型的预测误差绝对值

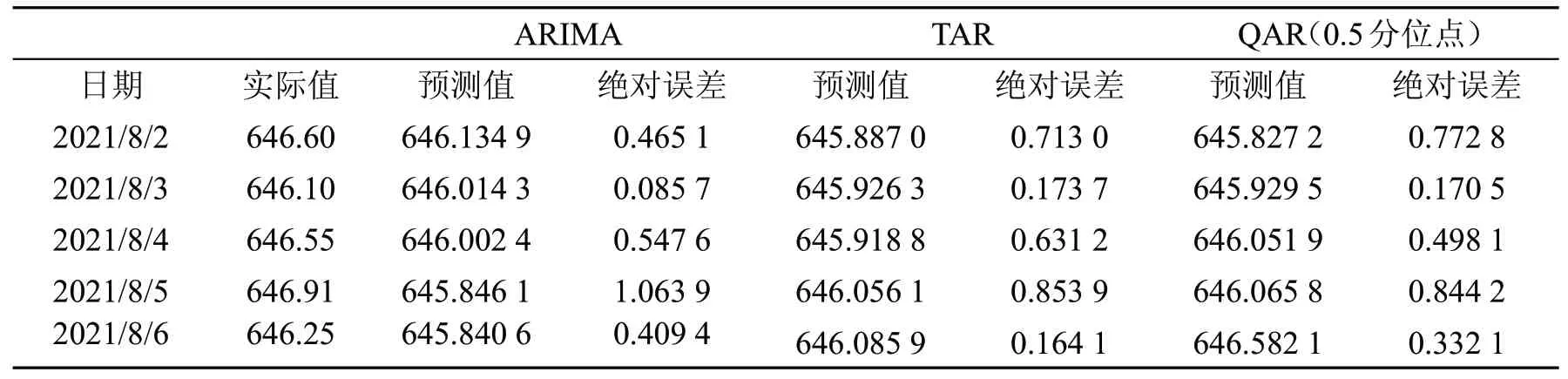
表7 ARIMA 模型、TAR 模型和QAR 模型的预测

进一步采用均方根误差（RMSE）与平均绝对误差（MAD）指标来评价四种模型的预测精度。从表8 中可以看出，TQAR 的预测效果总体上优于其余三种模型。TQAR 在0.5 分位点处的RMSE、MAD 指标值均小于ARIMA 模型、TAR模型和QAR 模型，其中RMSE 指标值相对于TAR、QAR 和ARIMA 模型分别降低7.97%、8.08%、11.31%，MAD 指标值相对于TAR、QAR 和ARIMA 模型分别降低了1.77%、3.29%、1.56%。从而表明TQAR 模型的预测精度最高，在点预测方面具有较好的表现。

表8 TQAR、TAR、ARIMA 和QAR 模型的预测精度比较

2.4.2 条件密度曲线预测

图2 报告了基于TQAR 模型的人民币对美元汇率收益率序列的条件密度预测曲线，可以看出，根据各期的条件密度预测曲线，能够得到人民币汇率收益率序列条件分布的全部预测信息，更好地揭示了各期汇率收益率序列的对称性、偏度、峰度等特征。此外，反映各期汇率收益率真实取值的实线，都落在条件密度预测曲线的最大可能区域内，并且与0.5 分位点预测的虚线较为接近，从而表明TQAR 模型不仅能够通过条件密度曲线获得更丰富的预测信息，而且以较大的概率做出准确预测。

图2 基于TQAR 模型的汇率收益率条件密度曲线预测

3 结论

随着汇制改革进程加速，对人民币汇率的研究不断深入，需要充分考虑汇率的复杂变动特征，从而更为准确、全面地实现对汇率波动趋势的刻画以及预测。本文首次利用门限分位数自回归模型（TQAR）研究“8.11”汇改后人民币汇率的波动趋势及预测问题，揭示人民币汇率的非线性特征和异质性特征，并通过与传统TAR、QAR 和ARIMA 模型对比，发掘TQAR 模型在人民币汇率波动特征及预测方面的优势。本文的主要结论包括以下两个方面：

首先，在波动趋势方面，TQAR 模型证实了人民币汇率波动存在显著的门限效应和异质效应。具体而言，第一，门限效应将汇率收益率划分为两个阶段，其中阶段一为人民币汇率波动较小阶段，前期汇率收益率对当期汇率收益率总体上影响较小；阶段二为人民币汇率受持续冲击波动较大阶段，此时前期汇率收益率对当期汇率收益率的影响较大，表现与阶段一相反。第二，异质效应表明不同分位点处的人民币汇率波动存在较大的差异，尤其在高分位点处与低分位点差异更为明显。这一现象意味着汇率收益率在不同的分位点处不仅受到前期汇率收益率的影响，具有一定的惯性效应，而且其影响程度随分位点的变化而变化，导致人民币汇率波动存在复杂的异质特征。其次，在预测能力方面，TQAR 模型能够较好地预测人民币汇率的变化趋势，不仅能够提供比传统的TAR、QAR 和ARIMA 模型更高的预测精度，而且能够通过条件密度预测曲线，细致刻画出人民币汇率条件分布的形状、位置和散布等全景信息。

根据上述结论，TQAR 模型能够较好地揭示人民币汇率变化的非线性及异质性特征，有助于把握汇率的短期波动规律，为根据汇率水平的高低预测未来走向提供了实证基础。在汇率波动较小阶段，由市场决定人民币汇率，因此可在适当时机进一步扩大波幅，提升人民币汇率的市场化水平；而在持续冲击波动较大阶段，汇率会出现大幅贬值或升值现象，往往会导致偏离均衡汇率较多，此时需要国家制定相应的宏观调控政策，进行适度引导和干预，以更好地降低风险。