基于直观想象 多维构造解法
魏宇亭


[摘要]中考试题,既要考查學生“四基“四能”的掌握情况,更应考查学生数学素养的发展状况.文章以2021年徐州市中考数学试卷第21题为例,从试题命制和批改等角度,论述培养学生以直观想象为代表的核心素养的教学启示.
[关键词]数学核心素养;直观想象;多维解法
《普通高中课程标准(2017年版)》指出:直观想象是指借助几何直观和空间想象感知事物的形态和变化,利用空间形式尤其是图形,理解和解决数学问题的素养[1].从定义上看,该素养主要涉及几何直观和空间想象两个方面.孔凡哲和史宁中教授指出,几何直观是在直观感知的感性基础之上所形成的理性思考的结果,是学习者对数学对象的几何属性的整体把握和直观判断的能力[2].可见,几何直观是解决数学问题的思考途径,能帮助学生认清问题的实质,理清解题思路,探索解题方向.笔者参加2021年徐州市中考数学试卷命题,随后负责第21题的批阅与仲裁,该题既考查了学生对三角形、平行四边形、圆等基本图形性质的综合应用,又从直观识图和优选解法两个角度考查了学生以直观想象为代表的数学核心素养的发展状况.现就该题的命制设想、基于直观想象的多维解法及批改中发现的典型错误,浅谈对教学的启示.
试题及出处
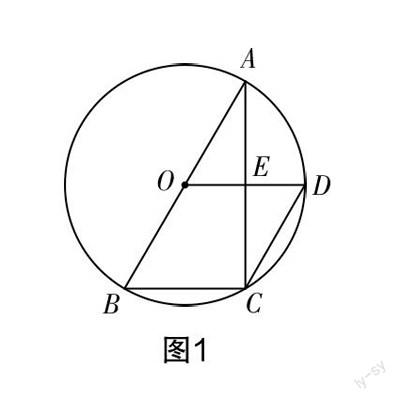
试题如图1所示,AB为⊙O的直径,C,D两点在⊙O上,AC与OD交于点E,AE=EC,OE=ED,连接BC,CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
【出处:2021年徐州市中考数学试卷第21题.】
命题设想
1.简而不庸,突出考查学生的直观想象素养
本题是一道基础证明题,设计该题时,旨在将三角形、平行四边形、圆等基本图形融入一题,提高试题的综合性和各知识间的关联度,且在构图上追求简洁、形态美观,所给条件明确,利于学生基于直观想象顺利解题.在图形的选择上,题中三角形和平行四边形均为特殊图形,具有特殊性质,内涵丰富.特殊图形的综合,图形特性的杂糅,为学生铺设了多维的解题思路,也制造了优选解法的挑战,能突显出学生以直观想象为代表的核心素养的发展状况.图形中含有30°、60°、90°和120°的特殊角,也预设了运用“数形结合”思想的解题条件,拓宽了解题思路,所以本题虽简单但不平庸.
2.多维解法,突出考查学生的逻辑推理素养
章建跃博士曾指出“推理是数学的命根子”.可见培养学生的逻辑推理能力在数学教学中的重要性.学生的逻辑推理能力是中考命题的重要考查点,本题很好地体现了相关的考查要求.在设问上,第(1)问证明两个三角形全等,第(2)问证明四边形为菱形,这两个结论的证得,均建立在严谨推理的基础上.学生对图形性质的熟悉程度,对符号语言的规范使用,以及对逻辑结构的严谨架构,是决定本题高质量完成的重要因素.题干与设问层次分明,两问之间的连续性强,两个问题步步拔高,层层递进,第(1)问的结论恰是第(2)问的条件,突显了命题的整体性、连续性和有效性.数学各核心素养不是孤立存在的,本题完美地体现了直观想象和逻辑推理之间的递进关系.如求证第(1)问,学生在直观想象的基础上会产生两种思路,其一,基于图形直观,易发现∠AEO与∠CED是一组对顶角,结合已有条件,易构成“SAS”的条件,从而完成求证;其二,根据已知条件“AE=EC,OE=ED”,基于直观想象,易发现连接OC,AD后所形成的四边形AOCD为平行四边形.虽然思路二略显笨拙,但也是学生基于直观想象的收获,应被认可.学生在直观想象的基础上确定求证思路,用规范的逻辑推理过程完成求证,能实现数学核心素养间的传导和综合应用.
试题多维解法荟萃
1.对于第(1)问,基于直观想象的求证思路分析
【维度1:基于对顶角相等的直观想象】
如图2所示,根据题干条件“AC与OD交于点E”,学生基于直观想象,运用对顶角相等的性质,易得∠AEO=∠CED,再与题干条件“AE=EC,OE=ED”组合,由“SAS”可得△AOE≌△CDE.
【维度2:基于发现平行四形AOCD的直观想象】
如图3所示,根据题干条件“AE=EC,OE=ED”,连接OC,AD后,可证得四边形AOCD为平行四边形.于是可得AO=CD.再根据“SSS”可得△AOE≌△CDE.
2.对于第(2)问,基于直观想象的多维证法赏析
试题汇聚了含30°角的直角三角形、菱形、圆等特殊图形,基于直观想象,第(2)问可产生多维解题思路.笔者整理后,绘制了如图4所示的解题路径图.可见,在多维的求证思路中,简捷与繁杂共存.解题时,学生要甄别优选,这能在高阶思维层面培养学生运用直观想象优选对象的素养.
【维度1:用定义法证明四边形OBCD是菱形】
证法1因为△AOE≌△CDE,所以OA=DC,∠OAC=∠DCE.所以AB∥CD.因为A,B两点在⊙O上,所以OA=OB.所以OB=DC.所以四边形OBCD是平行四边形.因为B,D两点在⊙O上,所以OB=OD.所以平行四边形OBCD是菱形.
证法3因为△AOE≌△CDE,所以∠OAC=∠DCE.所以AB∥CD.如图5所示,连接OC.因为A,C两点在⊙O上,所以OA=OC.又因为AE=EC,所以OE⊥AC,即∠AEO=90°.因为AB为⊙O的直径,所以∠ACB=90°.所以∠AEO=∠ACB.所以OD∥BC.所以四边形OBCD是平行四边形.因为B,D两点在⊙O上,所以OB=OD.所以平行四边形OBCD是菱形.
【维度2:构造“对角线互相垂直的平行四边形是菱形”的判定条件】
证法4如图6所示,连接OC,AD,因为△AOE≌△CDE,所以OA=CD,∠OAC=∠DCE.所以AB∥CD.所以四边形OCDA为平行四边形.因为A,C两点在⊙O上,所以OA=OC.所以平行四边形OCDA是菱形.所以∠OAD=∠OCD.因为OA=OB,所以OB=CD.又AB∥CD,所以四边形OBCD是平行四边形.所以∠CDB=∠ABD.连接BD交OC于点F.因为AB是⊙O的直径,所以∠ADB=90°.所以∠ABD+∠OAD=90°.所以∠OCD+∠CDB=90°.所以∠DFC=90°.所以OC⊥BD.所以平行四边形OBCD是菱形.
【维度3:构造“四條边相等的四边形是菱形”的判定条件】
OA=OB.因为B,D两点在⊙O上,所以OB=OD.所以OB=BC=CD=OD.所以四边形OBCD是菱形.
证法8如图8所示,连接OC,AD.因为△AOE≌△CDE,所以OA=CD,∠OAC=∠DCE.所以AB∥CD.所以四边形OCDA为平行四边形.因为A,C两点在⊙O上,所以OA=OC.所以四边形OCDA是菱形.所以OA=AD.因为A,D两点在⊙O上,所以OA=OD.所以OA=OD=AD.所以△AOD为等边三角形.所以∠AOD=60°.因为OA=OC,AE=EC,所以OE⊥AC,即∠AEO=90°.因为AB为⊙O的直径,所以∠ACB=90°.所以∠AEO=∠ACB.所以OD∥BC.所以∠B=∠AOD=60°.因为B,C两点在⊙O上,所以OB=OC.所以△OBC为等边三角形.所以OB=BC.因为A,B,D三点在⊙O上,所以OA=OB=DO.所以OB=BC=CD=DO.所以四边形OBCD是菱形.
上述8种证法均较有代表性.若再深入探究,尚有其他证法.学生基于直观想象,从“形结构”和“数形结合”两方面均可完成求证,解题维度多样.形象地说,试题为学生准备了不同的入口,进入后,均可发现相应的求证途径.在多维的证法中有的简捷有的曲折,这需要学生对解法进行优选.在有限的时间内,学生要从众多的解法中实现优选,这拔高了对直观想象能力的要求,而这恰是命题的亮点.
批改中的典型错误对数学教学的启示
1.注重概念教学,强化“四基”“四能”的教学
本题作为一道中档题,预设难度不高,但在批改中发现了较多的错误.错误突出表现在,学生对数学概念掌握不牢,直观想象能力较差.如在第(1)问中,相当多的学生不能在图形中直观发现∠AEO和∠CED是一组对顶角,从而构成不了两三角形全等的条件,解题思路被迫中断.也有学生根据“AE=CE,OE=DE”直接得到AC⊥OD的结论,虽然AC与OD的确是垂直的位置关系,但根据上述两条件直接得到该结论,理由不足,由此可见学生不能很好地掌握基本图形的性质.还有学生由“AE=CE,OE=DE”得到四边形OCDA为平行四边形,从而得到∠OAE=4DCE,加上AE=CE,OE=DE后,堂而皇之地用“SSA”去证△AOE≌△CDE.因此,在教学中教师要注重生成概念的过程教学,使学生体会蕴含其中的思想方法和数学素养,教学中还要发展学生的几何直观能力,如让学生经常思考图形中的问题,如图形的条件、图形彼此间的关系、需要确定的结论等,尝试用图形来描述、理解并解决问题题可见,教学中教师有必要提高学生掌握“四基”“四能”的水平.
2.在概念教学中厚植数学核心素养
李邦河院士认为:“数学根本上是玩概念的,不是玩技巧.技巧不足道也![4]”由此可见数学概念教学的核心地位.但在现实教学中,只重视概念运用,淡化概念的形成过程,甚至用解题技巧代替概念学习的现象大量存在,重解题、轻概念的现象使数学概念教学长期处于扁平化、浅层次、低效率的层面,学生的解题思路狭窄,解题过程笨拙,难以达到高效、简捷、灵动的层面,本题即是代表.在批改第(2)问时笔者发现,学生缺少直观想象,不能形成明确的证明思路,指向性混乱,错误率较高.数学概念蕴含着深厚的历史文化背景、丰富的思想方法,严谨的抽象、推理和建模过程,让学生经历概念的“形成”过程,从而积累数学活动经验,体悟思想方法,锤炼思维品质,提高解题能力,提升数学核心素养,这是改变“重解题、轻概念”的康庄大道.
3.基于直观想象,培养学生的优选能力
试题中两小问的证法均不唯一,在多维度的证法中,简单与复杂并存,直观与推理同在.本题除了考查学生对图形基本性质的掌握情况和基本的逻辑推理外,最具价值的是考查了学生建立在直观想象上的优选能力.从较多的解法中,众多的图形中,能够迅速地确定解题的优选思路,对学生的挑战极高.学生要达到这样的高度,需要教师在教学中要有目标地让学生积累经验,要注重培养学生的直观识图能力和说题能力,要深挖一题多解的教学内涵,要对多维度的解题思路进行评价、优选,帮助学生建立基于直观想象的优选眼光,培养学生的极速优选能力,这也是本题应产生的教学价值.
参考文献:
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018.
[2]孔凡哲,史宁中.中国学生发展数学核心素养概论[M].上海:华东师范大学出版社,2021.
[3]李霞.初中平面几何的推理教学之研究[J].初中数学教与学,2021(01):13-15.
[4]李邦河.数的概念的发展[J].数学通报,2009,48(08):1-3.

