关注有效问题 打造深度课堂——以一节中考几何复习课为例

景昱波

(观成武林中学，浙江 杭州 310000)

课堂是教师与学生通过知识演示、问题互动、同伴交流等方式传播知识的重要阵地．为了引发学生的深度学习，发展数学核心素养，教师在课堂中设计的问题发挥着重要的引领作用．学生在问题的解决过程中逐步感悟数学的魅力，体会数学思想方法，积累可迁移的解题经验，从而达到深度学习的目的，让学生学会学习数学．笔者在浙江省杭州市初中数学中考复习会议中开设了几何专题复习课——对一个几何图形的探究，现将本节课的教学设计予以呈现，并提出相应的教学思考．

1 基本情况分析

1.1 适用范围

本节课是中考一轮复习完后的几何专题复习课，学生已对初中所学的基本几何图形的基础知识进行了复习强化．本节课通过对一个以菱形为背景的几何图形进行探究，意在引导学生从整体与局部的关系、从静态到动态的视角展开研究．这样的研究方法与之前基本几何图形的学习保持了结构的整体性和逻辑的一贯性，对研究其他复杂的几何图形同样具有示范性．

1.2 教学内容分析

几何是研究图形的形状、大小与位置关系的学科，对于几何图形的研究可以从定性分析到定量计算，其中定性分析可以先从整体图形的形状关系入手，再研究局部的要素，如边、角之间的数量关系和位置关系．而在定量计算时，通过边的计算，引导学生归纳出初中阶段求长度的几种常用方法，从而培养学生的几何直观、逻辑推理能力．将图形从静态到动态可以进一步去研究在变化过程中不变的关系，并利用函数思想研究变量间的关系．基于以上分析，确定本节课的教学重点：从整体到局部、从静态到动态的视角对几何图形展开研究．

1.3 学情分析

学生已经经历初中阶段各种几何图形的学习，对研究几何图形的基本思路与方法有一定的了解，为本节课的学习提供了经验.九年级的学生已经具备较复杂的代数运算能力和几何论证能力，为本节课提供了能力基础．学生在研究复杂图形时，可能存在的问题有:在定性分析时可能会从局部的图形要素入手，而不知可以从整体出发再到局部展开研究;在边角的定量计算时，学生会有自己擅长的方法，但是可能缺少系统的方法总结;当图形在动态过程中产生变量，学生可能对于分析变量之间的关系存在问题．基于以上分析，确定本节课的教学难点：逐步形成对复杂几何图形从整体到局部、从定性到定量、从静态到动态的有序的研究思路．

1.4 教学目标

1)通过活动设计，能从整体到局部对几何图形进行定性分析．达成该目标的标志是：经历自主探究图形的过程，理解几何是研究图形的形状、大小与位置关系，定性分析时能形成从整体到局部展开研究的思路．

2)能运用相似三角形、勾股定理、面积法、锐角三角函数等方法，解决求几何长度的定量问题．达成该目标的标志是：通过给图形中的要素(边、角)赋值，能利用相似三角形、勾股定理、面积法、锐角三角函数等方法进行定量计算，并对方法进行归纳．

3)通过图形从静态到动态的变化，能进一步探究图形中要素的变化规律．达成该目标的标志是：图形在动态变化过程中，能利用函数的思想去研究变量的变化规律．

2 教学过程设计

2.1 开放问题，激发学生的探索兴趣

图1

活动1如图1，在菱形ABCD中，∠ABC=60°，E是BC上一点，∠EAF=60°，联结EF交AC于点P.

问题1请根据所给条件仔细观察图形，你能得到哪些结论？将其写在黑板上．

学生发现的结论：△AEC≌△AFD，△AEB≌△AFC，△AEB∽△EPC，△AEC∽△FPC∽△APE．△AEF是等边三角形，有许多相等的边和角，例如BE=CF，∠EAC=∠FAD等，以及点A，E，C，F共圆．

教学说明该题原本是一个几何综合题，这里将其改编为一个开放的问题，让学生独立思考，从而得出尽可能多的定性分析的结论，进而起到自主复习、主动学习的作用，同时实现对这一基本图形的深度挖掘．当然教师仍需要通过问题串的设置，让学生有意识地从整体到局部进行定性分析，理清研究脉络．

追问1有同学发现了△AEC≌△AFD，△AEB≌△AFC，你能进行简单的证明吗？

追问2图形之间除了全等关系以外，还有什么关系？

追问3你发现哪些三角形间的相似关系？请简单证明.

追问4以上结论是从哪个角度获得的？还可以从哪些方面获得结论呢？

生1：以上是从图形之间的形状关系获得的结论，还可以从单一图形的形状判定获得结论，例如△AEF是等边三角形．

生2：还可以从图形的局部要素，即边与角的数量关系与位置关系出发获得结论，例如BE=CF，∠EAC=∠FAD，以及点A，E，C，F共圆．

追问5根据刚才两位同学的补充，请问如何才能更全面地对复杂图形进行定性分析呢？

教学说明学生写在黑板上的结论可能是无序的、无关系的，此时需要教师通过巧妙地设问，引导学生理清结论间的关系，并自主总结出在定性分析几何静态图形时，可以按照整体图形的形状、图形间的形状关系以及图形要素之间的数量和位置关系进行分类．

2.2 问题驱动，引发学生回顾基本方法

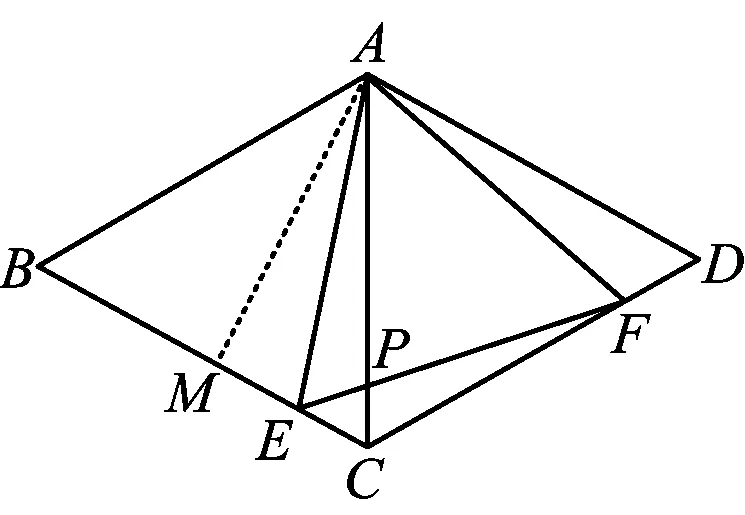
图2

活动2如图2，在活动1的图形背景下，若点E是线段BC的四等分点，BE>EC，且CE=1．

1)求点E到AB的距离；

2)求AE，CP的长；

问题1如何解决第1)和第2)小题？请分享一下你的思路．

教学说明通过第1)和第2)小题，引发学生思考求线段长度的3种一般方法：面积法、相似法、勾股法．当然不同的学生会有自己擅长的方法，但是通过学生间的交流，让学生初步体会求长度问题的一般方法，激活学生的思路，为后续解决第3)小题做铺垫．

思路1聚焦相似三角形，解决问题.

1)大部分学生会结合上一小题所得的线段AE，CP的长以及题干条件，利用△AEP∽△FPC，分别求得EP，PF的长，从而得解．

图3 图4

思路2聚焦勾股定理，解决问题.

思路3聚焦面积法，解决问题.

图5

教学说明教师通过问题设置，驱动学生解决问题，并在经验分享中比较不同思路之间的异同，从而归纳线段求长度的常用方法有:相似三角形、勾股定理、面积法、锐角三角函数等．从活动1对复杂图形有序的定性分析，再到活动2对其边的定量计算，目的在于提高学生“从挖掘图形中的关系到运用关系解决问题”的能力，真正做到在课堂上发展学生的几何直观、推理与运算的能力，注重数学核心素养的培养．

2.3 问题进阶，促进学生深度学习

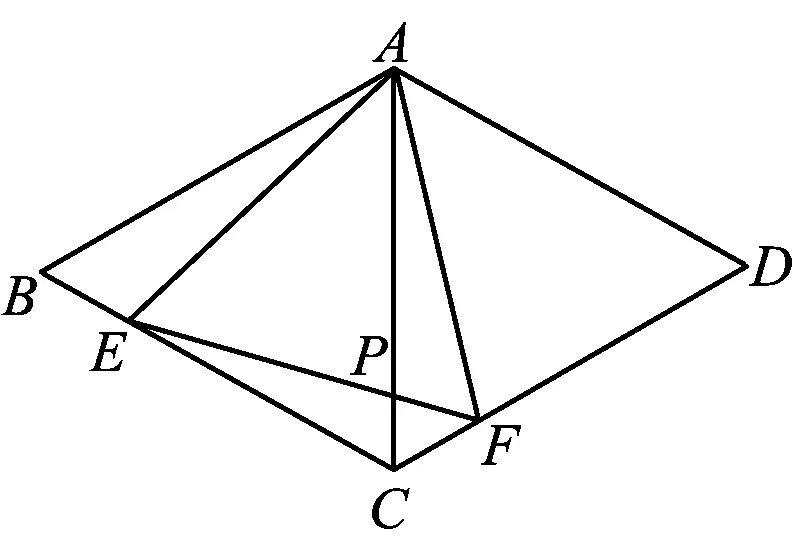
图6

活动3如图6，在菱形ABCD中，∠ABC=60°，点E是BC上一动点，∠EAF=60°，联结EF交AC于点P.

问题1在活动1的静态图形下得到的结论在动态过程中仍然成立吗？

追问1请大家和之前的结论一一对照，并进行证明.

师生活动教师利用几何画板反复让点E进行运动，学生观察，并给出几何论证：静态下的结论在动态过程中仍然成立.学生在论证过程中，理解在动态过程中需在“变”中寻“不变”.

教学说明当静态图形探究完后，自然而然联想到“若是动态图形，则情况会怎样”，于是问题的难度得到提升.同时在“变”中寻找“不变”的关系，这样的探究思路符合几何图形研究的一般思路，为后续研究其他动态几何图形奠定基础，有利于学生进行深度探究.

问题2在图6的背景下，图形动态变化过程中有哪些变化的量，它们是如何变化的？

生1：在点E的运动过程中，发现变化的量有线段的长度，例如AE，AP，还有△AEF和△ECF的面积.

追问1若BC=4，则当点E运动到何处时，△AEF的面积最小？

追问2若BC=4，则在点E运动过程中，线段AP如何变化？

追问3你用什么方法表示变化规律？

图7

师生活动学生通过几何画板可以发现:在点E的变化过程中，AP先变小后变大．而在表示变化规律时存在问题，教师通过引导让学生发现在动态过程中△AEC∽△APE始终成立，可得AE2=AP·AC.如图7，作AM⊥BC交BC于点M.设BE=x，则

EM=|2-x|，

从而

AE2=EM2+AM2=x2-4x+16.

再结合AE2=AP·AC，可得

从而可利用关于线段BE的函数来表示线段AP的长度变化.

追问4我们还可以研究哪些变化的量？它们如何变化，可求什么，运用什么方法来求？

教学说明图形在动态变化过程中，存在变化的量，学生能够通过几何直观发现图形是如何变化的.可是，对于学生来说“怎样变化，如何刻画”存在一定的困难.教师通过引导，结合之前探索的“变”中“不变”的结论，帮助学生利用函数的思想去研究变量的变化规律，从而达成教学目标;最后再次利用开放的设问，激起学生的研究兴趣，将学生的思维层层递进，促进学科的深度学习．

2.4 提问小结，帮助学生梳理思路

1)本节课我们是如何研究静态几何图形的？

2)定量计算的常用方法有哪些？

3)本节课我们是如何研究动态几何图形的？

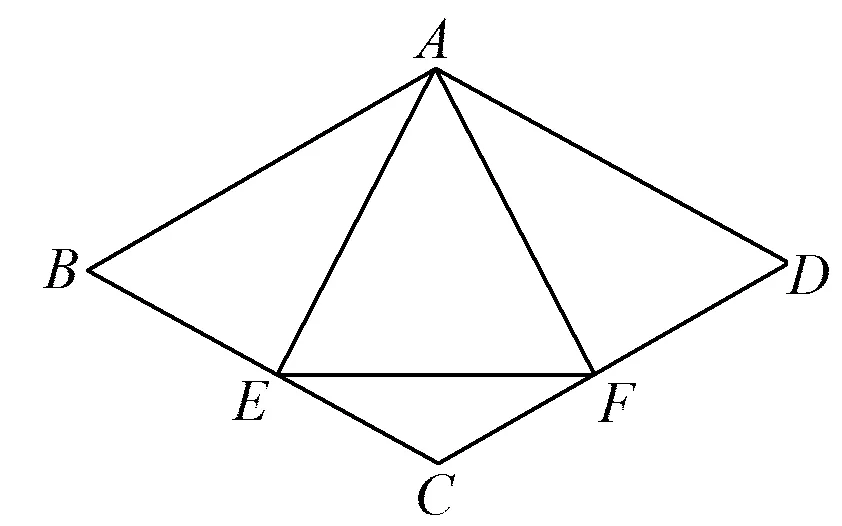
图8

课后练习1如图8，在菱形ABCD中，点E，F分别为边BC，CD上的点，且CE=CF，联结AE，EF．记△CEF的面积为m，△AEF的面积为n．

1)证明：△ABE≌△ADF；

2)若AE⊥BC，CF∶AE=2∶3，求sinD；

3)设BE∶EC=a，m=3-a，试说明当a取何值时，n的值最大，并求出n的最大值．

教学说明通过提问小结和适时的板书帮助学生形成复杂几何图形的研究思路．教师在教学过程中不仅要教给学生知识，而且要引导学生学会整理，并进行归纳与总结，从而促进深度学习的发生．最后学生通过有效的练习，将方法进行迁移与应用，从而做到真正的理解与运用．

3 教学思考

所谓深度学习，就是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程．深度学习应具备的主要特征有：1)知识的联系与结构；2)问题的本质与变式；3)方法的迁移与应用．

3.1 有效问题促进学生形成知识的联系与结构

本节课是中考几何复习课，学生已经对于所学的几何图形的基础知识有所复习．在活动1中，利用开放性的问题，引导学生从不同的角度对几何图形进行定性分析，并说出所发现的结论．随后教师巧妙地设置问题串，帮助学生理清结论背后的基础知识和它们之间的联系．在活动2中，利用问题驱动，让学生聚焦定量计算中的求线段长度问题，在学生间的相互交流后，归纳解决问题的基本方法．通过两个活动中的有效提问，学生明确了知识间的逻辑关系，整理了问题解决的方法，并逐步形成了从整体到局部、从定性分析到定量计算的研究思路．

3.2 有效问题帮助学生理解问题的本质与变式

整节课由一个主旋律、两个乐章组成，这里的主旋律是指帮助学生理清复杂几何图形的研究思路，两个乐章指的是复杂图形在静态和动态情况下的联系与不同．初中阶段正是学生逻辑思维和抽象能力形成、完善、提升的重要阶段[1]．在学习过程中培养学生发现问题的本质与联系，建立深度的探究意识，形成解决问题的思路是教师应该关注的．在活动3中，设计进阶性的问题，先让学生明确图形在动态变化过程中，需要关注“变”中的“不变”，思考活动1中所发现的结论是否仍然成立，再让学生关注变量，思考用函数的方法表示变量间的关系．最终帮助学生理解“无论问题如何变化，其本质都是挖掘图形中的关系”并运用关系去解决问题.

3.3 有效问题引导学生进行方法的迁移与应用

本节课在教学过程中，教师通过有效的提问帮助学生充分挖掘问题的本质，在变化和应用中促使学生深入思考[2]，形成解决问题的研究思路，即在研究复杂几何图形中从整体到局部、从定性到定量、从静态到动态的研究思路．课后通过有效的练习，进行方法的迁移与应用．当然除了数学知识和方法外更需要注重数学思想的培养，《义务教育课程标准(2011年版)》指出：数学思想蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括．而数学活动的积累是提高学生数学素养的标志．

本节课一直关注发展学生的几何直观、推理能力与运算能力．因此有深度的课堂就需要教师在教学中有意识地进行数学思想方法的渗透，从而使学生在数学学习中有效地提升核心素养．