基于培养创造心智的几何例题“穿越”教学设计——以圆的基本性质单元为例

陈巧薇

(建兰中学，浙江 杭州 310001)

1 培养创造心智的重要性和必要性

所谓心智是指人们对已知事物的沉淀和储存，通过生物反应而实现动因的一种能力总和.它涵盖了“哲学”对已知事物的积累和储存，结合了“生物学”的大脑信息处理，即“生物反应”，运用了为实现某种欲需(动因)而从事的“心理”活动，从而达到为实现动因结果而必须产生的智能力和“潜能”力.

在《21世纪学习的愿景》一书中，哈佛大学教授加德纳提出未来社会我们要具备的5种心智——学科心智、整合心智、创造心智、尊重心智和伦理心智.这5种心智并非未来专属，然而，有针对性地和整体地培养这些心智在当今时代显得尤为迫切.几乎每一代人都要经历不同的时代，在这个日新月异的新时代，具有良好创造心智的人往往可以跳出保守的思考，开拓出新的天地，成为时代的弄潮儿.不管在工作场所还是在实验室里，在政治舞台或是戏剧舞台上，每个人都面临着超越传统智慧或习惯性做法的压力，单纯的创新比有效的创新要容易得多[1].

创造心智不仅要具备创造力，更要综合人格与性情，在拥有知识和技艺后，竭尽全力地抓住机会，进入未知的领域去探索，即使失败也能够微笑和振作，即使成功也能燃起新的动力去再次突破.加德纳曾说：“我更乐于看到一门课程和一种教学方法改革指向于培养人的创造心智，发现并探索创造性的观念.”毫无疑问，未来社会需要更多的“大咖”创造者.

2 几何教学是培养创造心智的良好载体

初中数学中的几何教学是培养创造心智的良好载体和突出机会.基于比格斯教授提出的SOLO(StructureoftheObservedLearningOutcome，可观察的学习结果的结构)评价理论框架，即对学生某一具体问题反应的分析，根据学生解决问题时所达到的思维水平由低到高可划分为5个等级：前结构水平、单点结构水平、多点结构水平、关联结构水平和拓展抽象结构水平[2].其中关联结构和拓展抽象都和创造心智息息相关.几何学习和代数学习最大的不同在于创新，代数重在记忆和模仿，几何重在理解和创新.几何的直观性、建构性、整合性、灵活性等特点，决定了几何学习的思维难度和高度，不可能用死记硬背和照本宣科找到所有题目的几何证明方法和思路.几何题目千变万化，同时还有一题多解、同类拓展、一题多变，每一个细小的语句或者图形的变化都会导致题目的与众不同和推陈出新，因此几何教学是培养创造心智的良好载体.

义务教育教科书《数学》九年级上册第三单元圆的基本性质教材分析：这个单元是几何学习的一部分，与前面的三角形和四边形略有不同，从直线走向曲线，从多边形到圆，这是第一层直观认知的创新突破.这个单元的题目更是灵活多变，思维要求较高，从圆的概念形成、圆本身的性质、圆中的量之间的关系和圆中有关量的计算等方面加强对圆的认识．圆是一种特殊的几何图形，它对于培养学生的数学能力、形成数学的思想方法具有重要的价值．由于圆既是中心对称图形又是轴对称图形，学生可以通过多种方式来认识它[3]，这样有助于培养学生的数学能力.同时圆的有关性质的探索是通过多种方法进行的，每一次新的定理和性质都带来创新和突破，这是第二层能力的创新突破.这个单元的内容在培养创造心智方面具有非常典型的价值.

下面以圆的基本性质单元为例，尝试一个例题穿越不同的新课，每次的“似曾相识”和每次的“与众不同”形成冲击，每次的“同题异思”和每次的“创新挑战”产生火花，推陈出新，引导学生承上启下，理解新知，学以致用，融会贯通.这个通用的例题是笔者在设计本单元教学中精心挑选的一个“托”，出现在在不同新课的例题或者习题中，虽然是一样的题目，但是通过不断的探究式学习和创新式思考，每次都能找到新的解题方法.在教学设计中，教师给予学生充分的思考空间，激发学生足够的创新热情，培养学生“胜不骄、败不馁”的性情，体会到知识越多，方法越多，能力越强，解题越有晋级感.在分析问题—解决问题—重新认知—探究创新中提升学生的解题能力，培养创造心智，发展数学核心素养.

3 例题穿越教学设计说明

3.1 经典例题初相识

经典例题初相识在本单元的第3.2节“图形的旋转”，本节课的重点是图形的旋转的概念和性质.此例题是经过笔者思考挑选的具有“特别价值”的可以穿越的经典例题，在新课作为其中一个例题出现.

图1

例1如图1，在⊙O中，AB=CD，AB，CD的延长线相交于点P.

1)联结OA,OB,OC,OD和AC，是否存在旋转全等的三角形？请找一找.

2)求证：PA=PC.

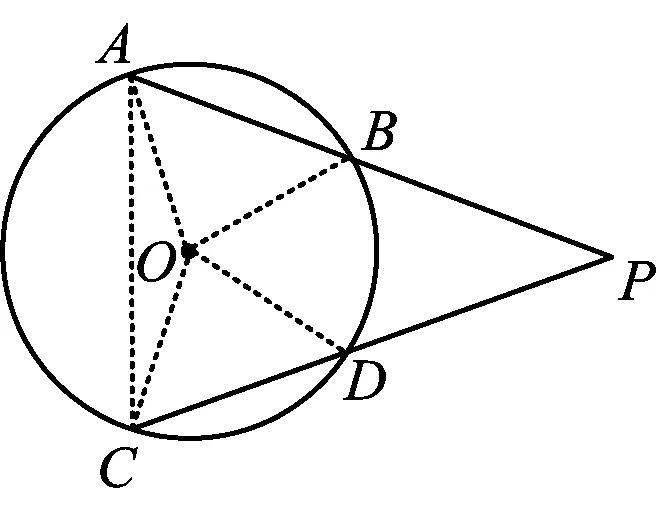
图2

评注这节课学习了图形的旋转，圆绕着圆心旋转任意角度都能和本身重合，于是称圆为旋转对称图形.当联结OA,OB,OC,OD时，我们发现了旋转后可以重合的部分，于是引导学生联系以前学习的三角形知识,通过三角形的全等证明PA=PC.

学生比较自然地给出了不同的证明思路，笔者整理了部分典型思路如下：

思路1如图2，先用圆的旋转对称性说明△OAB≌△OCD，从而

∠OAB=∠OCD.

又因为OA=OC，得

∠OAC=∠OCA,

进而

∠PAC=∠PCA,

所以

PA=PC.

思路2如图3，联结BD.根据△OBD是等腰三角形和△OAB≌△OCD，得∠OBA=∠ODC,从而

∠PBD=∠PDB，

于是

PB=PD，

进而

AB+PB=CD+PD，

故

PA=PC.

图3 图4

思路3如图4，作OE⊥AB于点E，作OF⊥CD于点F.利用等腰三角形三线合一性质可知，点E,F平分弦AB，CD，从而

AE=BE=CF=DF.

根据△OEB≌△OFD(HL)或△OAB≌△OCD(SSS)，得

OE=OF.

再利用△OEP≌△OFP(HL)，得

PE=PF，

故

PA=PC.

分析学生们对这个例题有很多想法，以上3种思路基本都是基于三角形全等的已有知识，仅仅用了圆的半径相等这个简单的条件，通过线段和差、等角对等边的性质得到线段相等的结论.此题出现在这一节，最重要的是为后面的教学做铺垫，学生们认为自己已经很成功了，有这么多解法，并且已经有较为简单的证明思路了.在这种已经学得很好的前提下，后面再出现这个题目，让学生们打破常规思路，从而达到更好的对比和刺激效果.

3.2 常规例题再创造

本单元第三节课“垂径定理”和第四节课“圆心角定理”主要学习了：在同圆或者等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各对量都相等.教师在课堂中又给出了例1.

学生们马上反应：“这个题目我们上节课做过了！”教师接着问：“今天结合新学的圆心角定理，大家有什么新的思路吗？不妨来挑战一下！”这一问果然激发了学生们的热情，他们开始动脑筋思考了.经过探究合作，教师收集了部分学生的解答如下：

思路4如图5，联结OP，作OE⊥AB于点E，作OF⊥CD于点F.根据垂径定理可知

AE=BE, CF=DF.

根据圆心角定理得弦心距OE=OF,利用

△OEP≌△OFP(HL)，

可得

PE=PF，

从而

PA=PC.

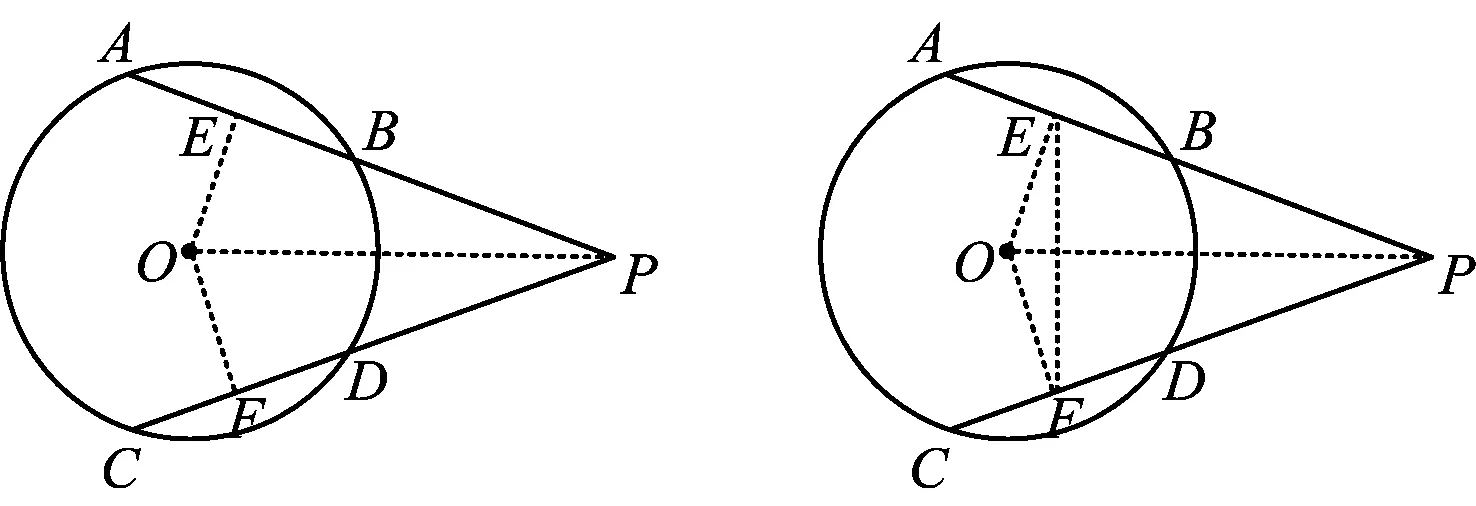
图5 图6

思路5如图6，作OE⊥AB于点E，作OF⊥CD于点F，联结EF.根据圆心角定理直接可得

OE=OF，

从而

∠OEF=∠OFE.

因为OE⊥AB，OF⊥CD,所以

∠PEF=∠PFE, PE=PF.

再由垂径定理及条件AB=CD,得

AE=BE=DF=CF,

故

PA=PC.

分析学生们感受到同样的例题有了更多新的解法，这两种思路与之前的相比确实简化了很多.之前只能通过全等去证明线段相等，现在有了更直接的方法：因为AB，CD是弦，根据弦相等可以直接得到弦心距相等，弦相等也可以直接转化为圆心角相等，所以有了线线转化和线角转化的新思路.实际上，学生们的解题思路还有更多，但是教师刻意去突出垂径定理和圆心角定理的优势，让学生们体会到“新式武器”带来的便利和好处.当然在课堂中依然有墨守成规的学生，在不同的思路对比中，教师鼓励学生打破固有的思维，哪怕已经有成果，我们依然寻找不同的机会去突破，创新永不止步，这正是创造心智的必然要求.

3.3 熟悉例题再突破

这个熟悉的例题第3次出现在第3.4节“圆周角定理”中，这节课的主要内容是圆周角等于它所对的弧的度数的一半.教师问：“大家来看看这个习题，今天我们新学了圆周角定理，想一想这个题目会有新的解题思路吗？同学们都踊跃尝试一下吧，比一比谁的方法更新、更优！”

于是激动人心的“再创造”“再突破”开始了，不论前面失败或者成功的学生，都有“激情”“热情”再去动脑筋，他们已经接受了暗示，在寻找真理的路上.大家思考的积极性很高，于是又有学生给出了新的解法，并且激动的心情和骄傲的神情溢于言表.具体思路如下：

∠BAD=∠BCD.

∠CAD=∠ACB，

因此

∠PAC=∠PCA，

故

PA=PC.

图7 图8

∠PAC=∠PCA，

故

PA=PC.

到这里，教师可以给出思路1～思路7的过程对比，让学生们总结发言.

学生们发出“年年岁岁花相似，岁岁年年人不同”的惊叹——最后利用圆周角定理，思路变得如此简单明了！在几次解题中教师也在反思：学生们会有什么经验总结和收获呢？除了从知识层面、技能层面进行总结，对于同样的一个“例题的穿越”，每次都带来不同的反响和震撼，所学皆有用，所思皆有益，以后我们在分析问题的时候，就要联系多个知识点，综合应用所学的知识，训练自己的创造性思维，寻找到最优解法.

在这里，显性的收获是在总结解题经验，提升解题能力.更多隐形的收获融合在整个3次例题穿越教学过程中，每一节课情感上的冲击和收获都不一样.在“思考探究—再创造—再突破—总结反思”的过程中，师生一次次打破原有的解法，一步步创新思考，不论成功或者失败，每一次都有全新的视角，拥有创造的动力和热情，探究出更多、更新、更优的方法，整个经历激发了学生的创新热情，培养了学生的创造心智，体验了探究创新的神奇.

4 基于培养创造心智的教学设计收获和反思

创新是引领世界发展的重要动力，今天的中国比以往任何时候都更加需要创新驱动、创新发展.就初中数学教学而言，我们要抓住一切可以利用的机会激发和培养学生的创造心智，这种创造心智来源于对新知的好奇、对应用的思考、对困难的挑战以及对真理的坚持.

笔者以几何教学为载体，用藕断丝连的“穿越”例题的设计，让学生感受创新的平易近人——每节课都可以带着创新思考和学习，又让学生感受创新的高深莫测——每一次创新都不是终点，“新”无止境.这样的设计或许有些刻意，但是确实起到了培养创造心智的作用.笔者认为不仅是圆的基本性质这个单元，其他几何课程也可以有类似的效果.在平行四边形到特殊四边形的教学中，在三角形到三角函数的教学中，我们都可以去研究如何设计出“穿越”例题，把创新在平常教学中潜移默化.

认知理论认为：理解是新信息与原有知识经验相互作用的过程，要使新、旧知识能够发生作用、建立联系.创新是打破学生已有的认知结构、认知发展水平和已有的知识经验，推陈出新，是从无到有的过程.创新能力是技术和各种实践活动中不断提供具有经济价值、社会价值、生态价值的新思想、新理论、新方法、新发明的能力.创造心智除了创新能力，还包括人格和性情，以延伸为特性.

在几何教学中，我们基于培养创造心智而设计教学，在分析问题—解决问题—重新认知—探究创新中培养创造心智，力求让学生经历探究式学习和创新式思考后达到知识、能力、素养的共同提升.一个例题的穿越带来的是关于创新的无止境的追求，带来的是对于创新的无条件的热爱.爱默生曾说：“品格比智力更为重要.”因此，在教学中培养创造心智非常有必要.