地面堆载对埋地管道的影响分析
淦 邦,朱 磊,史振龙,董志博
(1.国家管网集团东部原油储运有限公司,江苏 徐州 221008;2.中国科学院、水利部成都山地灾害与环境研究所,四川 成都 610041; 3.中国科学院大学,北京 100392)
1 概述
油气管道作为一种线性工程,不免要穿越某些地质状况复杂的地区,软土作为一种含水率大、孔隙度大、压缩性高的特殊土[1],受到荷载或扰动时会对管道产生复杂的摩擦作用,导致管道的破坏[2-5]。其中,地面堆载对软土地区埋地管道的不良影响是最常见且最容易被忽略的因素,由于以上原因导致的地基不均匀沉降,会使管道产生弯曲变形甚至破裂,并可能引发油气泄露。如在2017年12月3日,仪长线原油管道大武支线发生焊口撕裂,原油泄漏并进入距离管线断口处70 m的废弃灌溉渠内,直接威胁灌溉渠下游的武汉市严东湖。
针对地面堆载作用下埋地管道的受力特性,常见的研究方法有现场监测、物理模型试验和数值模拟[6-9],由于现场监测和物理模型实验容易受到现场条件的限制,无法针对埋地管道变形的主控因素进行参数敏感性分析,所以亟需通过数值模拟等方式评价外部荷载对管道应力应变的影响方式。如李长俊等[10]利用ANSYS有限元软件模拟了地表的堆载对埋地管道的影响。帅健等[11]建立了地基-管道三维有限元模型,分析了不同强度地基状态时地表荷载对管道的影响方式。陈剑健[12]通过结合Boussinesq法和弹性地基梁理论建立了地表荷载作用下的管道力学模型,并采用有限差分法对其求解,计算出地表堆载对埋地管道产生的变形和应力。
本文主要应用ABAQUS有限元软件,建立了地表堆载作用下管-土相互作用模型,研究了荷载大小、堆载体-管道水平距离、管道埋深以及荷载面积对埋地管道变形及稳定性的影响规律,本文研究结果可为油气埋地管道的设计与施工提供一定的参考。
2 有限元模型建立
2.1 管道本构模型
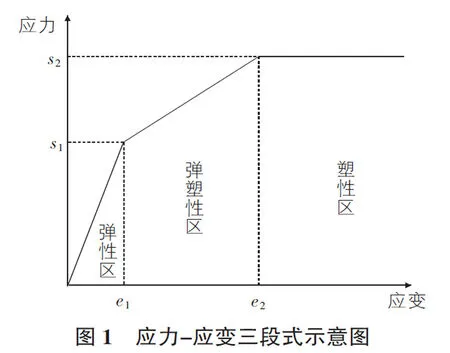
由于管道的非线性本构关系,且本文涉及对管道极限荷载状态的分析,所以本文参照文献[10]和文献[13],选取经典的三段式应力应变关系曲线(如图1所示)作为数值模拟中管道的本构模型。图1中s1,s2分别为弹塑性变形和塑性变形的起始应力;e1,e2分别为弹塑性变形和塑性变形的起始应变。
2.2 土体本构模型
本文中土体本构模型选用摩尔-库仑模型,结合勘察资料设置黏聚力及摩擦角等参数来拟合现场土体工程性质,黏聚力可以体现屈服面的软、硬化状态,适用于对外部荷载作用敏感的土体,是一种很好体现岩土体拉压变形不相等特点的本构模型,已被广泛应用[14]。
2.3 管土相互作用
管道和管周土体之间存在复杂的相互作用,由于非线性有限元模型的发展[15-19],本文选用表面-表面接触类型作为模型中管-土接触模型。由于管道刚度远大于土体,设置管道外表面为主表面,与管道外表面相接触的土体表面为从表面。定义管土接触的切向和法向行为,法向行为选取“硬接触”,符合管土接触后可分离的实际情况,切向行为设置摩擦系数为0.5的“罚”函数来定义。
2.4 物理模型及参数
根据输油钢管管材技术要求执行标准GB/T 9711—2011石油天然气工业管道输送系统用钢管[20],并对研究区管道参数进行调研,本文数值模型管道采用L320钢材料为原型,管道外径D=762 mm,壁厚=8.7 mm,具体材料参数如表1所示。管周土体为黏土,土体模型尺寸为40 m×40 m×8 m,土体尺寸设置为管径的50余倍,根据圣维南原理满足边界条件对管道应力不构成影响,土体底面采用完全固定约束,上表面为自由表面,4个侧面则固定住其对应法线方向的运动。按土体表面通过施加一定范围的均布荷载代替地面堆载。

表1 管道材料参数
3 结果分析
3.1 荷载大小对埋地管道的影响规律
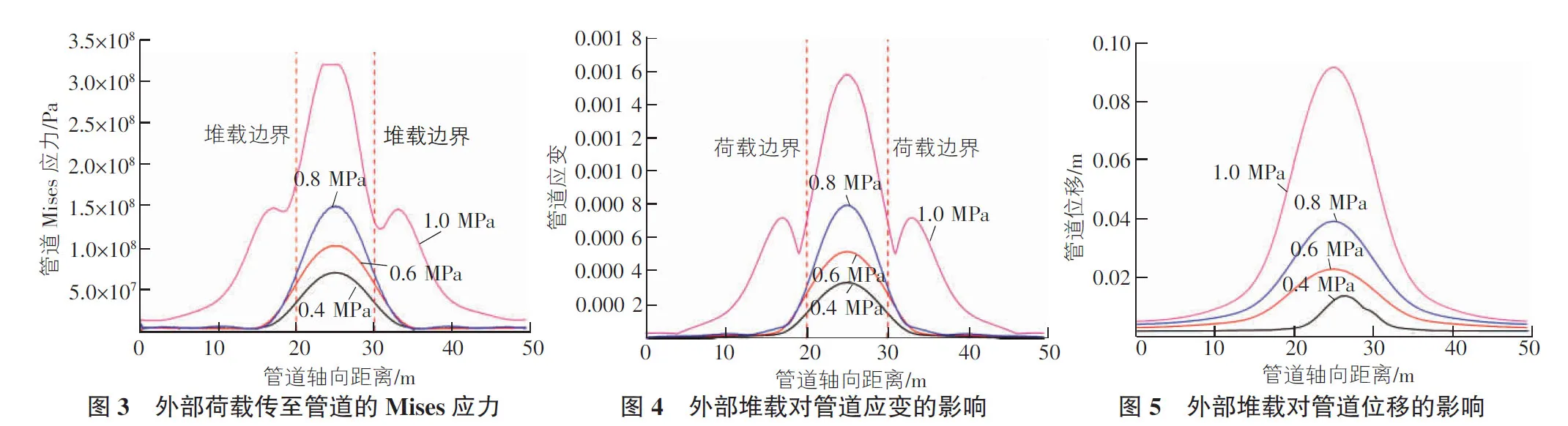
图2为地表堆载与管道位置关系俯视图,其中A,B两点之间的范围即定义为地表荷载在管道上的投影范围,A1,B1两点间距定义为堆载体长度。图3为外部荷载不同程度时,管道轴向上的Mises应力分布,图4为受外部荷载影响的管道轴向应变分布。图3和图4中显示,管道应力值随着外部荷载重量的增加迅速增大;而且位于地表荷载在管道上的投影范围以内(20 m<管道轴向距离<30 m)的Mises应力值和应变值的增幅要远大于荷载投影面以外的增幅;同时可以看出,当地表外部荷载的重量达到一定程度时(图3中为1.0 MPa),地表荷载在管道上的投影范围外附近(管道轴向距离等于25 m及35 m)所对应的管道Mises应力和应变会稍大于边界外的一段管道的应力和应变,总体呈现一个“笔架”型的变化趋势(在图4中的应变分布图中,这个趋势尤为明显),所以在现场监测中,要重点关注地表荷载在管道上的投影中心所对应的管道点位,也要重视荷载投影边界所对应的管道位置的力学状态和变形特征。
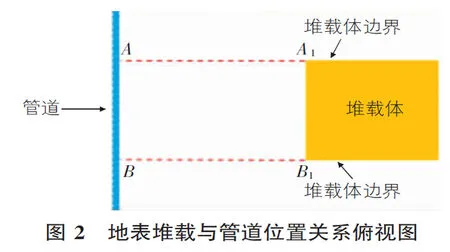
图5为外部荷载不同程度时,管道轴向上的位移分布。由图5可知,地表堆载重量越小,堆载体对埋地管道的影响越小,当堆载重量小于一定数值时(本文为0.4 MPa),仅有堆载体投影内所对应的管道受外部堆载影响而产生位移。反之,随着堆载重量增加,管道位移迅速增大;而且位于荷载在管道上的投影范围以内(20 m<管道轴向距离<30 m)的位移值的增幅要远大于投影范围以外的增幅。
3.2 埋置深度对管道的影响规律
控制地表荷载为0.6 MPa,堆载体-管道间距为5 m,堆载体长度为10 m。图6~图8分别表示管道不同埋深下,管道的水平向应力峰值、水平向应变峰值及水平向位移峰值。由图6~图8可知,随着管道埋深的增加,地面荷载对埋地管道的影响越来越小,本文中管道埋深达到5 m时,荷载对管道已无明显作用。这是由于随着地面堆载引起的附加应力随着土体深度的增加逐渐减小,也可理解为随管道埋深增加,管道远离地表荷载有效作用区域,从而限制了管道的运动,对管道抵抗变形有利。但这部分只考虑了地表荷载对管道水平方向上应力、应变和位移状态的影响,并未考虑管道上覆土压力、孔隙水压力等的影响,而这些关键变量随管道埋深都可能会对管道应力和变形产生显著的不利影响,因此并不能简单的提出,管道埋深越大,管道就越安全的结论。

3.3 堆载距离对管道的影响规律
图9为堆载体偏离管道中轴线不同程度时,管道轴向的Mises应力分布图,图10为管道轴向距离应变分布图。图中显示,应力值和应变值随堆载体-管道距离的增加而迅速减小,堆载体对埋地管道的影响越小,而且位于载荷投影面以内(20 m<管道轴向距离<30 m)的Mises 应力值和应变值的降幅要远大于荷载投影面以外的降幅。同时由图9可以看出,地表荷载导致的管道Mises 应力在间距为2倍荷载长度(A1,B1)时几乎为0,故在本文中,地表荷载影响长度可以取为荷载长度的2倍,堆载体-管道间距超出这一数值,可认为地表荷载对埋地管道无显著影响。

图11为堆载体偏离管道中轴线不同程度时,管道轴向位移分布图,从图11可知,当荷载距离管线轴线位置增加时,管道位移降幅明显。当间距为2倍荷载长度,即20 m时,管道的最大位移几乎为0,这是因为地面荷载下方产生一个沉陷区,该沉陷区存在竖向和水平方向的位移,荷载位置移动相当于该沉陷区在移动,随荷载与管道距离增大,管道远离沉陷区,管道竖向和水平向位移均减小。

4 结论
应用ABAQUS有限元软件建立了地表堆载工况下的埋地管道的土体-管道相互作用三维模型,通过数值模拟,研究了堆载重量、管道埋深、堆载体-管道间距对管道力学状态和变形特征的影响规律。1)管道应力值和变形程度会随着外部荷载重量的增加而迅速增大,而且位于载荷投影面以内的Mises应力值、应变值和位移的增幅要远大于荷载投影面以外的增幅。2)管道水平方向应力、应变、位移的峰值随管道埋深增大而减小,但此时未考虑上覆土体、孔隙水压力等对管道的作用,不能直接认为管道埋深越深,管道越安全。3)管道应力、应变、位移随堆载体与管道之间距离的增大而减小。当堆载体与管道间距离超过20 m时,地表堆载几乎不对管道产生影响。本文针对地表堆载工况下的埋地管道的土体-管道相互作用的研究可以为埋地管道的建设与防护提供一定参考。

