分析错因加强防范
■蒙春凤
指数函数与对数函数是重要的基本初等函数,指数函数与对数函数的图像与性质容易混淆,因此,解题时稍有不慎就会出错。下面就此类问题,举例分析错因,加强防范意识。
例1化简:(1-a)[(a-1)-2·

防范措施:化简指数式时,应讨论其中字母的取值范围,通常根据指数幂的指数来讨论,也可以化为根式,利用偶次方根的被开方数为非负数,奇次方根的被开方数是任意实数求出其中字母的取值范围。如(am)n=amn,当a>0时,(am)n=amn成立;当a<0,m为偶数时,
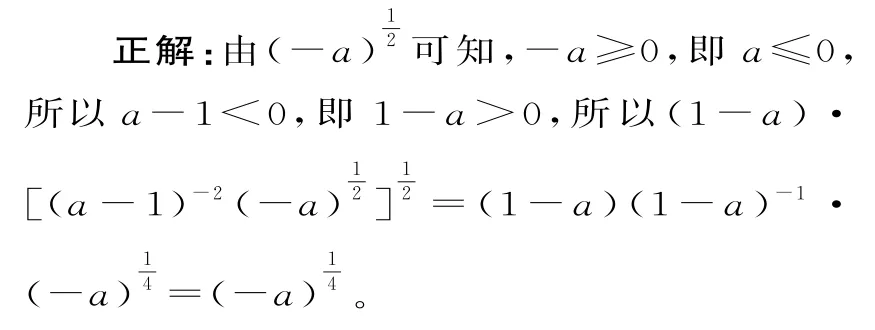
二、忽视对指数函数的底数a 的讨论
例2求函数且a≠1)的定义域。
错解:要使此函数有意义,需满足ax-1≥0,即ax≥1,解得x≥0。
错因分析:解不等式ax≥1时,结合指数函数的单调性,需对底数a进行分类讨论。上述错解默认了底数a>1。
防范措施:对涉及含参数的不等式问题,要注意对参数进行分类讨论。
正解:要使此函数有意义,需满足ax-1≥0,即ax≥1。
当a>1时,可得x≥0;当0 综上可得,当a>1时,函数的定义域为[0,+∞);当0 错因分析:换元时,要结合指数函数的性质,确定t的取值范围。 防范措施:在进行换元变换时,一定要等价换元,也就是换元后一定要确定新变量的取值范围,否则,换元后的变量与原变量不等价,从而产生错误结果。 例4解方程log3(x2-10)=log3(3x)。 错解:原方程可化为x2-10=3x,即x2-3x-10=0,解得x=-2 或x=5。故原方程的解为x=-2或x=5。 错因分析:上述错解忽视了对数的真数为正的情况。 防范措施:解关于对数方程或对数不等式时,一定要等价转化,注意对对数的真数大于0的检验。 正解:原方程可化为 由x2-10=3x得x=-2或x=5。 由3x>0得x>0,由x2-10>0得x>或x<-。 经检验知x=5符合题意,所以原方程的解为x=5。 例5已知lgx+lgy=2lg(x-2y),则的值的集合为( )。 A.{2} B.{0,2} C.{4} D.{0,4} 错因分析:上述解法忽视了对数的真数大于0的限制。 防范措施:熟练掌握对数的运算法则是解题的关键。解答与对数有关的问题时,必须注意对数式本身的限制条件。 正解:由已知可得lg(xy)=lg(x-2y)2,所以xy=(x-2y)2,整理得x2-5xy+4y2=0,即(x-y)(x-4y)=0,所以x=y或x=4y。 由x>0,y>0,x-2y>0,可得x>2y>0,所以x=y(不合题意,舍去),所以x=4y,即 例6求函数的定义域和值域。 错解:由题意可得-lg(1-x)≥0,即lg(1-x)≤0,也即lg(1-x)≤lg1,所以1-x≤1,解得x≥0,所以此函数的定义域为[0,+∞)。 因为-lg(1-x)≥0,所以≥0,所以此函数的值域为[0,+∞)。 错因分析:上述解法对对数的取值理解不清晰。实际上,当底数a>1时,若logax≤0,则0 防范措施:解答本题时,要注意题中的隐含条件。 正解:由题意知-lg(1-x)≥0,可得lg(1-x)≤0,即lg(1-x)≤lg1,所 以解得0≤x<1,所以此函数的定义域为[0,1)。 因为-lg(1-x)≥0,所以0,所以y≥0,所以此函数的值域为[0,+∞)。三、换元时忽视中间变量的取值范围


四、解对数方程时,忽视真数的取值范围
五、对数运算,忽视真数大于0
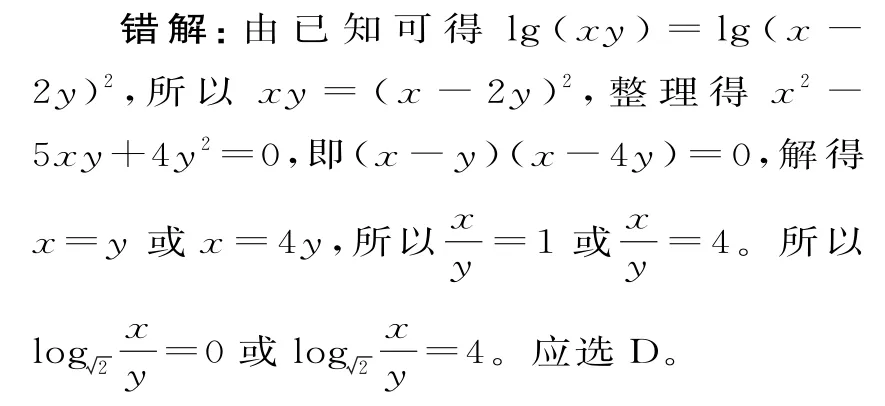
六、求函数的定义域时,忽视对数函数的真数的取值范围



