指数函数与对数函数常见典型考题赏析

■赵 昆 张文伟

指数函数与对数函数是基本的初等函数,指数函数与对数函数是高考的常考点。这部分的主要知识点有:指数、对数的化简与求值,指数函数与对数函数的图像与性质的应用,利用指数函数和对数函数解决某些简单的实际问题,函数的零点问题,函数模型的应用问题等。

题型1:有条件的根式的化简

有条件根式的化简问题,是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简。有条件根式的化简经常用到配方法。当根指数为偶数时,利用公式化简,要考虑被开方数或被开方的表达式的正负。

例1已知,求下列各式的值。

(1)a+a-1。 (2)a2+a-2。

题型2:指数式与对数式的互化

将指数式化为对数式,只需要将幂作为真数,指数当成对数值,底数不变,即可得到对数式;将对数式化为指数式,只需将真数作为幂,对数作为指数,底数不变,即可得到指数式。

例2将下列指数式与对数式互化。

跟踪训练2:下列指数式与对数式互化不正确的一组是( )。

A.e0=1与ln1=0

C.log39=2与=3

D.log77=1与71=7

题型3:指数函数的定义域与值域问题

对于y=af(x)这类函数,①定义域是指使f(x)有意义的x取值范围。②值域应分以下两步求解:由定义域求出u=f(x)的值域;利用指数函数y=au的单调性或利用图像求出此函数的值域。对于y=(ax)2+b·ax+c这类函数,①定义域是R。②值域可分以下两步求解:设t=ax,求出t的范围;由二次函数y=t2+bt+c,结合配方法求出值域。

例3若函数的值域为[0,+∞),则实数a的取值范围是____。

解:设g(x)=4x+a·2x+1。若函数的值域为[0,+∞),则等价于[0,+ ∞)是g(x)值域的子集。g(x)=4x+a·2x+1=(2x)2+a·2x+1,设t=2x,则t>0,所以g(x)等价于y=h(t)=t2+at+1。

因为h(0)=1>0,所以当对称轴t=,即a≥0 时,不满足条件。当t=,即a<0时,由判别式Δ=a2-4≥0,即可得a≤-2。故所求实数a的取值范围是(-∞,-2]。

A.(0,1) B.(0,1]

C.(-1,1) D.[-1,1]

题型4:指数函数的图像与性质问题

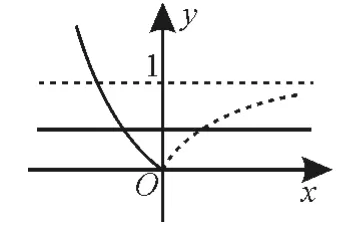
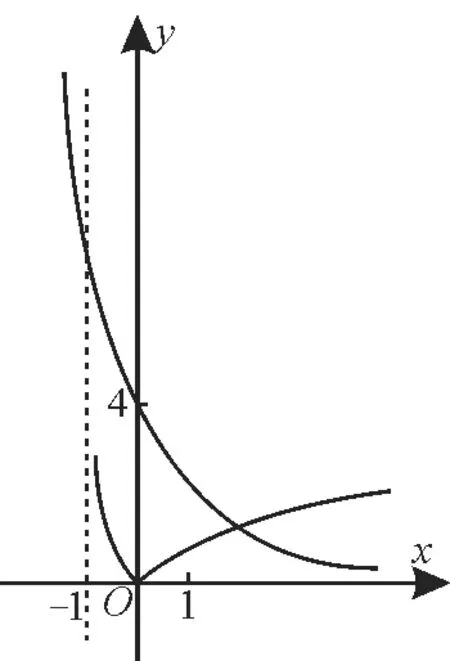
对于函数y=af(x)+b(其中b是常数),令f(x)=0,解得x0,y=b+1,则此函数过定点(x0,1+b)。函数y=a|x|(a>0,且a≠1)是偶函数,图像关于y轴对称,当x>0时的图像即为函数y=ax的图像。根据指数函数图像判断底数大小的方法:作直线y=1与所给图像相交,交点的纵坐标即为各个底数,在第一象限内,自下向上,图像对应的指数函数的底数逐渐变大,即遵循“图高指大”的原则。如指数函数y=ax1,y=ax2,y=ax3,y=的 图 像 如 图1 所示,其中0

图1

指数函数性质记忆口诀:若底数大于1,图像从下往上增;底数在0到1之间,图像从上往下减;无论函数增和减,图像都过(0,1)点。

例4若直线y=2a与函数y=|ax-1|(a>0,a≠1)的图像有两个公共点,则a的取值范围是_____。

解:由01,可分别画出函数y=|ax-1|的图像,如图2,图3所示。

图2

图3

题型5:对数函数的单调性问题

函数单调性的判断方法:一般地,增函数与增函数的和为增函数,增函数与减函数的差为增函数。复合函数的单调性遵循“同增异减”的法则。对于与对数函数有关的复合函数,要注意真数恒大于零的情况。

例5(1)函数f(x)=log3(-x2+2x+3)的单调减区间是( )。

A.(-3,1) B.(1,3]C.(-1,1) D.(1,3)

(2)已知f(x)=loga(3-2ax)在[1,2]上是增函数,则实数a的取值范围是( )。

解:(1)由题意得-x2+2x+3>0,即(x+1)(x-3)<0,解得x∈(-1,3)。

函数f(x)=log3(-x2+2x+3)的减区间,即为y=-x2+2x+3 的减区间。y=-x2+2x+3的对称轴为x=1,结合二次函数的单调性,可得f(x)=log3(-x2+4x+5)的减区间为(1,3)。应选D。

(2)令y=logau,a>0 且a≠1,u=3-2ax。因为f(x)在[1,2]上是增函数,u=3-2ax在[1,2]上是减函数,所以y=logau是减函数,且u>0 恒成立,即解得。应选C。

跟踪训练5:已知函数f(x)=lg(x2-4x-5)在(a,+∞)上单调递增,则a的取值范围是( )。

A.(2,+∞) B.[2,+∞)C.(5,+∞) D.[5,+∞)

提示:由x2-4x-5>0,可得x<-1或x>5。令t=x2-4x-5。外层函数y=lgt在定义域内是增函数,要使f(x)=lg(x2-4x-5)在(a,+∞)上单调递增,只需内层函数t=x2-4x-5在(a,+∞)上单调递增且恒大于0,所以(a,+∞)⊆(5,+∞),即a≥5。应选D。

题型6:对数式的比较大小问题

若底数为同一常数,则可由对数函数的单调性直接进行比较。若底数为同一字母,则根据对数函数单调性,对底数进行分类讨论。若底数不同,真数相同,则可以先用换底公式化为同底后再进行比较,也可以利用顺时针方向底数增大的规律画出函数的图像,再进行比较。若底数与真数都不同,则可借助1,0等中间量进行比较。

例6比较下列各组数中两个值的大小。

(1)log23.4,log28.5。

(2)log0.31.8,log0.32.7。

(3)loga5.1,loga5.9(a>0,且a≠1)。

解:(1)对数函数f(x)=log2x在(0,+∞)上为增函数,因为3.4<8.5,所以log23.4

(2)对数函数f(x)=log0.3x在(0,+∞)上为减函数,因为1.8<2.7,所以log0.31.8>log0.32.7。

(3)当0loga5.9。当a>1时,对数函数f(x)=logax在(0,+∞)上为增函数,因为5.1<5.9,所以loga5.1

跟踪训练6:已知a=log20.3,b=0.31.3,c=21.3,则a,b,c的大小关系是( )。

A.a

C.b

提示:因为a=log20.32,所以a

题型7:对数函数的图像与性质的应用

当函数y=m+logaf(x)(a>0,且a≠1)的图像过定点时,只需令f(x)=1,求出x,即得定点为(x,m)。根据对数函数图像判断底数大小的方法:作直线y=1与所给图像相交,交点的横坐标即为各个底数,在第一象限内,自左向右,图像对应的对数函数的底数逐渐变大,即可比较底数的大小。因为对数函数的单调性与底数有关,所以要注意是否需要分类讨论。

例7函数y=loga(-x)(a>0且a≠1)与函数y=ax(a>0且a≠1)在同一直角坐标系内的图像可能是( )。

解:当01 时,y=ax和y=logax均为增函数,而y=loga(-x)的图像和y=logax的图像关于y轴对称,A 正确。应选A。

跟踪训练7:已知函数f(x)=,a为常数。

(1)若a=-2,求证f(x)为奇函数,并指出f(x)的单调区间。

提示:(1)当a=-2 时,函数f(x)=,所以函数f(x)的定义域为

题型8:求函数的零点问题

求函数的零点的两种常用方法:代数法,根据零点的定义,解方程f(x)=0,它的实数解就是函数y=f(x)的零点;几何法,若方程f(x)=0 无法求解,可以根据函数y=f(x)的图像与性质求出零点。

例8若函数f(x)=ax+b(a≠0)的零点是2,则函数g(x)=ax2+bx的零点是( )。

A.2 B.2和0

C.0 D.-2和0

解:由题意知f(2)=0,所以b=-2a,所以g(x)=ax2+bx=ax(x-2)。令g(x)=0,可得g(x)的零点为0和2。应选B。

跟踪训练8:已知函数f(x)=则函数f(x)的零点为( )。

提示:当x≤1时,令f(x)=2x-1=0,解得x=0。当x>1 时,令f(x)=1+log2x=0,解得,因为x>1,所以此时方程无解。综上所述,函数f(x)的零点只有0。应选D。

题型9:判断函数的零点所在的区间

判断函数的零点所在区间的三个步骤:将区间端点值代入解析式求出函数的值;把所得的函数值相乘,并进行符号判断;若符号为正且函数在该区间内是单调函数,则在该区间内无零点,若符号为负且函数连续,则在该区间内至少有一个零点。

例9函数f(x)=lnx+x3-9的零点所在的区间为( )。

A.(0,1) B.(1,2)

C.(2,3) D.(3,4)

解:由题意得x>0,且f(x)在其定义域内为增函数。因为f(2)=ln2-1<0,f(3)=ln3+18>0,所以此函数的零点在区间(2,3)内。应选C。

跟踪训练9:函数f(x)=2x+x-4的零点所在的区间是( )。

A.(-1,0) B.(2,3)

C.(0,1) D.(1,2)

题型10:判断函数零点的个数问题

判断函数零点的个数的三种方法:方程法,若方程f(x)=0的解可求或能判断解的个数,可通过方程的解来判断函数是否存在零点或判断零点的个数;图像法,由f(x)=g(x)-h(x)=0,得g(x)=h(x),在同一坐标系内画出y1=g(x)和y2=h(x)的图像,根据两个图像交点的个数来判断函数零点的个数;定理法,函数y=f(x)的图像在区间[a,b]上是一条连续不断的曲线,由f(a)·f(b)<0即可判断函数y=f(x)在区间(a,b)内至少有一个零点,若函数y=f(x)在区间(a,b)上是单调函数,则函数f(x)在区间(a,b)内只有一个零点。

例10(1)函数的零点个数为( )。

A.0 B.1 C.2 D.3

(2)方程lnx+x=0的实数解的个数为( )。

A.1 B.2 C.3 D.0

解:(1)令y=0,则=0,即-x2+x+5=0。因为Δ=1+20>0,所以该方程有两个不同的根,且均满足函数的定义域。故该函数有两个零点。应选C。

(2)方程lnx+x=0 的实数解的个数,即为方程lnx=-x的实数解的个数,也就是函数y=lnx与函数y=-x图像的交点的个数。在同一直角坐标系中,画出函数y=lnx与函数y=-x的图像,如图4所示。

图4

由图像可知,y=lnx与y=-x的图像只有一个交点,所以方程lnx+x=0的实数解的个数为1。应选A。

跟踪训练10:函数f(x)=2x·|ln(x+1)|-4的零点个数为_____。

提示:令f(x)=2x·|ln(x+1)|-4=0,则。在同一直角坐标系中,画出函数y=|ln(x+1)|与y=22-x的大致图像,如图5所示。

图5

由图像可知,当x→-1时,y=|ln(x+1)|→+∞,则函数y=|ln(x+1)|与y=22-x的图像必有两个交点,所以方程有两个不同的实根,所以函数f(x)=2x·|ln(x+1)|-4的零点个数为2。

题型11:二分法求方程的近似解

将方程转化为相应的函数,根据二分法求方程近似解的步骤循环进行,直到方程近似解所在的区间符合精确度要求。对于区间内的任一点,都可以作为零点的近似解,一般取端点作为零点的近似解。

例11在用“二分法”求函数f(x)零点的近似值时,第1 次所取的区间是[-2,4],则第3次所取的区间可能是( )。

A.[1,4] B.[-2,1]

解:因为第1 次所取的区间是[-2,4],所以第2次所取的区间可能为[-2,1],[1,4],所以第3 次所取的区间可能为。应选D。

跟踪训练11:下列函数图像与x轴均有公共点,其中能用二分法求零点的是( )。

提示:能用二分法求零点的函数必须在给定区间[a,b]上连续不断,且f(a)·f(b)<0,A,B中不存在f(x)<0,D 中函数不连续。应选C。

题型12:常见的函数模型及增长特点

线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变。指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,即增长速度急剧,形象地称为“指数爆炸”。对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓。幂函数y=xn(n>0)的增长速度介于指数增长和对数增长之间。提醒:函数值的大小不等同于增长速度的大小,数值大不一定增长速度大,增长速度体现在函数值的变化趋势上。

例12一种药在病人血液中的量保持1500mg以上才有效,而低于500mg病人就有危险。 现给某病人注射了这种药2500mg,如果药在血液中以每小时20%的比例衰减,为了充分发挥药物的利用价值,那么从现在起经过( )向病人的血液补充这种药,才能保持疗效。(参考数据:lg2=0.301,lg3=0.4771,答案采取四舍五入精确到0.1h)

A.2.3h B.3.5h C.5.6h D.8.8h

解:设从现在起经过xh 向病人的血液补充这种药,才能保持疗效。由2500×0.8x=1500,可得0.8x=0.6,所以lg0.8x=lg0.6,即xlg0.8=lg0.6,所以≈2.3(h)。应选A。

跟踪训练12:某品牌牛奶的保质期y(单位:天)与储存温度x(单位:℃)满足函数关系y=akx+b(a>0,且a≠1)。该品牌牛奶在0℃的保质期为270 天,在8 ℃的保质期为180 天,则该品牌牛奶在24 ℃的保质期是( )。

A.60天 B.70天 C.80天 D.90天