声圆阵模态域最小方差无畸变高分辨方位估计

宋海岩,唐 弢,迟凤阳

(黑龙江工程学院 电气与信息工程学院,哈尔滨 150050)

阵列信号处理技术又称为空-时处理技术,广泛应用于雷达、通信、声呐、射电天文、医学诊断、地震遥感等众多领域[1]。该技术通过获取空间中传播的信号,根据实际应用需求,对信号进行时域与空域分析和处理,最终获得所需要的有效信息。空间目标方位估计问题是阵列信号处理领域的研究热点,与之相关的技术在近几十年来得到迅猛发展[2]。最早的空间目标方位估计技术称为波束形成(Conventional Beamforming,CBF),它是一种空间滤波技术,然而其性能却依赖阵列的物理孔径,角度分辨力受“瑞利限”的制约。如何突破“瑞利限”成为一个热门的研究方向,并促进了空间谱估计技术的兴起与发展,由此产生了高分辨空间谱估计方法[3]。例如,最大熵谱法(Maximum Entropy Method,MEM)采用参数模型化的方法对空间谱进行分析,突破了“瑞利限”的限制[4]。最小方差信号无畸变响应法(Minimum Variance Distortionless Response,MVDR)在保持来波方向、信号能量不变的条件下,使波束内其他方向的能量最小化,该方法可同时具有较高的空间分辨力和较强的噪声干扰抑制能力[5]。随着阵列信号处理的广泛应用,许多满足不同特定需求的阵列结构应运而生,其空间分布形状也多种多样[6]。其中,以均匀线列阵(Uniform Linear Array,ULA)和均匀圆阵(uniform circular array,UCA)较为典型。然而,相比于均匀线列阵,均匀圆阵具有2个明显优势:1)可提供360°全空间方位角估计的同时,还可对俯仰角进行估计;2)在进行方位角扫描时,其波束形状可保持不变。这些优势促使圆阵方位估计方法迅猛发展[7]。现阶段,圆阵方位估计方法分为两种:一种是基于阵元域的经典信号处理方法;另一种是基于相位模态(phase modes)的模态域方位估计方法,文中主要研究讨论第二种方法[8]。近年来,广大学者对圆阵模态域方位估计方法进行了广泛研究。Mathews等[9]提出对窄带信号方位角进行估计的求根子空间类算法,该方法实质上是在波束空间中进行估计,且依赖于相位模态激发形式。Rafaely等[10]发表了一系列基于圆阵麦克风阵列进行室内声学分析的报道,其核心思想是利用高阶球面谐波改善算法的空间分辨能力。文献[11]提出一种基于球谐波分解的最大似然方位估计方法,该方法避免了球贝塞尔函数的分离并能适用于任意频率。在文献[12]中,研究者提出了4种时延求和波束形成器,并对其性能进行详细地仿真和讨论。王永良等[13]针对均匀圆阵模式空间变换的算法,提出了模式空间平滑算法和改进的MODE算法。然而,纵观现有圆阵模态域方位估计研究成果,大多数文献以电磁波为信号载体开展研究,却很少讨论水下声场条件下的圆阵模态域信号模型,同时,鲜有文献采用最小方差无畸变处理器进行圆阵模态域高分辨方位估计。

基于此,文中从柱坐标系下的水下声波散射理论出发,构建圆阵接收信号模型,并利用模态域变换矩阵获得模态域阵列接收数据,在此基础上,将最小方差无畸变处理器引入圆阵模态域方位估计领域,提出了一种基于水下声圆阵模态域的最小方差无畸变高分辨方位估计方法。数值仿真结果表明所提出方法的有效性,尤其在低信噪比、相干源和小快拍数条件下,该方法能够分辨距离较近的空间目标,较传统波束形成方法具有更高的空间分辨能力和更好的方位估计性能。

1 柱坐标系下的圆柱薄壳水下声波散射理论

弹性力学中的薄壳理论在实际工程中应用广泛,目前已推导出多种形式的圆柱薄壳振动方程[14]。如图1所示,令圆柱壳体中心和柱坐标系的原点重合,轴线方向和z轴重合。圆柱壳体半径为a,长度为2l,内部流体密度为ρ0,声速为c0,外部流体密度为ρ,声速为c,壳体材料密度为ρs,杨氏模量为E,泊松比为σ,壳体厚度为h,远场平面波入射方向为(φ0,θ0)。

图1 圆柱薄壳结构

圆柱壳体外部流体中的声压场可表示为

p=pinc+pscat.

(1)

式中:pinc为入射声场;pscat为散射声场。

在圆柱壳体中部表面,正横方向附近开角不大的范围内可以将入射声场pinc和刚性散射声场pscat近似为无限长刚性圆柱的解,则在柱坐标系(r,φ,z)下有[15]

(2)

(3)

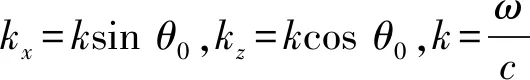
2 圆阵模态域信号模型及模态域方位估计方法

2.1 常规圆阵输出信号模型

假设空间存在一个半径为a的圆柱体,一点声源位于该圆阵远场处,其入射声波可视为平面波。根据前述对声波散射理论和现象的讨论可知,圆柱体周围空间分布的声场为入射波和散射波的叠加。为简化起见,令入射平面波在xoy平面内传播,即其传播方向与圆柱的中心轴相垂直,φ=π/2。θ0代表入射波方位角。对于刚性圆柱散射体而言,其声学阻抗远远高于周围介质阻抗,结合前述讨论的声波散射理论,则柱坐标系下的声压可表示为

P(kr,θ)=Pinc(kr,θ)+Pscat(kr,θ)=

(4)

式中:下标inc和scat分别表示入射波和散射波;k=2πf/c为波数,f为信号频率,c为声在介质中的传播速度;Jm为球贝塞尔函数;Hm为球汉克尔函数;j为纯单位虚数;(·)′为求导运算。

若圆柱体不存在,则散射波不复存在,柱坐标系下的声场将进一步表示为

(5)

值得说明的是,式(4)同样也可通过将平面波展开成傅里叶级数形式而得到。至此,已经获得了柱坐标系下的声场表示形式,接下来讨论圆阵的输出信号模型。

为简便起见,这里描述窄带信号模型。假设均匀圆阵位于xoy平面且由N个阵元组成,则圆阵接收到的声压(r=a)可表示为

(6)

为表示简便,定义bm=jmJm(ka)为声传递函数,则式(6)可重新表示为

(7)

式中:Pm=bme-jmθ0为第m阶模态或特征波束(EigenBeams,EBs)。

进一步考虑K个窄带信号,sk(t)入射至空间均匀圆阵,入射角度为θk,则第n个阵元输出信号为

(8)

假设阵列输出受加性噪声的干扰,则圆阵输出的矩阵形式可以表示为[16]

P(ka,t)=FB(ka)A(θ)S(t)+n(t).

(9)

式中:F为空间傅里叶变换矩阵;B(ka)为传递函数对角矩阵;A(θ)为模态域阵列流型矩阵;S(t)为源信号矩阵;n(t)为噪声矩阵。

2.2 圆阵模态域方位估计方法

在圆阵阵元域信号模型的基础上,进一步构造模态域变换矩阵

(10)

将模态域变换矩阵T作用于式(9),即可得到模态域阵列接收数据

X(t)=TP(ka,t)=A(θ)S(t)+N(t).

(11)

式中:X(t)为模态域输出信号;N(t)=Tn(t)为噪声场。

进一步观察式(11)可以看出,通过应用模态域变换矩阵T对阵元域信号模型进行变换,模态域合成了类似于均匀线阵的阵列流型。换句话说,得到一个“虚拟”线阵。至此,基于传统阵元域方位估计算法(如常规波束形成技术CBF、最小方差无畸变算法MVDR)可直接应用于模态域处理。

常规波束形成技术CBF是经典的时域傅里叶频谱分析技术在空域的拓展,该处理器可直接应用于模态域空间[17]

(12)

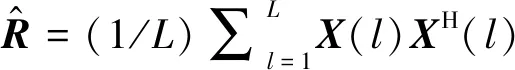
最小方差无畸变算法MVDR在保持来波方向θ不变的情况下,最大程度地抑制噪声或其他干扰方向的影响。在数学表达上可以表示为

(13)

式(13)表明,最小方差无偏估计准则即在保证所需方向信号输出为无畸变的条件下,使阵列的噪声输出功率极小化,其目的是保证来自某个确定方向θ的信号能正确接收,而其他入射方向的信号或干扰被最大程度抑制。

可以利用Lagrange常数法求解式(13),令目标函数为

(14)

对w求导,并令其为0,可以得到最优权矢量

wopt-MVDR=μR-1a(θ).

(15)

再利用wHa(θ)=1,可以得到常数μ的表达式

(16)

至此,得到在wHa(θ)=1条件下的最优权矢量

(17)

则阵列的输出功率为

(18)

该处理器可视为空间带通滤波器,其相应的算法称为模态域最小方差无畸变处理器(Eigen Beam Minimum Variance Distortionless Response Beamformer,Eigen-MVDR),空间谱估计曲线可表示为

(19)

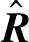
(20)

(21)

(22)

式中:上标f表示前向平滑;上标b表示后向平滑;上标fb表示双向空间平滑;Jm为m×m维反对角线是1的置换矩阵。

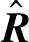
3 计算机数值仿真分析

3.1 单源方位估计

考虑一个半径为a=1.5 m的均匀圆阵,阵元个数为20个。单目标窄带信源位于圆阵远场处,并从90°方向入射。信源频率为1.0 kHz,采样快拍数为64,信噪比为10 dB。在此条件下的方位估计结果如图2所示。

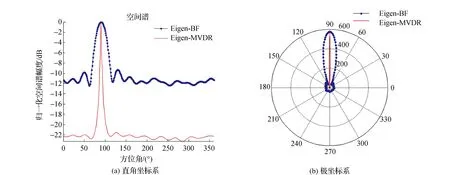
图2 空间单源目标方位估计结果

图2(a)和(b)分别表示直角坐标系和极坐标系下的单源目标空间谱估计结果。从图中可以看出,由于阵列物理孔径的限制,特征波束形成(Eigen-BF)技术的分辨能力受“瑞利限”制约,其主瓣较宽,旁瓣较高。相比之下,特征波束最小方差无畸变响应技术(Eigen-MVDR)利用了高分辨类算法处理器MVDR,因此,能突破“瑞利限”限制,较Eigen-BF具有更窄的主瓣和更低的旁瓣。以上仿真结果表明在单信源目标条件下,Eigen-MVDR算法较传统Eigen-BF算法具有更优的方位估计性能,如更低的旁瓣和更高的谱峰。

3.2 双相干源方位估计

为了进一步表明文中方法的优势,保持仿真条件基本不变,考虑两个相干信源入射情况。入射角度分别为80°和110°,信噪比为20 dB。尤其值得注意的是,在相干源条件下,信源之间的强相关性将导致阵列接收数据协方差矩阵R秩亏缺。对于最小方差无畸变响应处理器MVDR而言,需要先采用解相干算法对协方差矩阵R进行处理,然后才能对相干源进行有效估计。仿真结果如图3所示。

图3 空间相干源目标方位估计结果

图3(a)和(b)分别表示直角坐标系和极坐标系下的双相干源目标(80°和110°)空间谱估计结果。正如所注意到的,由于“瑞利限”的限制,采用常规波束形成处理器的Eigen-BF方法根本无法区分开这两个相干信源。与此同时,可以明显看出在Eigen-MVDR算法空间谱曲线中,两个谱峰之间的凹槽很深(接近15 dB),很容易分开两个目标。这说明Eigen-BF算法的性能出现明显下降,相比之下,Eigen-MVDR算法能有效处理相干源目标,在空间谱图上具有两根尖锐的谱峰,能够很好地分辨出两个不同的空间目标位置。本仿真结果表明,在双相干源且相距很近的情况下,Eigen-MVDR算法能够获得更高的分辨能力和方位估计精度。

3.3 不同信噪比条件下的均方根误差

目前为止,已经讨论并比较了Eigen-BF算法与Eigen-MVDR算法的单源及双相干源目标空间谱曲线。接下来将从统计学角度,考察以上算法在不同信噪比条件下的性能。性能衡量指标为方位估计均方根误差(Root Mean Square Error,RMSE),定义为

(23)

在本例仿真中,均匀圆阵半径为1.5 m,阵元个数为20。空间存在两个等功率信源,分别从50°和110°方位角入射至圆阵。阵列采样快拍数为64,蒙特卡罗统计试验次数为50次,信噪比由-15 dB变化到20 dB。图4为两类算法对两个目标方位估计的均方根误差随信噪比变化曲线,其中,图4(a)表示对50°目标方位估计的均方根误差,图4(b)表示对110°目标方位估计的均方根误差。

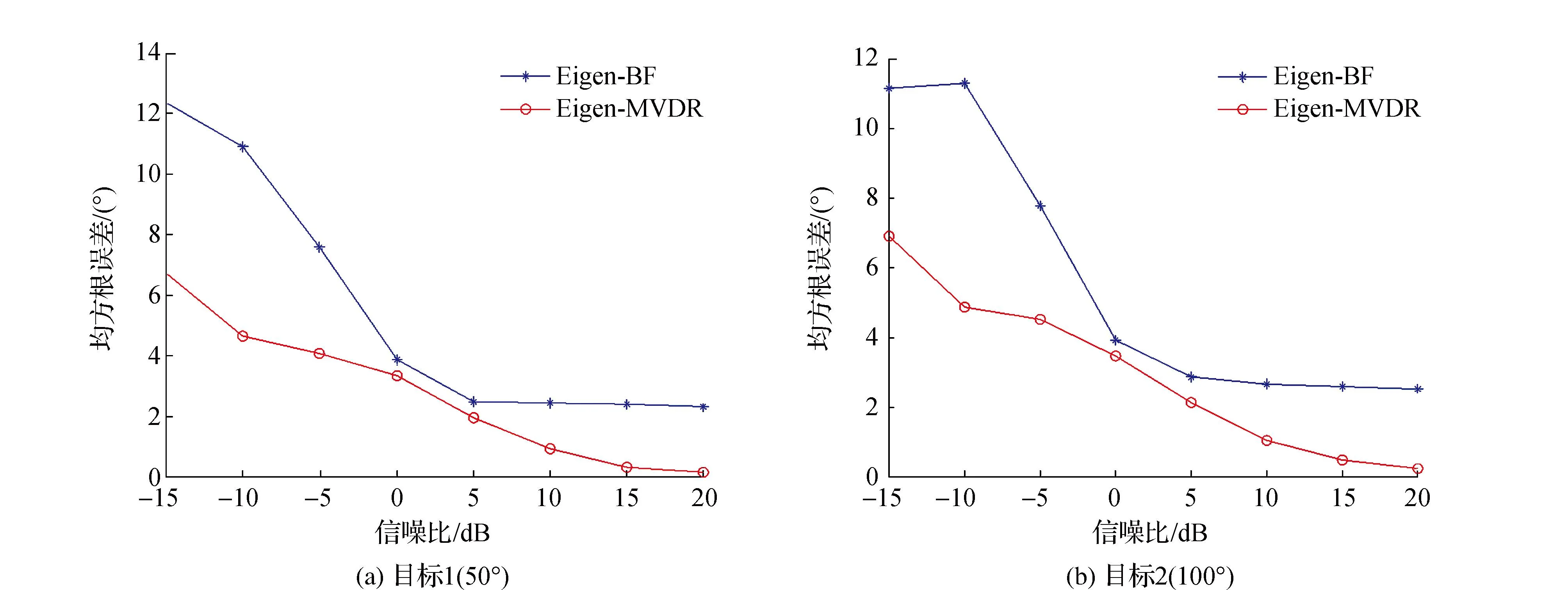
图4 不同信噪比条件下的均方根误差曲线

从图4可以明显看出,随着信噪比的增加,两种算法的均方根误差均减小。该现象与实际情况相符,算法的性能随着信噪比的增加而改善,随着信噪比的降低而恶化。然而,需要注意的是,Eigen-MVDR算法始终具有最低的均方根误差。例如,在图4(a)中,当信噪比为15 dB时,Eigen-MVDR算法的均方根误差为0.5°左右,而Eigen-BF算法却为2.5°。即使是在较低信噪比的条件下,Eigen-MVDR算法仍比Eigen-BF算法具有较低的均方根误差。这主要是由于Eigen-MVDR算法充分利用了MVDR处理器的空间高分辨能力,故能获得更高的方位估计精度。本例仿真表明文中所提出的Eigen-MVDR算法较Eigen-BF算法对噪声具有更强的稳健性和抑制能力。

4 结束语

文中提出了一种声圆阵模态域最小方差无畸变高分辨方位估计方法,该方法将圆阵接收信号转换为模态域信号,利用最小方差无畸变处理器对空间声源目标进行方位估计。得益于均匀圆阵固有的结构优势,该方法可对空间目标进行360°全方位角扫描,且保持不变的波束形状。数值仿真结果表明文中提出方法的有效性,在单目标及相干源条件下,该方法能够分辨距离较近的空间目标,较传统方法具有更高的空间分辨能力和更好的方位估计性能。