有界噪声条件下基于集员滤波的扩展目标跟踪方法

刘 盼,马天力,张 荣,李颐果

(西安工业大学电子信息工程学院,西安,710021)

目标跟踪基于最优估计原理,采用相关滤波算法对受到噪声干扰的量测信息进行处理,从而准确估计目标特征,其广泛应用于智能驾驶、视频监控、防空反导等领域[1-5]。传统目标跟踪算法主要以“点目标”假设为前提,假定一个目标最多产生一个量测。随着传感器分辨率的提高,一个目标往往可占据多个分辨单元,即可产生多个量测,该目标被称为扩展目标。不同于传统的点目标跟踪,扩展目标跟踪可以从量测集合中提取目标扩展状态信息(例如目标大小、形状和朝向等[6-7]。因其更贴近实际过程,近几年吸引了国内外学者的广泛关注。

Koch[8]于2008年首次提出基于随机矩阵模型(random matrix model,RMM)的扩展目标跟踪框架,其将目标椭圆轮廓描述为二维对称正定(symmetric and positive definite,SPD)随机矩阵,并假设目标散射源均匀散布于目标轮廓表面,并利用贝叶斯滤波对扩展目标运动状态与扩展形态进行估计。该模型仅考虑目标散射源统计特性,未考虑实际过程中存在的传感器测量误差对系统的影响。为此,Fledman等[9]提出混合加性量测噪声表示模型,其主要思想是量测的散布程度受到扩展目标形态与实际观测噪声共同作用,具体表现为两者线性组合的形式,但是其难以采用基于贝叶斯理论的滤波方法对其状态与扩展形态的后验概率密度进行求解。针对这一问题,兰剑等[10-11]提出量测噪声近似策略,通过构建形态观测矩阵对混合加性量测噪声进行近似。Liu[12]则构建乘性误差模型(multiplicative error model,MEM),该模型通过引入高斯乘性噪声项对目标散射源分布进行描述,进而利用扩展卡尔曼滤波(extended Kalman filter,EKF)和二阶扩展卡尔曼滤波(second-order EKF,SO-EKF)等[13-15]方法对扩展目标状态和形态进行估计。

在实际应用过程中,由于传感器系统受到内部热噪声和外部信号扰动影响,量测噪声可能存在非高斯性,若采用上述方法对扩展目标进行估计,极易导致目标跟踪精度降低。鉴于此,Zhang等[16]将量测噪声通过偏正态分布进行表示,利用变分贝叶斯推理计算系统后验概率密度函数。LI Yawen、Gao Lei和陈辉等提出基于Student’s t分布的量测噪声统计模型,并分别利用变分推理、鲁棒Student’s t滤波算法对扩展目标运动状态与形态进行计算[17-19]。

现有的扩展目标跟踪方法均是基于概率框架,其假设扩展目标状态以及量测服从某一特定分布,并利用贝叶斯滤波方法对其目标状态与形态进行估计。事实上,因目标加速度物理特性,外界未知环境不确定干扰,使得量测噪声具有未知但有界特性(unknown but bounded,UBB),难以运用概率框架下的相关滤波算法进行求解。因此,针对UBB噪声条件下扩展目标状态估计问题,本文提出一种基于集员滤波的扩展目标跟踪方法(extended object tracking based on set membership filter,SMF-EOT),通过UBB椭球集合对量测噪声进行表示,利用集员滤波方法对状态集合参数进行计算,在形态更新过程中,结合Graham scan策略,求得包含目标形态最大误差的最小边界矩阵,通过仿射变换和偏移超曲面对扩展目标形态进行更新,最终获得扩展目标运动状态与扩展形态。

1 问题描述

建立扩展目标状态空间模型:

(1)

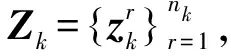
Ck=λXk⊕Uk

(2)

式中:λ为散射因子,表示目标扩展状态对量测值的影响程度,λ∈(0,1];Xk为k时刻目标形态矩阵;Uk为传感器量测误差边界;⊕表示Minkowski和。

对于上述扩展目标跟踪系统,在UBB噪声条件下如何对目标运动和扩展状态进行估计将是本文解决的核心问题。

2 基于集员滤波的扩展目标跟踪方法

2.1 集员滤波相关基础理论

对UBB噪声条件下的扩展目标进行跟踪,其主要思路是利用基于区间数学理论的集员估计方法[20],下面首先介绍集合相关定义及其运算性质。

定义1椭球集合E(x,S)表示为:

E(x,S)={y∈Rn|(y-x)TS-1(y-x)≤1}

(3)

式中:x为椭球中心;S为SPD矩阵,表示椭球形状大小。

定义2椭球集合E(x,S)的支持函数[20]表示为:

η(E(x,S))=αTx+(αTSα)1/2,α∈Rn

(4)

定理1椭球集合E(x1,S1)与E(x2,S2)支持函数的Minkowski和[20]为:

η(E(x1,S1)⊕E(x2,S2))=

η(E(x1,S1))+η(E(x2,S2))

(5)

虽然定理1给出了E(x1,S1)和E(x2,S2)支持函数的Minkowski和,但其并不是一个确定大小的椭球。因此,需找到包含Minkowski和的外定界椭球E(x,S),如图1所示。

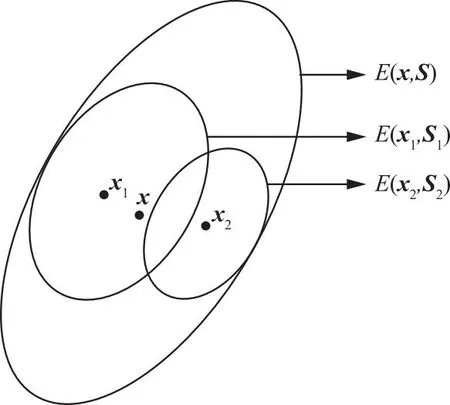
图1 外定界椭球

因此,需要根据定理2和定理3计算最优准则下的外定界椭球E(x,S)。

定理2E(x,S)为椭球集合,Σ为已知n维方阵,则:

ΣE(x,S)=E(Σx,ΣSΣT)

(6)

证明:利用支持函数可将E(x,S)表示为:

(7)

定理3已知椭球集合E(x1,S1)和E(x2,S2),包含2个椭球的Minkowski和的外定界椭球E(x,S)可表示为:

E(x,S)=E(x1,S1)⊕E(x2,S2)=

E(x1+x2,S(p))

(8)

其中:

(9)

证明考虑椭球集合E(x1,S1)和E(x2,S2),根据椭球定义:

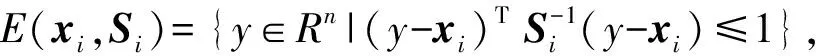
i=1,2

(10)

假定外接椭球集合为E(x,S)。

E(x,S)={y∈Rn|(y-x)TS-1(y-x)≤1}

(11)

若外接定界椭球集合E(x,S)能够包含2个椭球集合,则其支持函数必须满足下列不等式:

η(E(x,S))≥η(E(x1,S1))+η(E(x2,S2))

(12)

根据定义2,上式可变换为:

αTx+(αTSα)1/2≥αTx1+(αTS1α)1/2+

αTx2+(αTS2α)1/2

(13)

则外定界椭球中心x为:

x=x1+x2

(14)

根据式(13),将外界椭球边界S通过S1和S2的线性组合表示为:

γαTS1α+ραTS2α≥αTS1α+2(αTS1α)1/2·(αTS2α)1/2+αTS2α

(15)

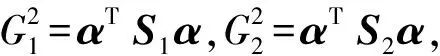
(16)

当(γ-1)(ρ-1)≥1时,式(16)成立,可行标量p需满足γ-1=p-1,ρ-1≥p,则:

γ=1+p-1,ρ=1+p

(17)

即S(p)可以表示为:

S(p)=(1+p-1)S1+(1+p)S2,p>0

(18)

通过定理3可知,2个椭球集合Minkowski和的外定界椭球是形状矩阵S关于参数p的函数。根据以下定理计算最优椭球参数p。

定理4已知椭球集合E(x1,S1)和E(x2,S2),则半轴平方和最小意义下最小迹椭球参数p。

(19)

证明最小化椭球E(x,S(p))的最小迹等价于求取如下函数的最小值。

f(p)=tr(S(p))=tr((1+p-1)S1+(1+p)S2)

(20)

将式(20)对变量p求导并令其导数等于零,即可求得函数f(p)极值时p的值:

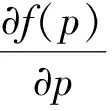
(21)

2.2 基于集员滤波的扩展目标跟踪方法

令扩展目标状态集合为χk-1⊆E(xk-1,Sk-1),xk-1为状态集合中心,Pk-1为协方差矩阵,Sk-1表示状态集合边界。由于扩展目标状态向量为集合形式,则目标运动状态估计由点估计变为状态可行集的估计。基于集员滤波的扩展目标跟踪方法对目标状态与形态的估计分别包括预测步骤和更新步骤。

2.2.1 运动状态预测

在卡尔曼滤波基础上,状态集合一步预测为:

χk,k-1=Φkχk-1⊕wk

(22)

预测协方差误差阵为:

(23)

根据定理2,结合状态空间模型,可得椭球集合Φkχk-1的支持函数如下:

(24)

由定理1可得状态集合预测的支持函数:

η(E(xk,k-1,Sk,k-1))=

(25)

要使E(xk,k-1,Sk,k-1)能够包含式中2个椭球的Minkowski和,则其支持函数必须满足:

η(E(xk,k-1,Sk,k-1))≥

(26)

根据定理2和定理3,包含状态集合χk,k-1的外定界椭球E(xk,k-1,Sk,k-1)的中心值xk,k-1及椭球大小的矩阵Sk,k-1为:

(27)

式(27)中,需计算最小迹椭球参数pSk,k-1使椭球E(xk,k-1,Sk,k-1)为包含椭球ΦkE(xk-1,Sk-1)和E(0,Qk)的Minkowski和最小外定界椭球。根据定理4可计算得到关于可行标量pSk,k-1的最小迹函数和半轴平方和最小意义下最小迹椭球参数pSk,k-1。

(28)

(29)

2.2.2 扩展形态预测

对于扩展形态Xk的预测,假设其在时间间隔内目标形态大小不发生改变[9],则k时刻扩展形态的预测Xk,k-1为k-1时刻扩展目标状态Xk-1的更新结果,即:

Xk,k-1=Xk-1

(30)

2.2.3 运动状态更新

(31)

式中:滤波增益Kk及更新误差协方差阵Pk分别为:

(32)

(33)

根据定理1和定理2,结合式(1),可得状态更新集合χk的支持函数:

(34)

类比于时间更新步骤,根据定义2和定理3可得包含状态更新集合χk的椭球E(xk,Sk)的中心值xk和椭球形状矩阵Sk。

(35)

同样,根据定理4可得关于可行标量pSk的函数表示为:

(36)

则最小迹椭球参数pSk为:

(37)

2.2.4 扩展形态更新

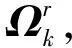
根据定理3和定理4,则第r个量测椭球集合边界为:

(38)

(39)

因量测椭球集合边界由目标扩展状态以及传感器量测误差边界信息构成。因此可将其作为目标扩展形态误差边界,即包含k时刻所有量测椭球集合的最小边界为目标扩展形态最大误差边界。由于利用椭球集合Minkowski和无法求得包含所有量测椭球的最小外接椭球,因此利用凸包计算几何中Graham scan算法计算包含k时刻所有量测椭球集合的最小边界集合A。

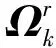
(40)

式中:dot(·)为向量点积运算符。

根据极角τi大小顺序对集合J进行排序得到Js。将Js中的每一个点ai(i≥3)与其余各点aj在二维坐标平面中求向量叉积σi,j=ai×aj。若σi,j≤0,表明ai是最小边界上的点;若σi,j>0,表明ai不是最小边界上的点。经过上述计算可得到包含所有量测椭圆的最小边界点的集合A=[a1,a2,…,am-1,am]。以a3与a2,a1为例,如图2所示。

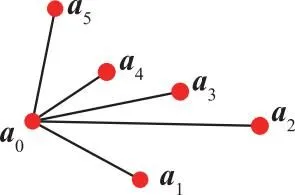
(a)

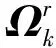
(41)

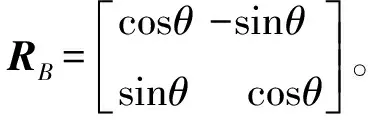
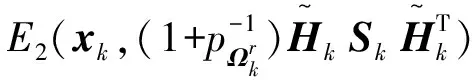
图3 E1与E2椭球Minkowski差

为求得E1⊖E2,首先利用Givens Rotation[23]对E2进行分解,计算椭圆长短半轴aE2,bE2与旋转矩阵RE2,其次利用线性变换对E1进行参数化。

(42)

式中:Di为椭球边界任意一点;ΛE1=diag(a1,b1)。

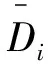
(43)

式中:ΛE2=diag(aE2/bE2,1)。将式(43)代入式(44)中,可得到经仿射变换后E1椭球边界的参数表达式:

(44)

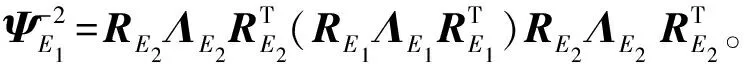
为了获得内切于E1的各圆E2的中心,利用超曲面gofs(φ)对仿射变换后E1⊖E2进行计算。

(45)

所求的偏移超曲面gofs(φ)为仿射变换后E1与E2Minkowski差的边界。如图3所示,因仿射变换后其形状大小和方向等状态发生变化,需对gofs(φ)进行仿射逆变换,使E1回到初始状态。则E1⊖E2边界的封闭解为:

(46)

根据中心xk到边界geb(φ)的距离计算E1与E2的Minkowski差所表示椭圆的长短半轴和旋转矩阵,进而可得表示E1与E2的Minkowski差椭圆的矩阵Xd,由式可知Xd可近似为集合λXk,k和Uk的Minkowski和,Xd=λXk,k⊕Uk。为了求解扩展目标形态更新矩阵Xk,k,则需要计算Xd与误差边界Uk的Minkowski差。即计算Xd⊖Uk边界的封闭解geb,Xd(φ)。

(47)

式中:RUk为Uk的旋转矩阵;gofs,Xd表示仿射变换后Xd⊖Uk的边界表达式。

(48)

式中:Dofs(φ)为经仿射变换后椭圆Xd关于角度φ的点集,通过中心xk到geb,Xd(φ)的距离对扩展目标形态更新椭圆长短轴和角度进行计算,获得更新后的扩展目标形态Xk,k。

3 仿真实验

为了验证所提基于集员滤波的扩展目标跟踪方法(extended object tracking based on set membership filter,SMF-EOT)的有效性,首先采用RMF[8]、MEM-EKF[14]、MEM-SOEKF[15]在UBB噪声条件下对扩展目标跟踪性能进行对比验证。其次,采用不同有界噪声参数对本文所提算法跟踪性能进行仿真实验分析。

3.1 机动场景仿真实验

(49)

式中:Θ为系统机动时间常数,Θ=40 s;过程噪声集合边界Qk=diag[0.52;0.52]。观测矩阵Hk=[1 0 0],量测噪声集合Ck=λXk⊕Uk,其中λ=0.25为噪声参数散射因子,量测误差边界Uk=diag{202,102}。采样间隔T=10 s。扩展目标在时间t∈[30,70]和t∈[90,130]分别做角速率为4.5 rad/s和-4.5 rad/s的转弯运动。

假设扩展目标初始状态椭球χ0=E(x0,S0),目标初始位置x0=[800,-200,9.82,-9.82,0,0]T,S0为初始椭球形状大小矩阵,初始状态协方差矩阵P0=diag[702,702,102,102,52,52],系统仿真时间为160 s。图4为4种算法一次实验的扩展目标跟踪结果,可以看出在UBB噪声条件下,本文所提SMF-EOT算法性能优于RMF、MEM-EKF、MEM-SOEKF算法。

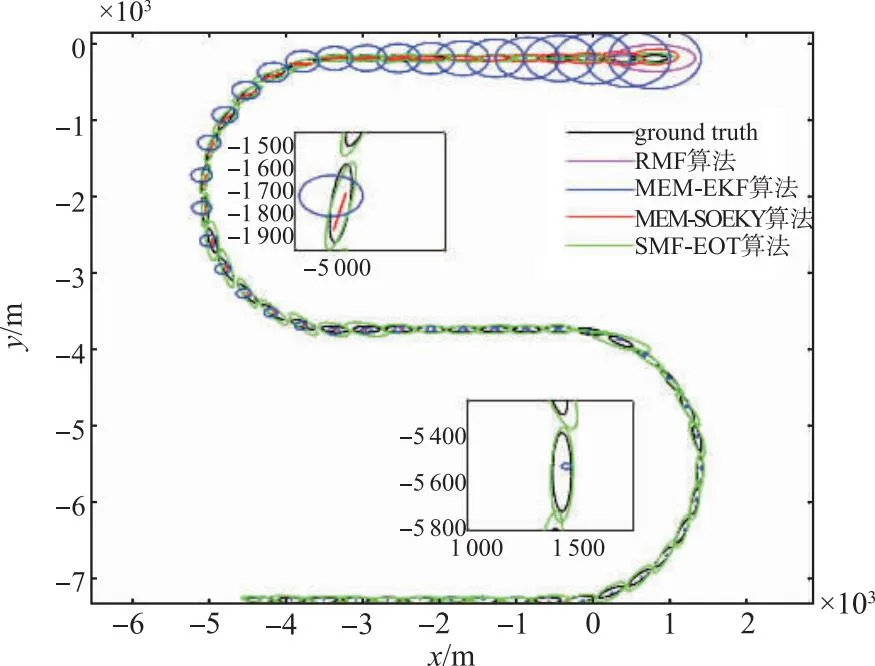
图4 4种算法扩展目标跟踪结果

图5为4种算法的位置和速度RMSE的100次Monte-Carlo实验仿真结果。可以看出,与MEM-EKF、MEM-SOEKF和RMF算法相比,本文所提出的SMF-EOT算法具有更小的位置RMSE。当目标机动时,MEM-EKF和RMF的位置和速度RMSE增大,主要是由于MEM-EKF和RMF算法假设的噪声统计特性与实际噪声不匹配,从而导致其位置和速度估计精度下降。虽然MEM-SOEKF算法通过二阶泰勒级数展开对非线性进行近似,在目标机动时估计精度并未下降,但该方法同样仅适用于噪声服从高斯分布的扩展目标跟踪系统,在UBB噪声条件下其位置和速度RMSE仍高于SMF-EOT算法。

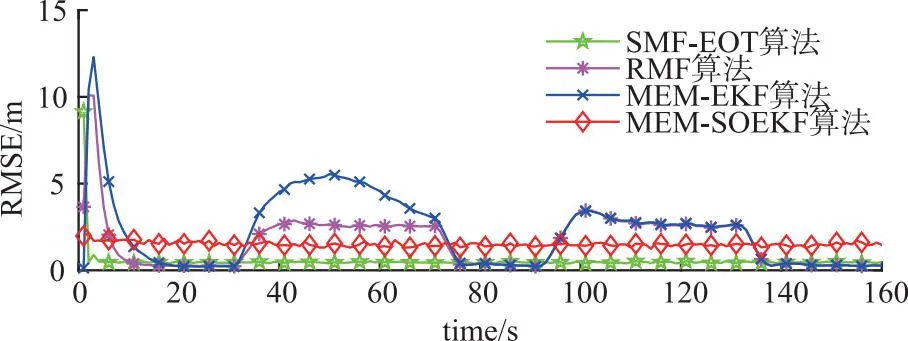
(a)位置

表1为4种算法的平均均方根误差(average root mean square error,ARMSE)。可以看出,所提算法的位置ARMSE相比与RMF、MEM-EKF和MEM-SOEKF算法分别提高了69.2%、77.05%、和65.74%;其速度ARMSE分别提高了49.69%、49.92%和48.7%。

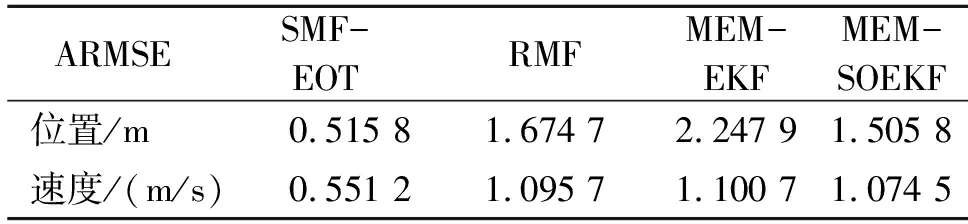
表1 4种算法的位置和速度ARMSE对比

为对四种算法目标扩展形态估计的准确度进行评价,采用高斯威斯顿距离(gaussian wasserstein distance,GWD)作为评价指标[23],该距离通过目标位置和形状误差计算目标扩展状态误差,其计算公式如下:

(50)

图6为4种算法100次Monte-Carlo实验下的GW距离。从图中可以看出,相比于MEM-EKF、MEM-SOEKF和RMF算法,本文所提算法具有更小的GW距离,且RMF算法估计性能较差。主要原因在于RMF算法将扩展形状建模为随机矩阵,导致迭代更新过程中无法处理椭圆长短半轴与角度之间的不确定性导致对目标扩展状态估计精度较低。虽然MEM-EKF和MEM-SOEKF比RMF算法对目标扩展状态估计精度较高,但在UBB噪声条件下受噪声适应性的影响其估计精度低于本文所提SMF-EOT算法。

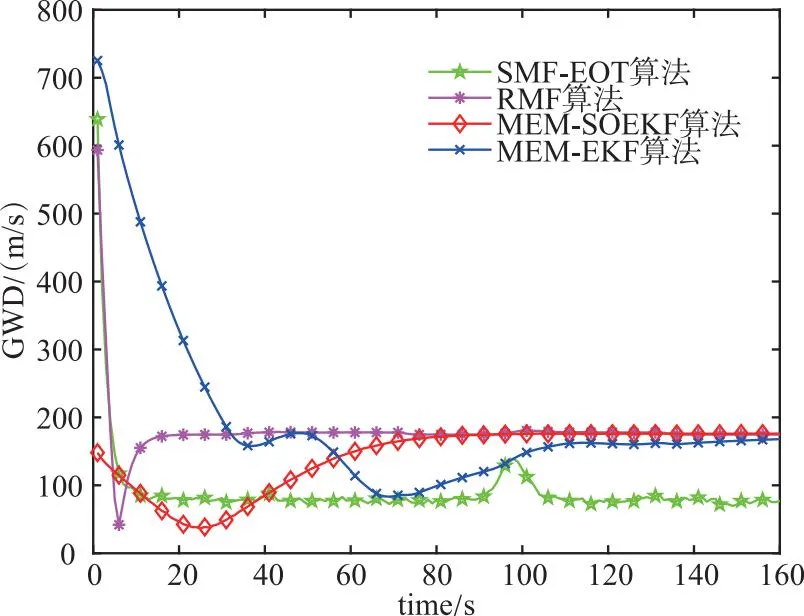
图6 4种算法的GW距离

表2为4种算法的(average Gaussian wasserstein distance,AGWD)对比,所提算法的AGWD相对于RMF、MEM-EKF和MEM-SOEKF分别提高了49.59%、54.43%和36.73%。

表2 4种算法的AGWD对比

3.2 参数影响分析

本文所提算法假设量测噪声为散射源与误差量测噪声集合的Minkowski和,初始参数散射因子λ以及量测误差噪声边界U可能会影响算法性能。

考虑量测误差噪声边界U=diag{202,102}时,散射因子λ分别为0.25、0.5和1对本文所提算法进行100次Monte-Carlo实验;散射因子λ=0.25时,量测误差噪声边界U分别为diag{202,102}、diag{1002,502}和diag{1502,1002}对本文所提算法进行100次Monte-Carlo实验。

图7为不同噪声影响参数λ下SMF-EOT算法位置RMSE和GW距离对比。从图中可以看出,影响参数λ值越小,SMF-EOT算法收敛性越好。

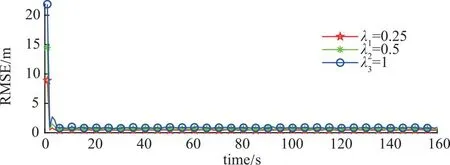
(a)位置

图8为量测误差噪声边界U下SMF-EOT算法位置RMSE和GW距离对比。可以看出量测误差噪声边界U越小,量测误差边界越小,SMF-EOT算法对目标运动和形态估计精度越高。

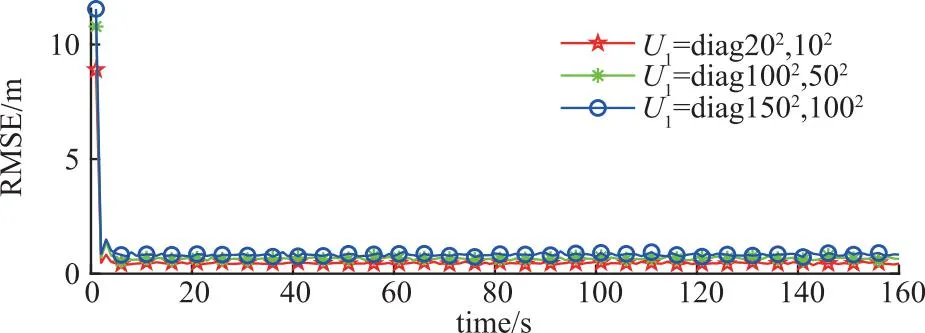
(a)位置

综上所述,在UBB噪声条件下,与MEM-EKF、MEM-SOEKF和RMF算法RMSE相比,本文所提SMF-EOT算法具有更小的位置、速度和椭圆GW距离,估计性能更好。主要原因在于SMF-EOT算法考虑噪声边界已知但其统计特性未知的扩展目标跟踪系统,假设系统噪声为UBB噪声并将其建模为椭球集合,利用集员估计理论以及椭球Minkowski差对目标运动和扩展状态进行估计。然而MEM-EKF、MEM-SOEKF和RMF算法使用贝叶斯规则迭代估计目标状态,噪声假设局限于高斯等随机分布,没有考虑到有界噪声的扩展目标跟踪问题导致其跟踪性能降低。

4 结语

本文针对有界噪声条件下的椭圆扩展目标跟踪问题,提出基于集员滤波的椭圆扩展目标跟踪方法。其将系统噪声建模为椭球集合噪声,采用集员滤波方法对目标运动状态进行估计,在对目标扩展状态估计时利用Minkowski和理论获取量测椭圆并用Graham scan算法对其进行融合,同时结合椭圆封闭形式的Minkowski差求解得到目标扩展状态。数值模拟仿真实验结果表明,在基于有界噪声假设的扩展目标跟踪系统中,本文所提算法对扩展目标运动状态和形态具有较高的估计精度。未来的研究方向可以考虑解决有界噪声条件下非凸形状扩展目标的跟踪问题。