基于组稀疏卡尔曼滤波的多步轨迹预测方法

王 娜,罗 亮,彭 锟,张鑫海

(1.天津工业大学控制科学与工程学院,天津,300387;2.天津市电气装备智能控制重点实验室,天津,300387;3.微光机电系统技术教育部重点实验室(天津大学),天津,300072)

多步轨迹预测即利用运动目标的历史轨迹信息构建预测模型,并输出该模型对运动目标未来多个时刻的轨迹估计值。目前的研究以模型法和深度学习为主,前者一般利用卡尔曼滤波及其改进为基础来构建预测模型。如文献[1]提出的基于传统卡尔曼滤波(Kalman filtering,KF) 的飞行轨迹预测方法。相比传统卡尔曼滤波,扩展卡尔曼滤波能够有效处理非线性模型的估计,如文献[2]基于扩展卡尔曼滤波(extended Kalman filtering,EKF)实现对不确定情况下的无人驾驶车辆的轨迹预测;文献[3]基于扩展卡尔曼滤波方法和差分自回归滑动平均模型对上海中心大厦实测加速度幅值数据的实时变化趋势进行预测。相比前两类滤波方法,文献[4]所提的多项式卡尔曼滤波方法能够有效针对信息缺失、非线性、多机动情况,过程较为简单,计算效率高,机动自适应较强,但通常易受模型误差和数据噪声影响,对于复杂的运动目标轨迹预测精度不高。上述卡尔曼滤波方法主要基于单模型法,所构建的运动模型存在数据处理难度大及预测精度低等问题,对此文献[5]提出改进的交互式多模型轨迹预测算法。此外,上述卡尔曼滤波类方法由于只能输出一步预测的估计值,故难以单独应用于多步预测中。

与传统模型法基于参数构建的思想不同,神经网络基于数据驱动实现自主学习,对于数据特性考虑较为全面,可以实现复杂非线性时间序列的准确、多步预测。浅层学习神经网络中,文献[6]在BP神经网络基础上,引入双三角函数变换思想,实现对船舶轨迹的精确预测;文献[7]利用改进的狼群算法优化径向基神经网络学习过程,实现对无人艇动态障碍物的航行轨迹预测。深度学习方法不依赖运动目标的机理特性,数据容易获得,且可利用历史数据进行中长期轨迹预测,预测时间长且精度较高,故得到广泛应用。如文献[8]利用长短时记忆网络(long short-term memory,LSTM)与一维卷积神经网络(one-dimensional convolutional neural network,1DCNN)结合,实现对导弹轨迹的预测。文献[9]利用门控循环单元网络(gated recurrent unit,GRU)进行飞机轨迹预测,与传统的循环神经网络(recurrent neural network,RNN)和反向传播网络(back propagation,BP)相比,预测性能更优。文献[10]引入双向传播机制和Mogrifier数据耦合模块,改进传统GRU网络,使其预测性能进一步提高。综上所述,神经网络类方法能够较充分继承历史信息,更适合处理时间序列的预测,但其内部参数较多,训练耗时,且随着时间序列的数量级增加,很容易出现梯度消失和梯度爆炸问题。

此外,神经网络自身的结构和参数的确定受人为因素影响而缺乏客观依据,因而导致预测误差偏大,泛化能力较差。相比神经网络,稀疏编码(sparse coding,SC)能以少量的输入特征矩阵与稀疏向量的加权和形式对原始输出数据矩阵进行重构,无需人为调节参数,计算过程简单,效率较高[11]。但稀疏编码直接用于多步预测时,求解稀疏向量时计算量较大,为此,组稀疏编码(group sparse coding,GSC)把输入和输出的系数矩阵以对角矩阵形式表示,仅通过一次计算即可输出多个稀疏向量,有效降低了计算量,简化了多步预测的计算过程[12]。目前稀疏编码类方法通常用于结构健康检测和图像处理等领域,而在轨迹预测领域的应用较少,如文献[13]针对Lamb波边界反射引起的码间串扰问题,采用移不变稀疏编码方法进行信息恢复,提出了基于Lamb波的数据传输与缺陷检测同步实现方法;文献[14]针对在小样本人脸表情数据库上识别模型过拟合问题,提出基于特征优选和字典优化的组稀疏表示分类方法。

综上所述,本文将组稀疏编码[15]与卡尔曼滤波结合,提出了一种基于组稀疏卡尔曼滤波的多步轨迹预测方法(multi-step trajectory prediction method via group sparse Kalman filtering,MSTPM-GSKF)。

1 超前T步轨迹预测问题描述

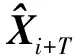
(1)

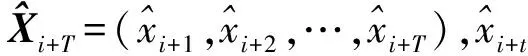
2 GSC的基本原理

2.1 SC基本原理

给定轨迹序列Xg,稀疏编码是以稀疏向量α和输入特征矩阵D乘积的线性组合表示对应的输出特征矩阵X[16],即:

(2)

式中:X=[x1,x2,…,xp]T,xi为X中第i个轨迹点,i=1,2,…,p,p为轨迹点个数;D=[d1,d2,…,dM],di=[xi1,xi2,…,xip]T为D中的第i个列向量,i=1,2,…,M,M为D中列向量集合的个数,xij为di中第j个轨迹点,j=1,2,…,p;α=[α1,α2,…,αM]T为稀疏向量,αi为α中第i个稀疏系数,i=1,2,…,M。

稀疏编码中,给定输入特征矩阵D,稀疏向量α直接影响着输出特征矩阵X的精确性,因此对它的求解尤为重要,一般通过松弛算法转化为优化问题求解[17]:

(3)

式中:λ为惩罚参数。

对于α的求解,传统最小二乘(least square,LS)算法过程较简单,但LS对于输入多重共线性及输入变量数大于数据个数等特殊情况,难以获得稳定解[18],且求解效率较低。对此,最小角回归算法(least angle regression,LAR)在误差平方和函数中加入1范数,可以递阶地获得重要输入变量,提高特征选择的准确性,有效改善上述问题,故本文采用LAR方法求解[15]。

LAR算法的基本思想如下:首先根据余弦相似度函数计算每个输入特征向量与输出特征向量的相关性,根据最大相关性值获得对应的输入特征向量,然后计算所有剩余的输入特征向量与当前残差向量的相关系数,从中筛选出绝对值最大的相关系数,选择其对应的输入特征向量,并将其与第一个获得的输入特征向量组合,获取其角平分线,并在该角平分线方向继续选择输入,直至所有输入被选择完毕,其原理如下:

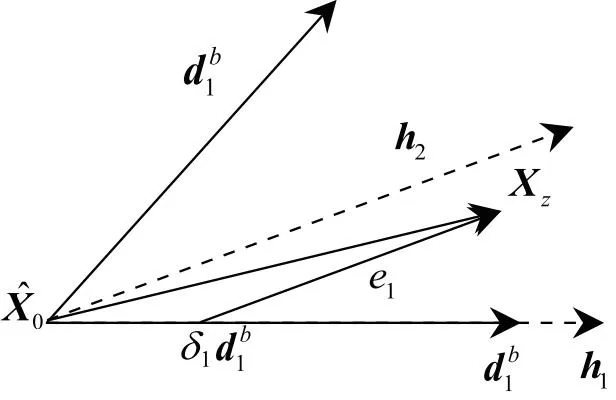
图1 最小角回归原理

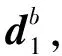
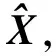
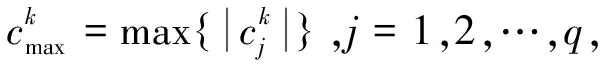
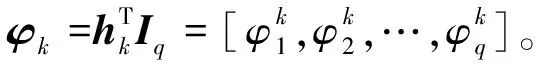
Step7计算搜索步长

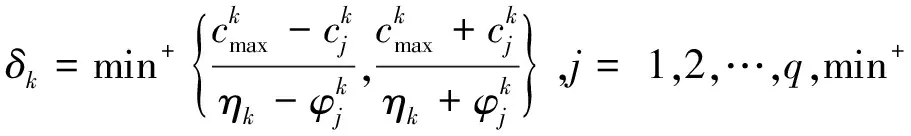
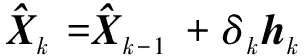
2.2 GSC基本原理

组稀疏编码是将多个输入特征矩阵和输出特征矩阵排列成对角矩阵形式的线性组合,从而对输出特征矩阵进行稀疏表示的过程[12]:

(4)

式中:Di为第i个输入特征矩阵;Xi为Di对应的输出特征矩阵;αi为对应的第i个稀疏向量,i=1,2,…,J,J为输入或输出特征矩阵的个数。

3 IKF基本原理

(5)

式中:F为状态转移矩阵;k为迭代次数。

一步预测协方差阵P(k/k-1)为:

P(k/k-1)=FP(k/k-1)FT+Q

(6)

Q为过程协方差阵,则卡尔曼增益矩阵K(k)为:

(7)

其中H为观测矩阵,S(k)为:

(8)

最后协方差阵P(k/k)更新为:

P(k/k)=[In-K(k+1)H]P(k/k-1)

(9)

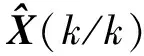
(10)

其中V(k)为残差,即:

(11)

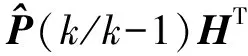
当得到k时刻预测误差与k-1时刻残差的比例关系后,可利用V(k-1)对预测值进行修正,故本文进行以下改进:

1)将式(7)的S(k)-1替换为S(k-1)-1,获得式(12):

(12)

2)把式(10)中V(k)替换为V(k-1),获得式(13):

(13)

将式(13)替换式(10),并将式(12)置于式(7)之后,其余步骤同原基本卡尔曼滤波算法。

上述改进的优点在于,在原KF算法中,式(10)的结果是对当前状态的最优估计,而改进后,用式(13)得到的结果为目标状态修正后的超前一步预测值,该结果相比前者更加符合状态预测的意义。

4 MSTPM-GSKF算法描述

针对多步轨迹预测问题,本文提出一种基于组稀疏卡尔曼滤波的多步轨迹预测方法MSTPM-GSKF,首先利用组稀疏编码直接输出多步预测结果,避免了迭代多步中预测误差的累计,及繁琐的调参以及模型训练过程,然后与IKF结合,修正其预测值,输出最终的预测结果,具体过程如下:

首先为方便起见,仅考虑单维坐标系的情况,给定该坐标系下的m个输入数据,建立超前T步预测模型,如图2所示。

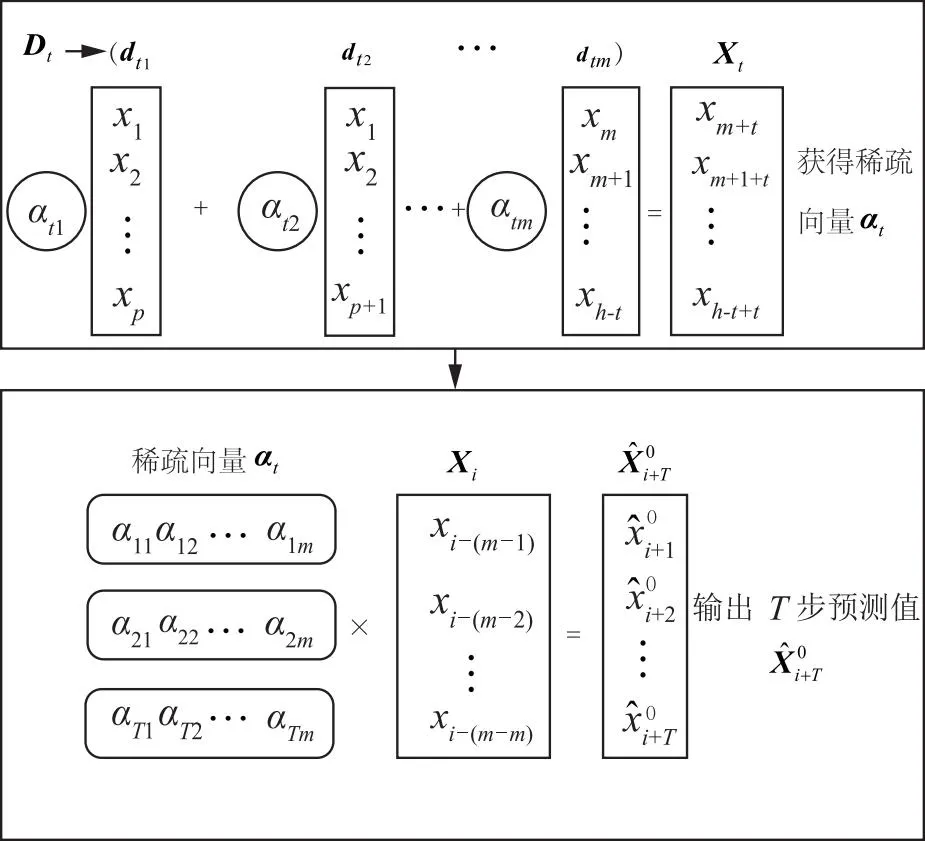
图2 基于GSC的超前T步预测基本原理

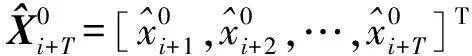
图2的具体过程如下:首先,利用窗口长度为m,滑动步长为1的滑动窗口根据不同的预测时间间隔t,将h-t个轨迹数据划分为多个轨迹序列,其序列个数为p=h-t-m+1,进而按时间顺序进行排列,构成对应的输入特征矩阵Dt:

(14)

其次,根据输入数据进行时间间隔为t的时间延迟,构建对应的输出特征向量Xt:

Xt=[xm+t,xm+1+t,…,xh]T

(15)

再次,利用所构建的T个Xt及Dt进行组稀疏编码,并将所求解的稀疏向量αt按顺序排列,构成系数矩阵A:

A=[a1,a2,…,aT]T

(16)

由卡尔曼滤波的计算过程可发现,当输入数据为m×1的列向量时,其输出也应为m×1的列向量,故其状态转移矩阵F应为m×m的方阵,且当预测步长为T时,为保证输入输出数据个数一致,即预测步长最大为T=m,因此,本节对于状态转移矩阵的建立如下。

对于单步预测,即预测步长T=1时,状态转移矩阵A为:

(17)

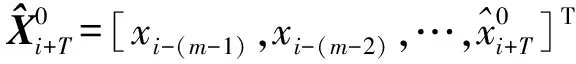
对于两步预测,即预测步长T=2时,状态转移矩阵A为:

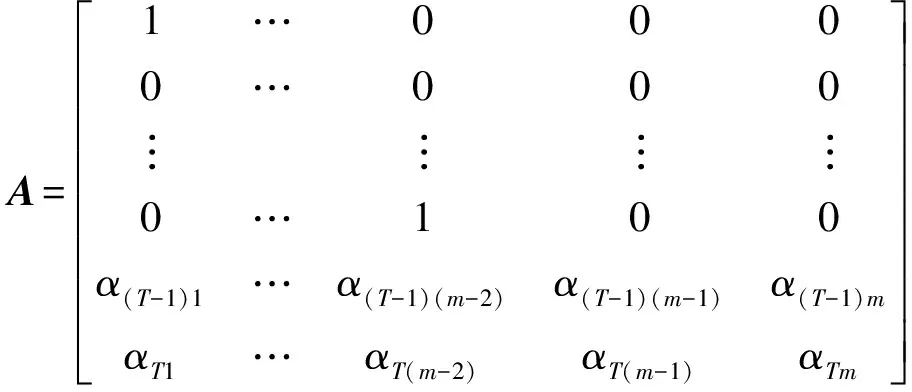
(18)

(19)

综上所述,基于MSTPM-GSKF的多步轨迹预测方法如下:

Step1采集机动目标在单维坐标系下的h个历史轨迹数据Xg={x1,x2,…,xh}。

Step2针对不同预测时间间隔t,构建输入特征矩阵Dt及其相应的输出特征向量Xt。

Step3利用GSC求解稀疏向量αt,构成系数矩阵A,建立T步预测模型。

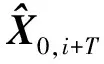
图3 基于MSTPM-GSKF的多步轨迹预测流程图

5 仿真研究

本文利用X-Y-Z三维坐标系下的非线性函数轨迹验证所提方法对机动目标轨迹预测的有效性,其参数方程如下:

(20)

其中0≤t≤10π,时间点数量为1 000个,时间间隔为0.01π,坐标单位为m,取前800个数据点作为训练集来构建预测模型,后200个数据点作为测试集来输出预测结果。分别在X、Y、Z方向上,对每一维的轨迹进行多步预测,最后组成三维空间的预测轨迹。

预测误差指标采用均方根误差(root mean square error,RMSE):

(21)

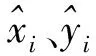
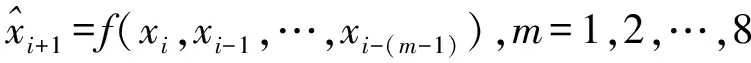
表1 m=2～8时MSTPM-GSKF的单步预测误差比较

由表1可知,在轨迹点个数m=6时轨迹预测的均方根误差最低,为0.003 3 m。当m=7和8时,随着输入轨迹点的增加,预测的均方根误差均保持不变,仍为0.003 3 m,故可以确定,当m=6作为系统输入较适宜。

输入个数为6时,将预测步长从1增加到6,获得轨迹的预测均方根误差如表2所示。

表2 m=6时MSTPM-GSKF方法的多步预测误差比较

由表2可知,在预测步长均匀增加下,所提方法的预测RMSE也随之增加,如步长T=1增加到T=2时,预测误差由3.3 mm增加到5.1 mm,增加了1.8 mm。步长T=2增加到T=3时,预测误差增加了1.9 mm,而且随着预测步长的增加,预测误差逐渐增加,在T=4时,误差精度为10-3m,之后随输入个数增加,预测误差逐渐增加,但仍保持在10-2m左右。因此,预测步长为4是预测误差变化趋势的重要转折点,但为便于和LSTM等其他神经网络方法作仿真比较,这里取预测步长T=m=6。

为验证m=6,T=6时所提方法的鲁棒性,对测试数据集依次添加1～100 dB信噪比的高斯白噪声,输出的轨迹预测误差曲线如图4所示。

图4 MSTPM-GSKF方法在不同信噪比下的轨迹预测误差

由图4可知,随着信噪比的增加,MSTPM-GSKF方法的轨迹预测误差逐渐降低,当取信噪比为1 dB时,预测误差最大,为1 846 mm;信噪比为20 dB时预测误差为284 mm,误差曲线开始变得平缓,在信噪比为40 dB时预测误差为52 mm,误差曲线进一步平缓;之后,信噪比在60～100 dB范围内,预测误差曲线进入稳定状态,预测误差的值基本不变,为16 mm左右,体现出本方法在由低到高的信噪比变化下,具有较强的鲁棒性,而且收敛速度较快。

为进一步验证所提方法的有效性,设m=6,T=6下,将GSC、BP、LSTM和所提MSTPM-GSKF在X、Y、Z单轴及整体预测RMSE进行比较,见表3,BP和LSTM网络的学习率η取0.1,训练次数取500。

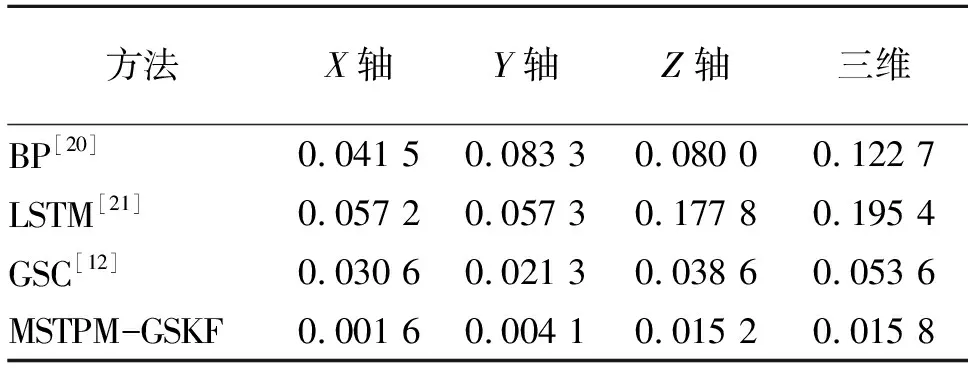
表3 BP、LSTM、GSC和MSTPM-GSKF在X、Y、Z轴及整体预测误差的比较 单位:m

表3可见,和其他3种方法相比,所提MSTPM-GSKF方法预测误差均为最小,在X、Y、Z轴的RMSE分别为1.6 mm、4.1 mm、15.2 mm,预测精度最高为10-3m,最低为10-2m,而GSC方法的预测精度最高和最低均为10-2m,BP网络的预测精度最高为10-2m,最低为10-1m,LSTM网络的预测精度最高为10-2m,最低为10-1m。通过上述比较可知,所提方法在单轴和三维坐标系下的预测精度均较高,显示出它的有效性。

分析原因,这是因为BP和LSTM神经网络中,内部采用tanh和sigmoid激活函数,待调参数较多,如神经元个数、学习率、批次等,而训练结果的准确性直接受参数的影响,当某次训练时这些参数选取不当而导致训练结果不佳时,只能试凑选取新的参数进行下一次训练。这种试凑选择的主观性易导致训练结果不稳定,甚至会难以收敛。

而GSC只需要计算稀疏向量的系数α即可确定最终输出结果,α采用最小角回归算法估计求解,一般给定初值后,通过简单的计算,即可获得稳定的全局解,避免了BP和LSTM中由于初值选取和试凑选择的主观性而易于陷入局部极值的情况,确保了结果的准确性,因此预测误差较小。所提MSTPM-GSKF方法在预测中,利用IKF的修正过程对GSC的预测结果进行误差补偿,因此预测精度高于GSC,在上述方法中预测性能最好。

结合本文第4节关于所提MSTPM-GSKF方法的稳定和收敛性证明,作进一步的仿真验证,在输入个数为6,预测步长为6时,获得BP、LSTM、GSC和MSTPM-GSKF的三维轨迹预测结果,受输入个数选取所限,实际轨迹点取198个,见图5。

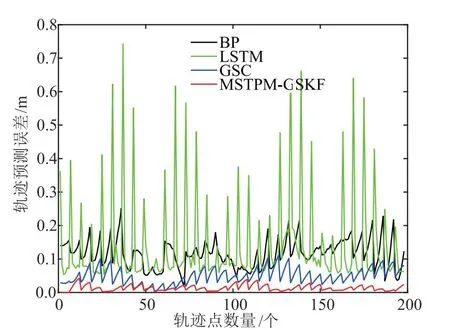
图5 BP、LSTM、GSC和MSTPM-GSKF在198个轨迹点下的三维轨迹预测误差

由图5可知不同方法在每个轨迹点的预测误差均具有一定波动性,其中LSTM的波动性最大,BP次之,然后是GSC方法,所提MSTPM-GSKF方法的波动性最小,说明它具有较高稳定性。

此外,本文为进一步加强稳定性的验证,采用均值和方差指标来评价上述方法的预测稳定性,各方法的指标比较见表4。

表4 GSC、LSTM、GRU和MSTPM-GSKF方法轨迹预测误差的均值和方差比较

由表4可知,所提MSTPM-GSKF方法的均值为0.013 3 m,方差为0.000 07 m2,远远低于其他3种方法,具有较高的稳定性。

X-Y-Z三维坐标系下,上述4种方法的预测轨迹和实际轨迹的对比如图6所示。

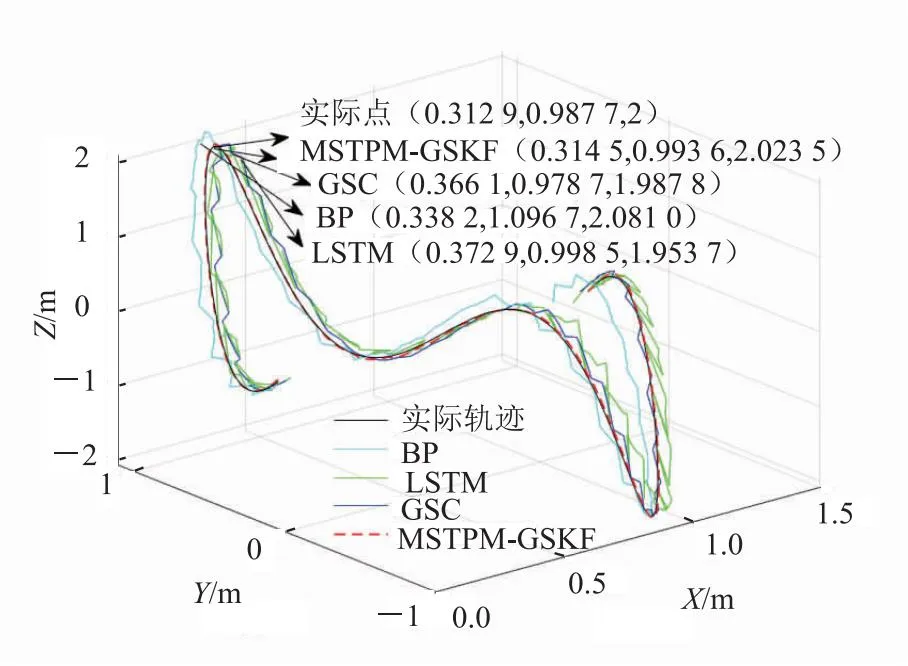
图6 BP、LSTM、GSC和MSTPM-GSKF的三维轨迹多步预测结果比较

由图6可知,在机动性较强的实际点(0.312 9,0.987 7,2)处,BP法预测值为(0.338 2,1.096 7,2.081 0),距该点距离为0.138 1 m;LSTM法预测值为(0.372 9,0.998 5,1.953 7),距该点距离为0.076 6;GSC预测为(0.366 1,0.978 7,1.987 8),距该点距离为0.055 4。而本文所提方法MSTPM-GSKF的预测结果为(0.314 5,0.993 6,2.023 5),距该点距离仅为0.024 3 m,在3种方法中预测误差最小,对于具有较强机动性运动目标的适应能力较好,故预测性能最好。

6 结语

本文首先利用LAR算法一次直接求解稀疏编码方法中的稀疏系数,并且结合卡尔曼滤波一次学习多步预测过程,然后利用改进卡尔曼滤波来修正预测结果,确保其精确性,形成了基于组稀疏卡尔曼滤波的多步轨迹预测方法,最后通过与传统浅层、深度学习神经网络和组稀疏编码方法的仿真比较,验证了所提方法的有效性。

本方法不仅在建模时避免了人为因素对模型结构的影响,而且在预测中,当待预测目标的运动特性与所用训练数据的特性相差较大时,BP和LSTM依然根据此训练模型进行预测,参数失配会导致较大的预测误差,而本方法利用改进卡尔曼滤波对组稀疏编码的预测值进行了动态修正,有效减小了建模误差产生的影响。因此对于机动目标的运动轨迹具有较强的预测性能。