偶极SLEκ迹与圆盘相交的概率估计*

牛冰洁， 蓝师义

广西民族大学数学与物理学院，广西 南宁 530006

随机Loewner演变，简称SLE，是由Schramm（2000）研究环路消除游走与一致生成树的尺度极限时引入的一类平面随机曲线的连续增长过程.这个增长过程是由驱动项为一个时间改变的一维Brownian运动的经典Loewner 微分方程的解来描述.该SLE 过程与统计力学中很多离散统计模型的尺度极限密切相关.Smirnov（2001）证明了三角形格上的临界渗流探索过程的尺度收敛于SLE6；Lawler et al.（2002b）猜测自回避游走尺度收敛于SLE83，Gwynne et al.（2021）证明了Liouville量子重力曲面上这个收敛性；Chelkak et al.（2012；2015）证明了Ising 模型尺度收敛于SLE3；Smirnov（2007；2010）证明了q= 2 的团簇模型尺度收敛于SLE163；Lawler et al.（2004）证明了环路消除游走尺度收敛于SLE2以及一致生成树的Peano曲线尺度收敛于SLE8；以及Schramm et al.（2005；2009）证明了调和探索过程与离散高斯自由场分别尺度收敛于SLE4等.同时，SLE 使得Mandelbrot 关于Brownian 运动边界的Hausdorff 维数的猜测（Lawler et al.，2001a）与平面Brownian 运动相交指数值的决定（Lawler et al.，2001b； Lawler et al.，2001c； Lawler et al.，2002a）等问题的解决是它最成功之一.SLE 具有多个不同的版本，其中最常见的有下面3 种类型：一是通弦SLE，其迹是单连通区域内从一个边界点到另一个边界点的一条随机增长曲线；二是径向SLE，其迹是从单连通区域的一个边界点到该区域一个内点的一条随机增长曲线；三是偶极SLE，其迹的演化是从单连通区域的一个边界点到不包含该边界点的一个边界弧段.有关更多SLE 的基本理论与背景知识可参见（Kager et al.，2004； Lawler 2005； Marshall et al.，2005）.

对于上半平面内通弦SLEκ，基于它所满足通弦Loewner 微分方程，Beffara（2008）已经导出了上半平面内通弦SLEκ迹与圆盘相交的概率表达式.本文将研究偶极SLEκ过程的相应问题，即偶极SLEκ迹与圆盘相交的概率估计.很自然地，可以按照（Beffara，2008）的方法直接讨论带形区域内偶极SLEκ迹与圆盘相交的概率问题，但这并不起作用，主要原因是利用带形区域内偶极Loewner微分方程导致计算量太复杂.然而，我们发现若能先求出上半平面内偶极SLEκ迹与圆盘相交的概率估计；然后，将带形区域共形映射到上半平面上，由偶极SLEκ的共形不变性这个问题可以解决.本文的主要结果如下.

第一，导出上半平面内偶极SLEκ迹与圆盘相交的概率估计，即：

定理1 固定0 <κ< 8，假设γ是上半平面H 内从1 到（-∞，0］的偶极SLEκ过程{ft(z)}的迹.令点z0∈H，α(z0) ∈( 0，π )是z0的幅角，则对所有ε > 0，当κ∈(0，8)时有下面表达式

这里B(z0，ε)表示以z0为圆心ε为半径的圆盘；符号≍表示每一边都小于或等于某个常数乘以另一边，它在下文的含义相同.

证明定理1 的方法是先给出上半平面偶极SLEκ过程所满足的偶极Loewner 微分方程（见引理1），然后，基于该微分方程按照（Beffara，2008）的方法来讨论.更具体地，对于0 <κ< 8，令{ }ft表示上半平面H内从1到（-∞，0］的一个偶极SLEκ过程，且它的壳Kt与迹γt的定义分别见文后的式(7)～(8).设z0为H内的某一个固定点，且δt为z0与壳Kt之间的欧氏距离.应用共形变换与Koebe 1/4定理得到δt的一个估计式.同时，把H Kt共形映射到单位圆盘内，且将直线R 上相关的驱动过程变换成单位圆周上的一个驱动过程其中αs为( )0，2π 内的一个扩散过程.对αs应用Girsanov变换并结合δt的估计式，可推出迹γ相交于圆盘的概率与αs在区间(0，2 )π 内存活概率是等价的，由后者的结果得到式(1)成立.

第二，给出带形区域内偶极SLEκ迹与圆盘相交的概率估计，即：

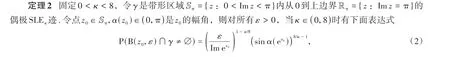
其中B(z0，ε)表示Sπ内以z0为圆心ε为半径的圆盘；符号≍的含义如同在定理1.

证明定理2的方法是通过共形映射将带形区域内的偶极SLEκ变成上半平面内的偶极SLEκ.然后，根据偶极SLEκ的共形不变性由定理1 的结果，得到带形区域内偶极SLEκ迹与圆盘相交的概率表达式(2)成立.这将上平面内通弦SLEκ过程相应的概率估计推广到了偶极SLEκ的情形.

值得指出，虽然证明定理1 与定理2 的方法类似于（Beffara，2008）的技术，但是，由于所考虑的方程和区域不同于（Beffara，2008），因此，所涉及的很多细节是不一样的.

1 预备知识

简要介绍本文涉及的通弦与偶极SLEκ的基本概念，更详细的相关背景知识可参见（Bauer et al.，2005；Lawler，2005；Kemppainen，2017）等.

1.1 通弦SLEκ

上半平面内的通弦SLEκ：令H ≔{z∈C ：Imz> 0}表示上半平面，这里C 是复平面.设κ> 0是一个实参数，Bt(0 ≤t< +∞)是实轴R 上从B0= 0 开始的一维标准Brownian 运动.对任意z∈Hˉ{0}，考虑Loewner微分方程

其中z从上半平面H内趋近于0.已经知道γ几乎肯定是一条从原点到无穷远点的连续路径.

任意区域内的通弦SLEκ：假设D⊊C 是任意一个单连通区域，则Riemann 映射定理给出，存在一个共形映射ϕ：D→H.设ϕt是Loewner方程(3)的解，初始条件为ϕ0(z)=ϕ(z)，z∈D，则过程{ϕt：t≥0}称为在映射ϕ下单连通区域D内的通弦SLEκ.易知ϕt=gt∘ϕ，其中gt是方程(3)的解.如果γt是过程{gt}的迹，则过程{ϕt}的迹是ϕ-1(γt)，它是D内一条从D的一个边界点到另一个边界点的路径.

1.2 偶极SLEκ

带形区域内的偶极SLEκ：考虑带形区域Sπ={z∈C ：0 < Imz< π}.则Sπ内的偶极SLEκ定义为下面偶极Loewner微分方程的解

已经知道，Sπ内偶极SLEκ的迹γt是从0到边界Rπ的一簇随机曲线.

注1 Beffara（2008）已经给出了通弦SLEκ迹与圆盘相交的概率表达式；在本文将讨论偶极SLEκ迹与圆盘相交的概率估计（定理1与定理2）.

2 几个引理

其中Bt如同前面是一个一维的标准Brownian运动.

证明 由Koebe 1/4定理可推出该引理成立，具体可参见推论3.19（Lawler，2005）.证毕

如同前面，设Bt是一个标准的Brownian 运动，Ft= σ{Bs：0 ≤s≤t}是由Brownian 运动产生的滤子.假设Mt是下面随机微分方程的非负解：

并记λ为它的特征值.则这个扩散过程Xt在时间t之前不碰到边界的概率为

符号≍的含义如同前面.

3 相交概率估计

上半平面内通弦SLEκ迹与圆盘相交的概率表达式已经在（Beffara，2008）中给出.在这一节基于偶极Loewner微分方程(9)并结合引理1～4，首先给出了定理1的证明.其次，应用带形区域Sπ与上半平面H 之间的共形变换，由偶极SLEκ共形不变性与定理1的结果，可以推出定理2成立.

将应用引理3 导出满足方程(19)的αs与满足方程(20)的αs具有相同分布.所以，下面只需考虑前者就足够了.

事实上，根据方程(19)得

这结合式(25)与ω0的定义可推出式(2)成立.因此，完成了这个定理的证明.证毕