一类时滞分数阶Volterra微积分方程组的严格误差分析*

郑伟珊

韩山师范学院数学与统计学院， 广东 潮州521041

我们研究的分数阶时滞Volterra微积分方程组形式如下：

这里τ∈[0，T]，0 <γ< 1，Dγ和Γ 分别表示Caputo 分数阶求导算子和Gamma 函数，并已知核函数K͂和源函数G是给定的函数.假定这些函数都在对应的定义域上充分光滑.延迟项是ψ(τ)并满足：

Volterra 型方程常用于描述捕食系统中掠食者与猎物进行互动时的动力学行为，一直备受广泛关注.关于谱配置方法研究Volterra 积分方程，汤涛院士首次采用Legendre 谱配置方法研究Volterr 积分方程（Tang et al.，2008），随后与陈艳萍教授合作探讨解充分光滑条件下的弱奇异Volterra 积分方程（Chen et al.，2009）和解非充分光滑的弱奇异Volterra积分方程（Chen et al.，2010），提出并分析了一种高精度的Jacobi谱配置方法，并引起了大量相关后续研究（Wei et al.，2012；Zhang et al.，2013；Tohidi et al.，2014；Yang et al.，2014；Gu，2016；Cai et al.，2018；Gu，2020；Zheng，2021），这些研究皆基于谱分析具有显著的误差指数收敛性.近年分数阶方程发展迅速，由于其具有广泛的应用背景，诸如反应扩散问题、吸烟模型、疾病传播等（Zeng et al.，2014；Khan et al.，2019；Shah et al.，2020），Volterra 型方程的研究也逐步迈向分数阶领域（Yang et al.，2014；Cai et al.，2018），然而发展缓慢，特别是考虑时滞因素的成果几乎没有，事实上时滞因素普遍存在，故本文将对一般时滞分数阶Volterra 微积分方程组进行严格的误差分析，为此需要进行如下变量变换，令

下面介绍下文的组织结构，第1节中给出一些有用的引理，这些引理对第2节的收敛性分析起着关键的作用，最后一节以一个数值例子验证理论分析的正确性.需要指出的是通篇文章中C表示一个独立于N的正的常数，但它依赖于给定的函数.

1 重要引理

2 误差估计

解，当ρ∈(0，1)时为近似分数阶导数.定义eρ(t) =Dρ f(t) -Uρ(t)为误差函数，其中e0(t) =e(t).若N充分大，则有如下结论

下面逐项估计Ij(t)，j= 0，1，2，3，4.利用式（19）和引理2可得

3 数值实验

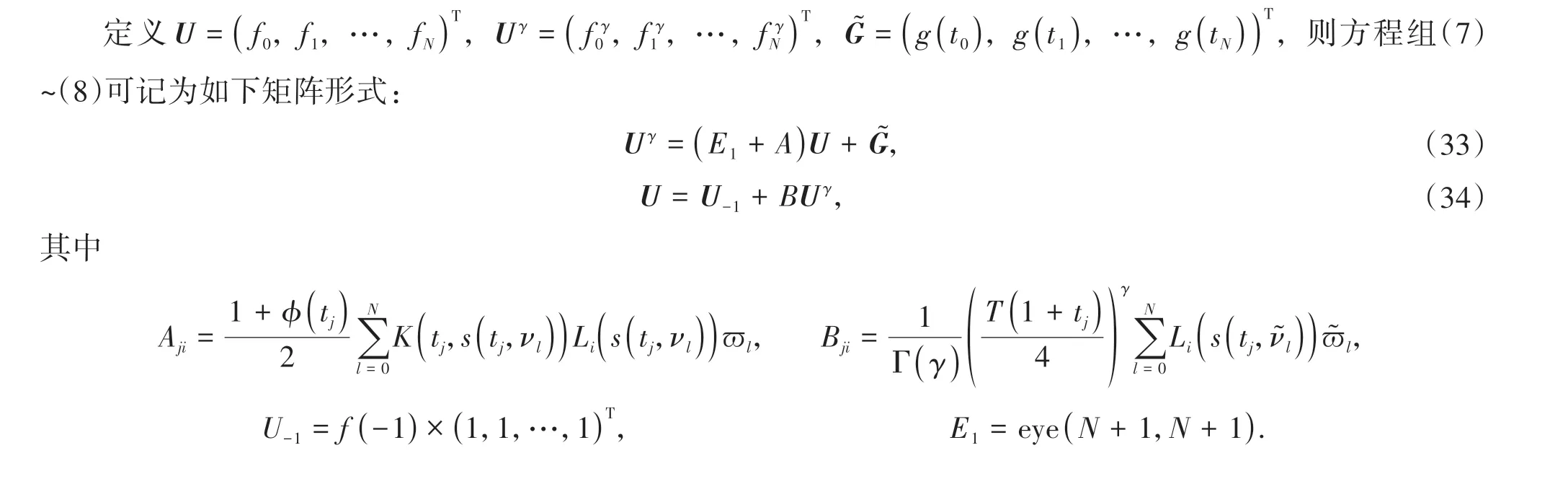
表1 f - U的L∞误差和L2ϖ-r，- r误差Table 1 The errors of f - U in L∞ and L2ϖ-r，- r norms

表2Dγ f -Uγ的L∞误差和L2ϖ-r，- r误差Table 2The errorsofDγ f-Uγ in L∞andL2ϖ-r，-r norms

为了可视化展示误差的指数衰减性，借助图形进行描述.图1是数值误差Dρ f-Uρ的L∞误差和L误差，这里2 ≤N≤20，从图形上可以一目了然发现误差呈指数衰减.同时将精确解与近似解、精确分数阶导数与近似分数阶导数进行绘图（见图2），从中发现它们分别高度一致，这更进一步验证了本文的结论.

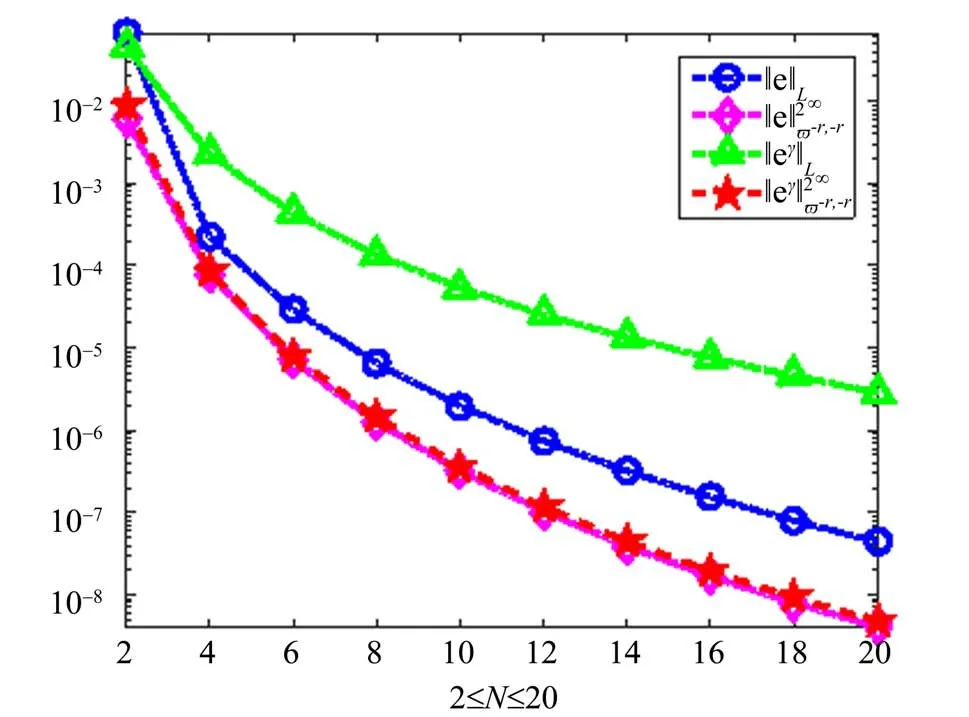
图1 Dρ f-Uρ在不同配置点下的L∞误差和L2ϖ-r，-r误差比Fig.1theerrorsofDρ f-Uρversusdifferentcollocation points in L∞ and L2ϖ-r， - r norms

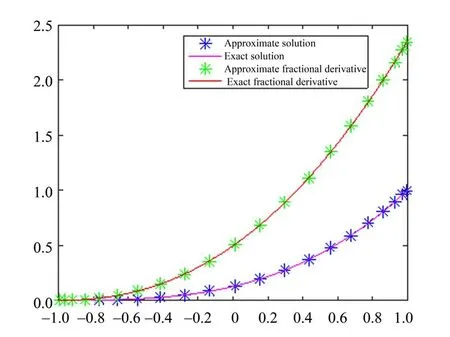
图2 精确解/精确分数阶导数与近似解/近似分数阶导数的对比Fig.2 Comparison between exact solution/exact fractional derivative and approximate solution/approximate fractional derivative