抛物线中的定值、最值问题探究——以2017年遵义市中考数学第27题为例

包胜利

(通渭县陇川学校,甘肃 定西 743319)

初中最值问题大致分为几何最值和代数最值两类.几何最值是指在一定条件下,求几何图形中某个确定的几何量(如长度、角度、面积等)的最大值或最小值,而代数最值是指求一些简单的代数式或与实际问题相关(如用料最省、成本最低、能耗最少、产值最高、利润最高等)的问题.

1 几何最值问题的求解思路

在初中阶段,解决几何最值问题的依据有两个,一是两点之间,线段最短;二是垂线段最短.由这两个依据延伸出以下常用的结论:三角形任意两边之和大于第三边,任意两边之差小于第三边;过圆内一点的所有弦中,垂直于过这点的直径的弦最短;直径是圆中最长的弦.

因此,几何方法求最值的思路是:将几何图形中的最值转化成基本的几何模型——“两点之间,线段最短”和“垂线段最短”.其关键是抓住运动变化中不变的相关量(长度、角度、面积)与变化的相关量比较大小.即通过平移、旋转、轴对称将多条线段首尾相连转化到两定点之间的线段上,实现“折”转“直”,利用“两点之间,线段最短”说明最小.或者将问题转化为一定点到一条定直线的距离, 利用“垂线段最短”即可得出最小值.

2 几何最值案例分析

2.1 试题呈现

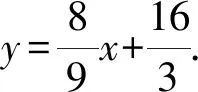
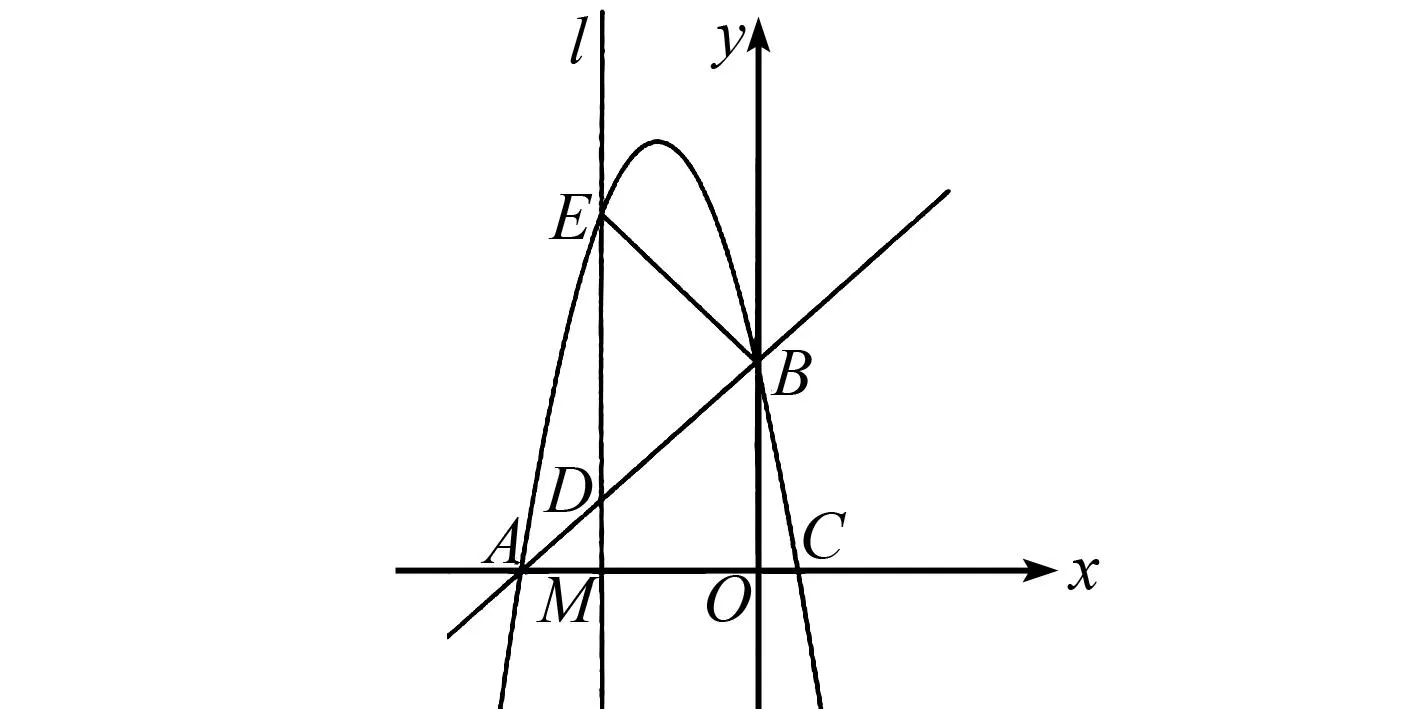
图1 中考题图

(1)求该抛物线的解析式与C点坐标.

(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D,E两点,当m为何值时,ΔBDE恰好是以DE为底边的等腰三角形[1]?

(3)在(2)问条件下,当ΔBDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间).

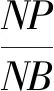
2.2 探究实验

第(2)问:如图2,拖动点M,观察BE和BD测量值的变化,是否存在相等的情形,有几种情况?

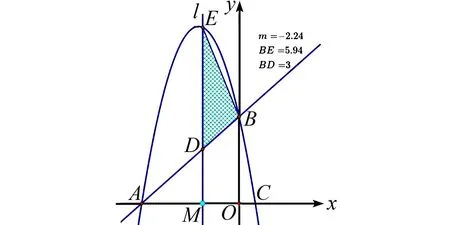
图2 探究等腰三角形

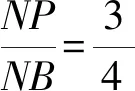
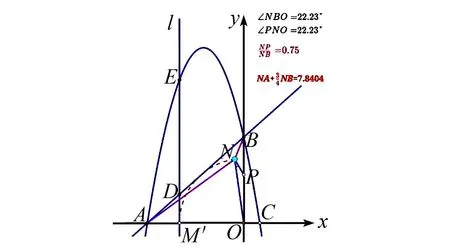
图3 探究最小值问题

2.3 思路分析

(1)根据已知条件求出A,B坐标, 用待定系数法可求出抛物线解析式.

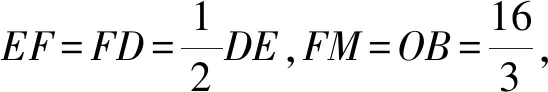
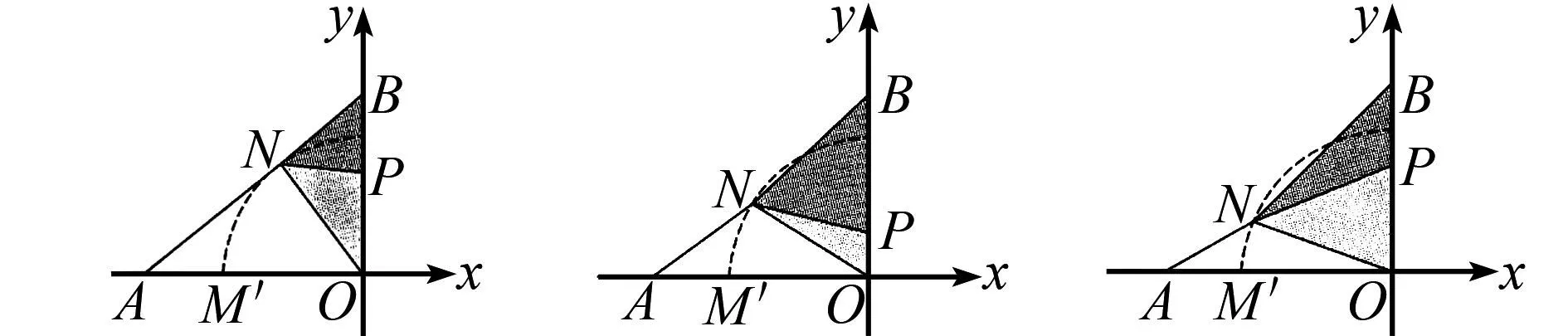
图4 探究定值问题

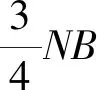
2.4 解法探究

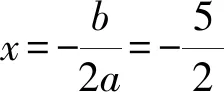
(2)解法1 如图5所示,EM⊥x轴,M(m,0),则

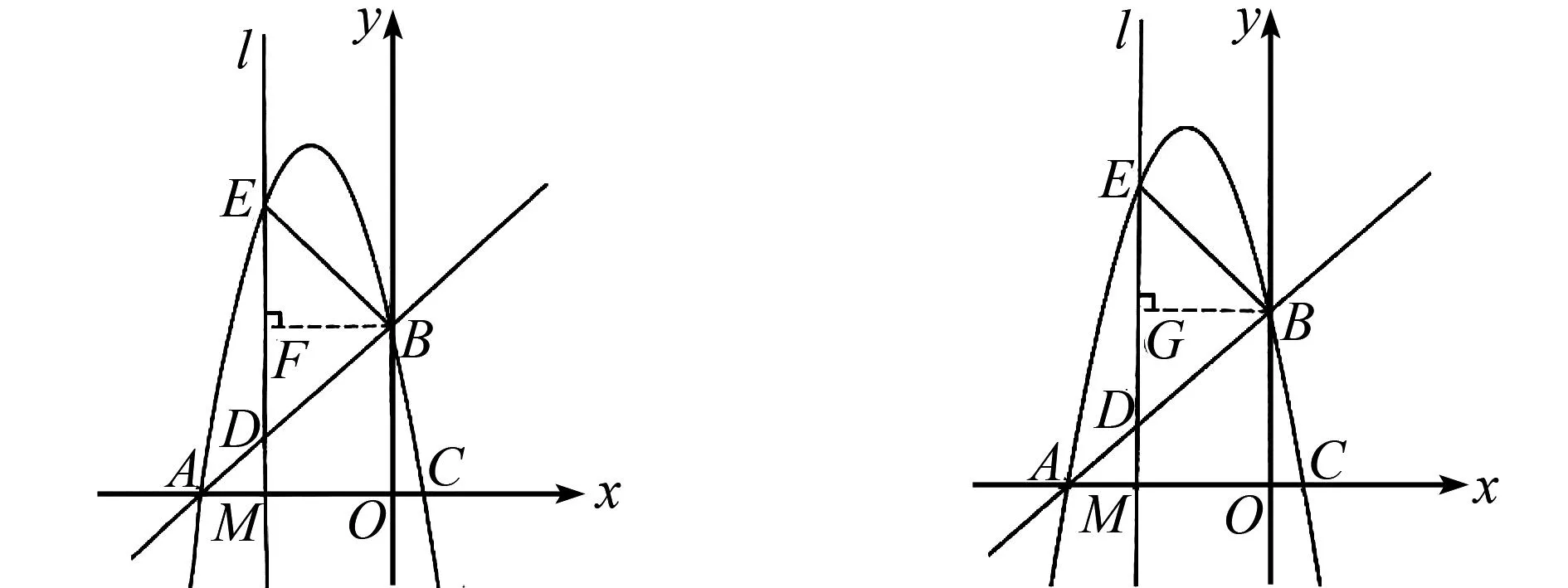
图5 解法1图

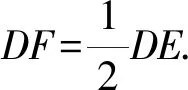
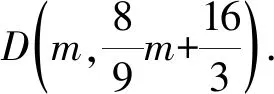
当DE为底时, 作BG⊥DE于G,则

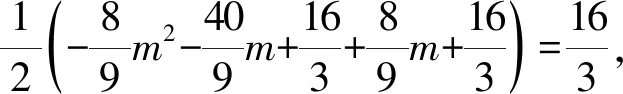
解得m1=-4,m2=0(不合题意,舍去).

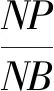
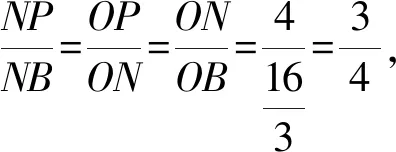
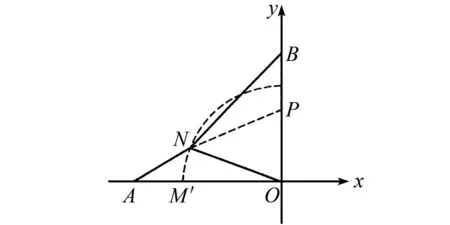
图7 第(3)问图

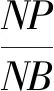
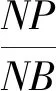
3 结束语

探求定值一般是先分清问题的不变量与变量,而定值往往与这些不变量中的某些量(或它们的代数式)有关,常将一般问题特殊化,运用特殊情形(即用特殊值、特殊位置、特殊图形等)探求定值.