基于Polyak步长的随机递归梯度算法

王福胜,李晓桐

(太原师范学院数学与统计学院,山西 晋中 030619)

1.引言

在机器学习中,经常会出现以下的优化问题:

其中n是训练集大小,每个fi,i ∈{1,2,···,n}是凸函数且有Lipschitz连续导数.解决上述优化问题的标准有效的方法为梯度下降法(GD)[1].对于光滑优化问题(1.1),梯度下降的迭代方法为

其中ηt>0表示步长.当n较大时需要计算全梯度,导致计算量很大.Robbins和Monro[2]在1951年提出了随机近似(stochastic approximation,SA).之后,研究者提出了随机梯度下降(stochastic gradient descent,SGD)[3-4],该方法的迭代公式如下:

其中下标it是从{1,2,···,n}中随机选取得到.

在机器学习中有一系列改进SGD的工作[3-4].SGD算法的收敛性质取决于随机方向和真实梯度的方差,因此,如何缩减方差是改进SGD的方法之一.常见的有随机方差缩减梯度算法(SVRG)[5],随机递归梯度算法(SARAH)[6],随机平均梯度算法(SAG)[7]等.

对于方差缩减类算法而言,步长也是关键因素.传统的步长要选择递减步长或者较小的固定步长,并且满足

关于步长的工作也有很多,AdaGrad[8]和Adam[9]等采用对角修正技术为每个分量自适应地选取步长.当前,由于BB步长[10]特有的性质,许多学者将方差缩减方法与BB步长相结合,如SARAH-I-BB[11]算法.本文考虑将Polyak[12]步长与随机递归梯度下降算法[6]结合,提出SARAH-Polyak.

2.算法

其中,it ∈{1,2,···,n}.可以看出,SARAH算法的迭代方向vt是真实梯度的有偏估计,即

接下来,我们介绍一下Polyak[12]步长,它普遍用于投影次梯度法.假设我们要求解以下的无约束优化问题:

其中f:Rd →R是凸但可能非光滑的函数.假设f在xk处的次梯度f′(xk)∈∂f(xk)是可计算的.投影次梯度法有如下形式:

再根据文[13]中引理8.11有

其中x∗是问题(2,1)的最优解,f(x∗)是(2.1)的最优值.tk的一种选择是取不等式(2.2)右端的最小值,因此有

当f′(xk)=0时,上述式子未定义,我们可以人为的定义tk=1(也可以取任意正数),最后得到Polyak步长

从上述表达式可知,Polyak步长依赖于f(x∗)的值.在一些应用中,f(x∗)的值是已知的.并且现有的算法中Polyak步长使用的是随机的次梯度,而本文使用的是全梯度.即

文[14]构建了一个简单函数h,通过下式计算步长

函数h有不同的形式:

因为在早期迭代中,可以选取较大步长加速收敛,然后逐渐选择较小步长防止振荡.因此,当选取h=g(k)时,可以令g(k)是关于外循环数k的单调递增函数.文[14] 中的算法(SARAH-AS)选取函数的具体形式如下:

为了加快收敛,本文中的步长也采用上述方式,具体形式为

其中tk为(2.4)中的步长,h=

下面我们将上述Polyak步长与随机递归梯度下降算法相结合构造成新的算法,算法框架见算法2.

3.收敛性分析

假设3.1假设每个函数fi(x)都是凸函数,且目标函数F(x)是µ-强凸的,即

这里我们定义x∗为问题(1.1)的最优解.并且由于F(x)是强凸的,因此x∗是唯一的.

假设3.2假设每个函数fi(x)的梯度是L-Lipschitz连续的,即

即∇F(x)也是L-Lipschitz连续的.

引理3.1[15]假设F(x)是凸函数,且∇F(x)是L-Lipschitz连续的,则对∀x,y ∈Rd,有

引理3.2[15]假设F(x)是凸函数,且∇F(x)是L-Lipschitz连续的,则对∀x,y ∈Rd,有

上面最后一个不等式中我们利用了引理3.6以及F(x)的强凸性.并且有

即算法2具有R-线性收敛速度.

证根据目标函数F(x)的强凸性以及∇F(x∗)=0,可知

上式蕴含算法2具有R-线性收敛速度.

近年来,强凸性假设一直是证明算法收敛的标准假设,但这一假设并不适用于文献中的许多问题.为了在一般凸条件下证明算法的收敛性,我们先给出一些条件.我们将X∗表示为问题(1.1)的最优解集,将xproj表示为x在X∗上的投影.因此,∇F(xproj)=0.我们使用x∗表示(1.1)的最优值.首先假设F是一阶连续可微的,并且F是L-Lipschitz连续的,ν>0.我们给出以下四个条件:

接下来,我们分析了RSI条件下SARAH的性质.

引理3.7[11]若假设F是凸的并且满足(3.1)并且∇F(x)是L-Lipschitz连续的,那么对于任何α ∈[0,1],有

4.数值实验

在本节中,通过数值实验结果验证算法SARAH-Polyak的有效性.我们针对机器学习中二分类的ℓ2正则化逻辑回归问题: 给定一组训练集(a1,b1),(a2,b2),···,(an,bn),其中ai ∈Rd,bi ∈{+1,-1},通过求解下列问题得到最优预测值x ∈Rd,

其中λ>0是正则化参数.我们使用了三个公开的数据集,数据集的大小为n,维度为d,详细信息如表4.1所示,所有数据可以在LIBSVM网站(www.csie.ntu.edu.tw/∼cjlin/libsvmtools/datasets/)下载.表中还列出了实验中所选取的λ>0值(在所有数据集上设置参数为λ=10-4,m=2n.所有的数值实验均在相同的Python计算环境下进行.所有的实验结果如图4.1-4.6所示.

图4.1 heart上的残差损失

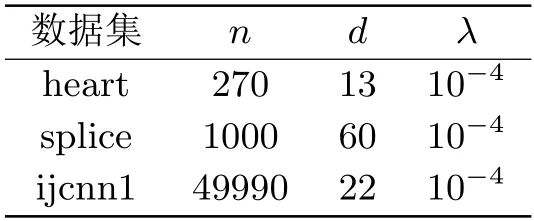
表4.1 数值实验中使用的数据集和正则化参数

图4.1到图4.6展示了SARAH-BB,SARAH 以及SARAH-Polyak三个算法在数据集heart,splice和ijcnn1上的残差损失及步长变化趋势.在所有的图中,蓝色,红色和绿色实线代表不同步长的SARAH-Polyak 算法;黑色实线代表最优步长的SARAH-BB算法;蓝色,红色和绿色虚线对应着固定步长的SARAH算法.在所有的图中,x轴代表外循环数,图4.1,4.3和图4.5中y轴表示最优间隔，即F(xk)-F(x∗),图4.2,4.4和4.6中y轴表示步长变化趋势.

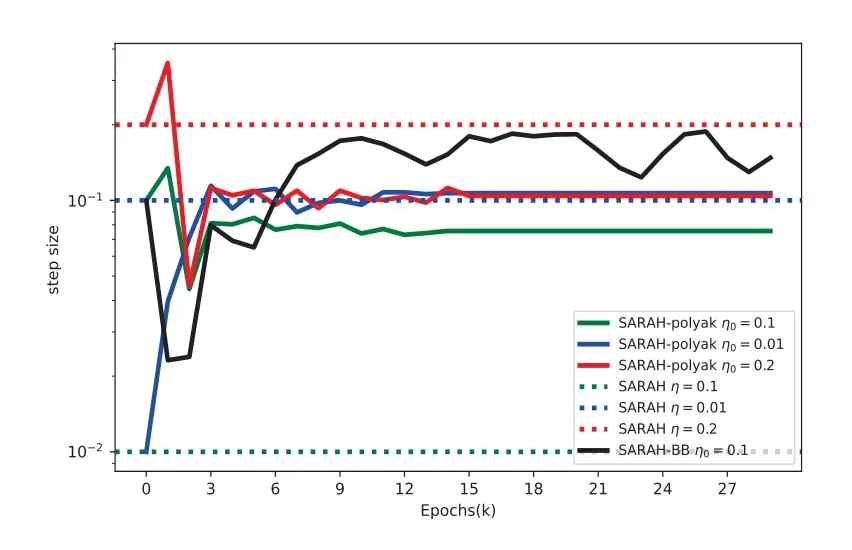
图4.2 heart上的步长变化趋势

图4.3 splice上的残差损失

图4.4 splice上的步长变化趋势

图4.5 ijcnn1上的残差损失

图4.6 ijcnn1上的步长变化趋势

从图4.1,4.3和4.5中可以看出:SARAH-Polyak算法收敛速度整体上比采用固定步长的SARAH 算法快,并且当选择不同的初始步长η0时,SARAH-Polyak算法的收敛性能不受影响.并且SARAH-Polyak与最优步长的SARAH-BB算法相差不大.图4.2,4.4和4.6中可以看出: 当选取不同的初始步长时,SARAH-Polyak算法的步长最终收敛于最优步长的邻域.

5.结论

在本文中,我们提出了一种改进的算法SARAH-Polyak.首先我们用理论说明Polyak步长并没有增加算法的复杂度,因为该算法已经计算出全梯度,并且可以通过其他算法得到最优值.然后分别在强凸和一般凸的假设下证明了它的收敛性.最后从实验结果分析来看,相比于使用固定步长的SARAH算法,新算法的收敛速度更快,并且可以和最优步长的SARAH-BB相媲美,不受初始步长选取的影响.新算法对初始步长的选择是有效的.