解析交点圆系方程的几何意义——读《两圆无交点，圆系为何意》有感

●

(中山纪念中学 广东中山 528454)

解析交点圆系方程的几何意义
——读《两圆无交点，圆系为何意》有感

●姚华鹏

(中山纪念中学 广东中山 528454)

笔者阅读了文献[1]后，对作者的研究精神深表敬意.不过,笔者认为文中给出的结论似乎有些牵强，以至于作者自己也承认结论没有实际意义.因此,笔者对“两圆相离、内含时,圆系方程没有实际意义”的说法心存疑虑.很多中学数学竞赛资料提到交点圆系方程，但是均未能给出交点圆系方程的由来.对此笔者近期思索了一些相关问题，特撰文与大家商榷，以期通过定义距径平方差揭开圆系方程的面纱.

若圆C的方程为x2+y2+Dx+Ey+F=0(D2+E2-4Fgt;0),配方后成为标准方程,即

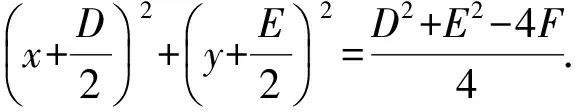
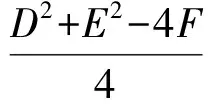
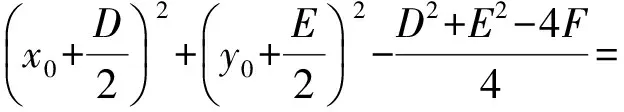
因此

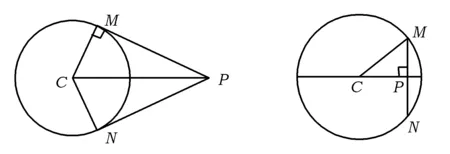
图1 图2

当点P在圆内时，如图2所示，过点P引线段PC的垂线，交圆C于点M，N(此时,弦MN是圆内过点P的最短弦).由垂径定理知

|PM|2=MC2-PC2=R2-PC2,

从而

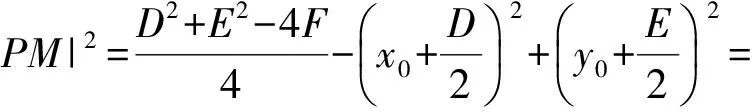
于是

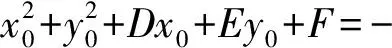
当定点P在圆上时，亦有

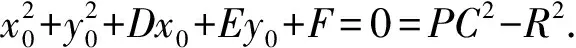
到圆C1:x2+y2+D1x+E1y+F1=0(半径为r1)与圆C2:x2+y2+D2x+E2y+F2=0(半径为r2)的距径平方差之比为-λ的点S(x,y)的轨迹方程为

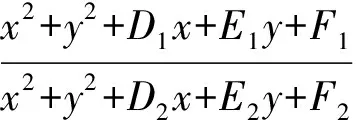
(1)

无论实数λ为何值，式(1)变形整理得

x2+y2+D1x+E1y+F1+λ(x2+y2+E2x+

E2y+F2)=0，

(2)

即为熟悉的交点圆系方程.交点圆系方程的几何意义自然而出：表示到两圆的距径平方差之比为-λ的点的轨迹方程！

下面我们证明:方程(2)一定是某个圆的方程.

当λ≠-1时，方程(2)可化为

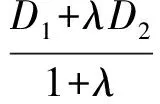
要证明该方程表示圆,则只需证明

(把点看成半径为0的圆)即可.此不等式不易得证,而它实际上是要证明方程(2)有解.如果能够证明存在满足方程(1)的点，那么即证明了该不等式成立.考虑到对于任意的点S，有

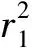
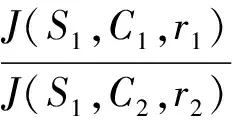
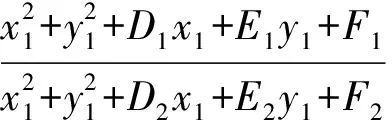
由此可知方程(1)有解，从而方程(2)有解.因此方程(2)确实是某个圆的方程！把直线看成半径无限大的圆，则当λ=-1时，方程(2)也表示是圆.当圆C1与圆C2有公共点时，方程(2)所表示的圆过它们的公共点.即使圆C1与圆C2相离或内含,方程(2)仍然能够保持其本质意义.故把方程(2)称为交点圆系方程是比较片面的！

用方程(1)能够轻松解释下列现象：

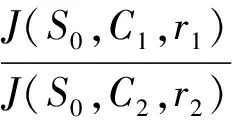
J(S0,C1,r1)=J(S0,C2,r2).

当点S0(x0,y0)落在两圆外时，由它引两圆的切线长相等.这是很多参考资料都有的结论.其实,对于λ≠-1的方程(2)对应的曲线上的点亦可类似地讨论切线长的关系，方程(1)正好给出了它们之间的关系.

(2)由于方程(1)的分母不能为0，因此满足方程(2)的解对应的点不能落在圆C2上，自然圆C2的方程无法用方程(2)表示.当λ=0时,方程(2)表示的曲线显然是圆C1；若把方程(2)改写成

λ1(x2+y2+D1x+E1y+F1)+λ2(x2+y2+

D2x+E2y+F2)=0,

则当λ2=0，λ1≠0时,就能够表示圆C2.

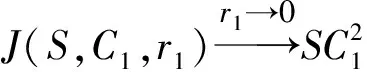
因此到两定点的距离之比为定值(正数)的点的轨迹是圆，这可以作为圆的第二定义.

[1] 刘薇，陆丽滨.两圆无交点，圆系为何意——记一次对虚圆系的探究过程[J].中学教研(数学)，2010(1):1-2.