改变教学方式，提高学生质疑能力

☉江苏海门市东洲中学 徐 新

改变教学方式，提高学生质疑能力

☉江苏海门市东洲中学 徐 新

质：质问、询问、提问.疑：疑惑、疑问、问题.质疑能力：发现问题和提出问题的能力.而在数学教学中更是指学生的一种反思能力，是学生思维的激发和提升.通过质疑能力的提升，形成良好的逻辑思维能力.

在大力发展素质教育的现在，我们一线教师常常发现初一学生课堂气氛活跃，举手率较高，到初二愿意自主举手的学生逐渐少了，而到了初三甚至整堂课没有一个学生举手提问，这是什么原因呢？我想除了学生的生理、心理从初一到初三发生了变化以外，产生这一现象的真正原因可能是我们教师长期采用传统的教学方法.学生习惯于“听”教师在课堂的“讲”，而自己却不加思考，久而久之，质疑能力就大大降低，培养的学生只会做题，不会思考，依赖性强，创造力差.所以要改变这一状况，我认为一定要改变传统的教学方式，再也不能采用象“填鸭式”“灌输式”这种被动的教学方式，而应变为“开放式”“民主式”“互动式”的教学方式.事实上现在教师已经在改变了.

一、启惑——为学生创造质疑的机会

传统的教学方式，是以教师为中心，课堂上教师只注重向学生进行知识的传授，教师讲学生听，学生处于被动识记的状态中，没有自主性和主动性，课堂有的是呆板重复的训练，不能调动学生的学习兴趣，无形中抑制了学生的发问，抑制了学生的思维发展，阻碍了学生质疑能力的提高，创新思维变成了一句空话.改变这一切，必须从教师这一头做起，改变教学方式.

洋思中学的“先学后教，当堂训练”的教学模式值得我们学习和借鉴.教师不再是中心，教师的责任不在于教，而在于指导学生的学.“先学后教，以教导学，以学促教.”使学生在学习的基础上产生疑惑.学生与学生互动式学习，大大提供了质疑的机会，而学生与学生之间处于一种平等的状态，相互之间没有顾虑，这样学习的积极性高了，课堂气氛活跃了.

还有，我们海门市教育局在全市范围推行的“学程导航”教学模式，它的第一个环节是预习，预习作业——课前；预习展示——课始.通过学生预习中存在的问题和已自主获得的认识的不断展示，教师引导学生试探着运用方法得出新知.学生在做预习作业时一定有所疑惑，会在课堂上呈现出来，从而产生思维的碰撞.我认为它把我们课堂上部分学生的思维或质疑提前到课前的自学中，然后在课堂中释疑.特别对那些思维速度一般的学生而言（这部分学生占全班的大多数），有了充足的准备时间，为课堂教学做好充分的铺垫，从而使课堂教学显得紧凑而高效.例如，在《有理数》一课中，就有学生提出如下的一些问题：①在把下列各数填入它所属于的集合的圈内，为什么要有省略号？②象温度计、海拔高度等抽象出的“直观方式”——数轴，可不可以竖直画？（因为书上的数轴都是画成水平的）③由绝对值的定义可知：当a是负数时，｜a｜=-a.可看着“-a”明显有“-”号，这是为什么？等等.这些问题既有一定的深度，又确实是学生不太明白有疑惑的，教学时，“以学定教”、“顺学而导”，立足学生自学中存在的问题、自学后的起点实施教学，不讲学生已经会的、不讲学生通过自学也能会的，只针对学生不理解的（由学生提出来）给学生充分的质疑的机会，课堂上师生共同解决学生的疑难问题.问题让学生自己去揭示，知识让学生自己探索，规律让学生自己去发现，学法让学生自己去归纳，效果让学生自己去评价.只有学生实在解决不了的问题，老师再作出点拨，适当讲解.这一理念是完全符合学生的认知规律的.

二、和谐——为学生营造质疑的氛围

民主和谐的教学氛围是学生积极性、主动性发挥的前提.它能消除学生的紧张心理，能使学生在一种较为宽松的环境中学习.教师要改变传统的地位观念，俯下身子与学生交流，增强与学生的亲近度，缩短与学生身心的距离，这样才能让学生人格上独立，思想上自由，学生也才能大胆探索，主动提问.

南通市李庾南老师的“自学、议论、引导”教学法值得我们学习和借鉴.她的方法是根据青少年学生的好奇心、求知欲、表现欲，结合课堂教学内容，给学生营造民主和谐的学习氛围.特别是“议论”这一环节，能充分培养学生的质疑能力，让学生好疑好问的天性得到发挥，让主动质疑的学生能激发、带动更多的学生积极思考，进而提高课堂教学效果.

同样，山东杜郎口的“三、三、六”自主学习教学模式，在培养学生质疑、营造课堂质疑氛围上也值得我们学习和借鉴.他们对课堂学习评价的标准是“举手积极，声音洪亮，辩论热烈，争问抢答，欢呼雀跃，多种角度，创新实践，笑逐颜开，热闹非凡”“敢问、敢说、敢爬黑板、敢下桌讨论”等等；有了这样的课堂标准，就有了滋润学生质疑的温床，这样开展素质教育就不会是一句口号.

当然，我们每位教育工作者都知道，教学有法而无定法，我们一定要针对学生的实际情况，针对不同的教学内容，选择、使用恰当的、适合学生的教学方式，为学生营造良好的质疑氛围.

三、抛砖——培养学生质疑的好品质

改变教学方式，最重要的是改变目前教师教的方式，只有改变教师教的方式，才能改变学生传统的学习方式，也才能适应当前素质教育的新要求.提高学生的质疑能力，不是教师在课堂上多问几个“为什么”就能轻易做到的，除在课堂上多提供质疑的机会，营造学生提问的氛围上多下功夫，还应在指导学生质疑的方法上和如何面对学生质疑上多有备案.

下面结合初中数学教学实例片段，谈谈如何培养学生质疑的好品质.

在讲解《勾股定理》的证明时，首先按照学生自学的投影展示书中的证明（见下图）：

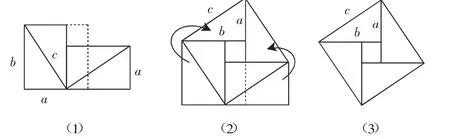
接着提出一个简单的问题（预习中的），同学们对课本的证明还有什么想法？你能有不同的解吗？

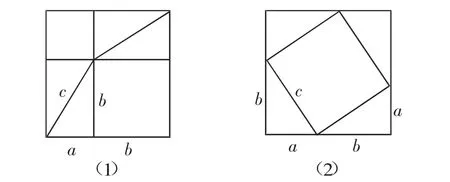
可能一：

对照图（1）和（2）两个大正方形大小一样，都包含4个相同的直角三角形，所以得：a2+b2=c2.

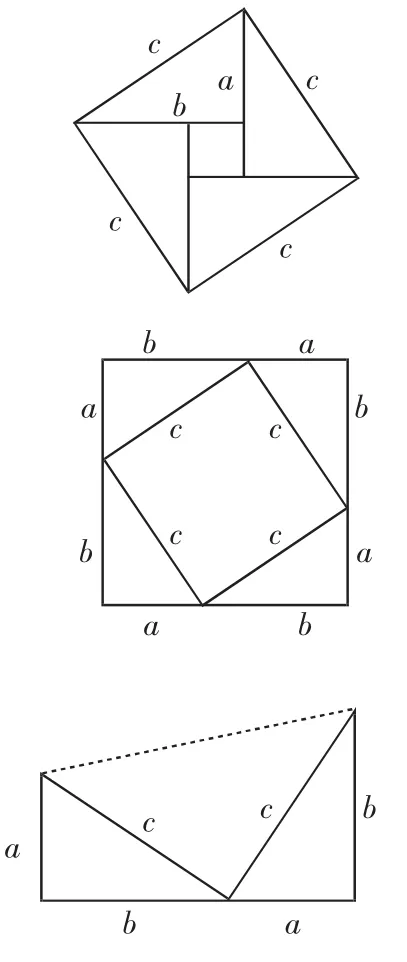
可能二：

可能三：

可能四：

……

因为现在学生很多时候都会囿于现成的知识和方法，而不思创新（即通常的惰性），这就要求教师通过不同的方法，激发学生的思维.象上例，根据学生和课堂情况，展示上面其中的一种方法，因为学生的一切活动往往是从模仿开始，这样可起到抛砖引玉的作用，启动学生思维的内驱力，激发他们的求知欲，引导学生寻

找不同的方法解决问题，培养学生的思维能力和品质.

到此也许有学生就会发问，上面的方法都是实验操作及面积计算，有没有其他不同的几何证明？我会因势利导：

可能五：

本方法又回到引例中，易证△ABE≅△FBC，通过全等形面积相等，得它们的面积相等，从而正方形BCDE和正方形BFLH的面积相等.同理正方形ACNM和正方形AGLH的面积相等，所以正方形BCDE和正方形ACNM的面积之和等于正方形ABFG的面积，即有a2+b2=c2.

可能六：

以正方形ABFG的边FG为边向形外作三角形FGH和三角形ABC全等，连接DN、ECM、CH，易证4个四边形全等，它们是四边形DEMN、四边形BEMA、四边形BCHF、四边形ACHG，通过观察比较得正方形BCDE和正方形ACNM的面积之和等于正方形ABFG的面积，即有a2+b2=c2.

可能七：

由比或相似或三角函数或射影定理：a2=BD×BA，b2=AD×BA，所以a2+b2=BD×BA+AD×BA=BA2=c2，即有a2+b2=c2.

……

告诉学生勾股定理的证明有几百种之多，把课堂知识延伸到课外，也就把质疑品质的培养贯穿于课内外.

有了勾股定理的证明的教学铺垫，下面的勾股定理的应用也就水到渠成.

要培养学生的质疑能力，教师教学中要精心准备教案，要做有心人，要让学生想问，敢问，好问，更应让学生会问.当然这不是一朝一夕就能解决的事情，需要教师长久的，持之以恒地研究教材，研究学生，改变教学方式，比如每堂课要精心准备预习作业，设计巧妙的提问方式，关注学生全面发展，在教师的潜移默化的影响下，学生的质疑能力才能得到提升.

总之，在实施素质教育的今天，要提高学生的质疑能力，应在课堂上通过多种形式和方法，为学生创造质疑的机会——想问，为学生创造质疑的氛围——敢问，培养学生质疑的品质——好问，会问.只有这样，才能使学生逐步由被动质疑向主动质疑转变，让学生充满信心和提高学习兴趣，从而能调动学生学习的积极性，使学生各方面的能力得到发展，也为学生可持续发展打下坚实的基础.