高中数学中思想方法的应用——高中数学中的函数与方程思想

陈燕青（江苏省盱眙中学）

高中数学中思想方法的应用
——高中数学中的函数与方程思想

陈燕青
（江苏省盱眙中学）

函数属于高中数学中的重要概念与思想，而且它所包含的内容也相当广泛，其概念与思想渗透到高中数学的各个部分，所以函数思想对高中生的数学学习具有重要的意义与作用.因此，主要针对此，对函数与方程思想在高中数学教学中的运用进行分析，借助案例分析的形式，研究函数思想的合理运用，并为高中的数学教育做出一定的贡献，希望能够促进高中数学教学的积极发展.

高中数学；函数与方程思想；直线

认知主义学习理论将数学看成是对知识、规律逐渐发现与理解的过程，这就要求学习者在数学学习中不断摸索，了解数学的精神，掌握其思想方法，尤其是与生活息息相关的函数与方程思想.建构主义认为，知识是主动建构的，不是被动接受的，知识在每个学习者头脑中都不是客观存在的，而是由每个学习者主动参与认识活动而主观创造出来的.

一、函数与方程思想在导数中的应用

导数在近几年的高考中占据重要地位，而构造函数与方程思想在导数中的应用是各级、各类考试中的热点问题.导数的单调性、极值、最值等性质的研究常常和函数与方程思想相结合，主要综合考查学生的思维能力.

例1（2014南通三模）已知函数f（x）=（x-a）2ex在x=2时取得极小值.

（1）求实数a的值；

（2）是否存在区间［m，n］，使得f（x）在该区间上的值域为［e4m，e4n］？若存在，求出m，n的值；若不存在，说明理由.

解：a=2，过程略.

（2）因为f（x）≥0，所以m≥0.

①若m=0，则x≥2，因为f（0）=4＜e4n，所以（n-2）2en=e4n.

所以g（x）在［2，+∞］上为增函数.

由于g（4）=e4，即方程（n-2）2en=e4n有唯一解为n=4.

②若m＞0，则2∈［m，n］，即n＞m＞2或0＜m＜n＜2.

由①可知不存在满足条件的m，n.

设h（x）=x（x-2）2ex（0＜x＜2），则h＇（x）=（x3-x2-4x+4）ex=（x+2）（x-1）（x-2）ex.

h（x）在（0，1）上递增，在（1，2）上递减，由h（m）=h（n）得0＜m＜1，1＜n＜2，此时（m-2）2em＜4e＜e4n，矛盾.

综上所述，满足条件的m，n值只有一组，且m=0，n=4.

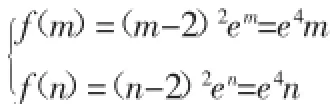
二、函数与方程思想在解析几何中的应用

在解析几何的相关问题中，若遇到直线和圆、直线和圆锥曲线的位置关系，常常会联立方程组研究，而遇到解析几何中的最值问题时常常会用函数去研究.

例2（2015年全国高中数学联赛江苏赛区）如图1，在平面直角坐标系xoy中，圆O1，圆O2都与直线l∶y=kx及x轴正半轴相切.若两圆的半径之积为2，两圆的一个交点为P（2，2），求直线l的方程.

解：由题意，圆心O1，O2都在x轴与直线l的角平分线上.

若直线l的斜率k=tanα，

圆心O1，O2在直线y= tx上，

可设O1（m，mt），O2（n，nt）.

交点P（2，2）在第一象限，m，n，t＞0.

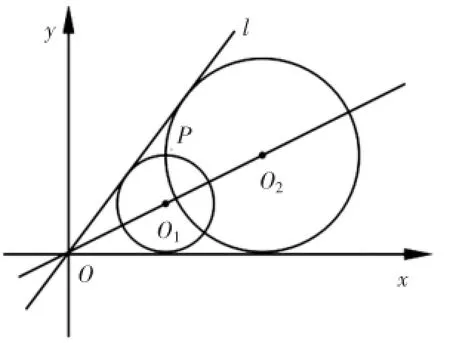
图1　

所以，O1∶（x-m）2+（y-mt）2=（mt）2，O2∶（x-n）2+（y-nt）2=（nt）2，

所以m，n是方程x2-（4+4t）x+8=0的两根，mn=8.

点评：这道题考查了直线的方程、圆的方程等知识，考查了方程思想的应用.由直线l的方程，可以引进参数t，建立的直线O1O2的方程.再根据过点P（2，2）建立方程组，渗透了方程组的思想，但是在整个问题的解决过程中自始至终都渗透了建立关于参数t的方程的思想.

希尔伯特说过：数学学科是一个不可分割的有机整体，它的生命力正在于各个部分之间的联系.函数与方程思想固然重要，但是也离不开与其他思想方法的联系，要想学好数学，攻克解题难关就必须掌握好各种基本知识、方法、思想之间的联系.学生在解题过程中，认真分析各个条件及各个条件之间的联系，尝试用数学思想方法找到解题方向.所以仅仅教会学生知识和方法是远远不够的，没有思想方法的提炼和融会贯通是走不远的，函数与方程思想是高考考查的重点和难点，教师在平常的教学过程中，要不断地渗透给学生，还要注意和各种思想方法综合使用.

三、函数在数列问题中的应用

四、函数与方程思想在不等式中的应用

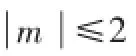
五、函数与方程思想在实际问题中的应用

例如，有这样的实际问题：某班的20名同学在直线公路上栽树，每人植一棵，而且相邻两棵树的距离为10米。在开始过程中，需要把树苗集中放在某一个树坑旁边，能够让每位同学领取树苗所用的路程总和最小，求这个最小值。对于这一问题来说，应该建立合适的数学模型，通过列式向函数的最值问题转化。如图2所示。

图2　

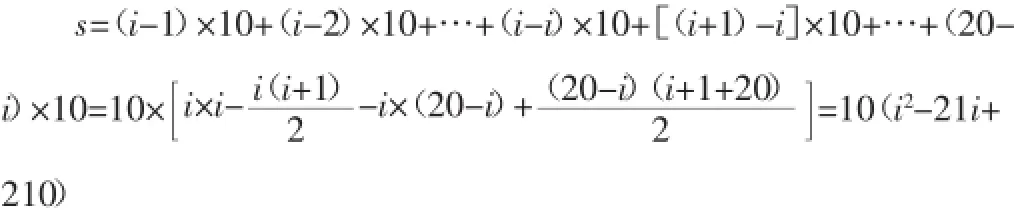
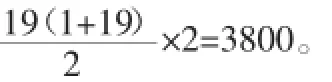
总之，作为高中数学基础知识的重要内容，数学思想与数学方法属于教学中的重点，也是学生在学习过程中的难点。通过数学思想与方法的学习能够真正理解数学的价值与意义。高中数学的学习离不开函数的思想与作用，函数的学习能够为其他知识的掌握奠定一定的基础，而且函数思想也属于数学学习中的重要指导思想。因此，本课题针对函数与方程思想，对其在高中数学教学中的运用进行研究，主要是关于解决数学问题的案例分析，以此能够为高中数学教学提供合理的借鉴，促进高中生数学的学习与进步。

·编辑李琴芳