导数背景下的函数对称性探究

陕西省西安惠安中学 (710302) 龙正祥

利用导数研究函数的单调性，解决函数的极值、 最值、零点等问题成为当下高考关注的热点，关于导数与函数单调性的研究颇深.但利用导数研究函数的对称性的案例较少，导致在解决函数对称性时很少考虑导数这条解题思路.本文通过梳理函数自对称结论的基础上，研究导函数与原函数的对称性关系及应用，希望能给读者在解决这类问题时提供一点启示.

1 函数自对称结论的梳理

定理1 函数y=f(x)的图像关于直线x=a对称的充要条件是对定义域内的每一个x恒有f(a-x)=f(a+x)成立.

证明：(充分性)若f(a-x)=f(a+x)对定义域内的每一个x恒成立，设点P(x,f(x))是y=f(x)图像上任意一点，则它关于直线x=a的对称点Q坐标为 (2a-x,f(x))，∴f(2a-x)=f[a+(a-x)]=f[a-(a-x)]=f(x)，∴点Q(2a-x,f(x))的坐标满足方程y=f(x)，即点Q(2a-x,f(x))也在函数y=f(x)的图像上，∴函数y=f(x)的图像关于直线x=a对称.

(必要性)若函数y=f(x)的图像关于直线x=a对称，设M(x,y)是函数y=f(x)的图像上的任意一点，则y=f(x)的图像上点M(x,y)关于直线x=a的对称点为N(2a-x,y)，∵y=f(x)的图像上关于直线x=a对称，点N在y=f(x)的图像上，∴f(2a-x)=y， ∴f(2a-x)=f(x).∴f(a-x)=f(2a-(a+x))=f(a+x).

推论1.1 函数y=f(x)的图像关于直线x=0(y轴)对称(偶函数)的充要条件是对定义域内的每一个x恒有f(-x)=f(x)成立.

推论1.2 函数y=f(x)的图像关于直线x=a对称的充要条件是对定义域内的每一个x恒有f(2a-x)=f(x)成立.

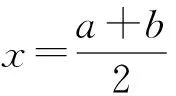
定理2 函数y=f(x)的图像关于点(a,b)对称的充要条件是对定义域内的每一个x恒有f(a-x)+f(a+x)=2b成立.

证明：(充分性)若f(a-x)+f(a+x)=2b对定义域内的每一个x恒成立，设点P(x,f(x))是y=f(x)图像上任意一点，则它关于点(a,b)的对称点Q坐标为 (2a-x,2b-f(x))，∴f(2a-x)=f[a+(a-x)]=2b-f[a-(a-x)]=2b-f(x)，∴点Q(2a-x,2b-f(x))也在函数y=f(x)的图象上，∴函数y=f(x)的图像关于点(a,b)对称.

(必要性)若函数y=f(x)的图像关于点(a,b)对称，设M(x,y)是函数y=f(x)的图像上的任意一点，则y=f(x)的图像上点M(x,y)关于点(a,b)的对称点为N(2a-x,2b-y).∵y=f(x)的图像上关于点(a,b)对称，且点N在y=f(x)的图像上，∴f(2a-x)=2b-y， ∴f(2a-x)=2b-f(x)，∴f(a-x)=f(2a-(a+x))=2b-f(a+x)，∴f(a-x)+f(a+x)=2b.

推论2.1 函数y=f(x)的图像关于点(0,0)(原点)对称(奇函数)的充要条件是对定义域内的每一个x恒有f(-x)+f(x)=0成立.

推论2.2 函数y=f(x)的图像关于点(a,b)对称的充要条件是对定义域内的每一个x恒有f(2a-x)+f(x)=2b成立.

2 两个函数对称性的关系

定理3 记定义在R上的可导函数f(x)的导函数为f′(x),则函数y=f(x)的图象关于点(a,f(a))对称的充要条件是导函数f′(x)的图像关于直线x=a对称.

证明：(充分性)若f′(x)的图像关于直线x=a对称，则由推论1.2得f′(2a-x)=f′(x)，从而有

(必要性)若函数y=f(x)的图像关于点(a,f(a))对称，则由推论2.2得f(x)+f(2a-x)=2f(a)，从而两边求导可得f′(x)-f′(2a-x)=0，即f′(x)=f′(2a-x).故由推论1.2得函数f′(x)的图像关于直线x=a对称.

推论3 若函数f(x)为可导的奇函数，则其导函数f′(x)为偶函数.

定理4 记定义在R上的可导函数f(x)的导函数为f′(x),则函数y=f(x)的图像关于直线x=a对称的充要条件是导函数f′(x)的图像关于点(a,0)对称.

(必要性)若函数y=f(x)的图象关于直线x=a对称，则由推论1.2得f(x)=f(2a-x)，从而两边求导可得f′(x)=-f′(2a-x)，即f′(x)+f′(2a-x)=0.故由推论2.2得函数f′(x)的图像关于点(a,0)对称.

推论4.1 若函数f(x)为可导的偶函数，则其导函数f′(x)为奇函数.

推论4.2 记定义在R上的可导函数f(x)的导函数为f′(x)，若函数f(x)图像关于直线x=a对称，则必有f′(a)=0.

3.实例分析

思路1：利用定理1，建立恒等式，从而得到实数a的值.

施工承建单位的项目经理是项目建设质量、进度和投资控制的关键。一个具有较丰富施工管理经验和质量意识、敬业精神、责任心都强的项目经理，在承担中标工程项目任务时，都会挑选自己信任的得力助手，包括主管生产的副经理、总工、质检负责人等。这样的经理进场后，以他为核心的项目组会结合工程施工实际制定施工措施和质量管理办法等，并且能落到实处，保障工程施工建设得以顺利进行。

思路2：利用推论4.2，通过求导函数，而得到实数a的值.

点评：思路1利用传统方法(定理1)，建立恒等式，通过三角恒等变换，得到实数a的值，思路2利用导函数与原函数对称性的关系，问题很容易得到了解决，这就是“横看成岭侧成峰，远近高低各不同”的数学文化，这就是“润物细无声”的数学抽象素养和数学运算素养的培养.

例2 求函数f(x)=ax3+bx2+cx+d(a≠0)图像的对称中心.

思路1：利用待定系数法，通过定理2建立恒等式来解决.

解法1：设对称中心为点(m,n),由f(m-x)+f(m+x)=2n,得a(m-x)3+b(m-x)2+c(m-x)+d+a(m-x)3+b(m-x)2+c(m-x)+d=2n,化简得(3am+b)x2+am3+bm2+cm+d=n,要使上式恒成立，

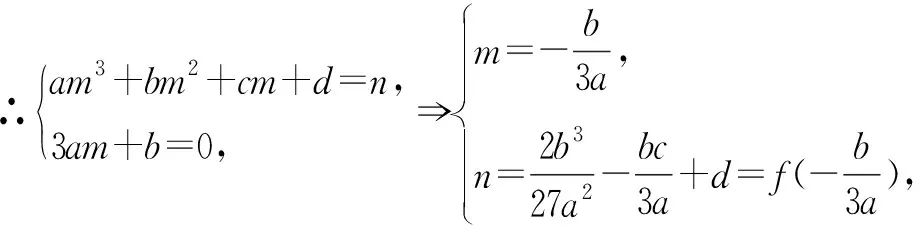
思路2：利用定理3，通过探求导函数的对称性，解决原函数的对称性.

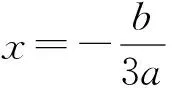
点评：思路1利用传统方法(定理2)，建立恒等式，通过多项式的运算和化简，得到了对称中心，思路2利用导函数与原函数对称性的关系，将三次函数的对存在性问题转化成了二次函数的对称轴问题，这就是“柳暗花明又一村”的数学文化，这就是数学抽象素养(导数)“四两拨千斤”的价值体现,这就是逻辑推理素养与“无形之有形”中的培养.

4.考题链接

题1 (2017年Ⅱ卷文第13题)函数f(x)=2cosx+sinx的最大值.

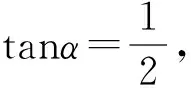
题2 (2018年Ⅰ卷文第6题) 已知函数f(x)=x3+(a-1)x2+ax.若f(x)为奇函数，则曲线y=f(x)在点(0,0)处的切线方程为( ).

A.y=-2xB.y=-xC.y=2xD.y=x

解析：由推论3知，二次函数f′(x)=3x2+2(a-1)x+a为偶函数，从而得a=1，此时f(x)=x3+x，f′(x)=3x2+1，k=1，所以曲线y=f(x)在点(0,0)处的切线方程为y=x，故选D.