双直线二次曲线法求直线

安徽省怀宁县新安中学(246121) 张国节

在圆锥曲线问题当中,经常会出现两条直线与圆锥曲线有四个交点的情况,本文通过将这两条直线写成双直线二次曲线的形式,来求出经过其中两点的直线,进而解决一些定点、定值问题.

1 问题初探

例1(2020 全 国1 理20) 已知A, B 分别为椭圆= 1(a > 1)的左、右顶点, G 为E 的上顶点,= 8,P 为直线x = 6 上的动点,PA 与E 的另一交点为C,PB 与E 的另一交点为D.

(1)求E 的方程.

(2)证明: 直线CD 过定点.

解(1)E 的方程:=1.

(2) 如图1, 设P(6,y0), 则lAP: 9y -y0x-3y0= 0,lBP:3y-y0x+3y0=0,将AP,BP 写成双直线二次曲线:(9y-y0x-3y0)(3y-y0x+3y0)=0,因为A,B,C,D 是双直线二次曲线与椭圆的交点,联立方程:

图1

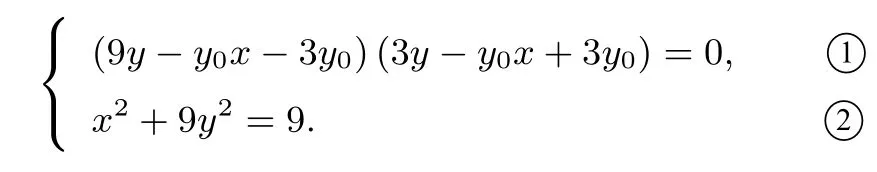
考虑到A, B 是已知的, 且纵坐标均为0, 则联立后的方程必有因式y - 0 = y, 于是将①式按y 整理得:27y2+(18y0-12y0x)y+(x2-9)=0.

由②: x2-9=-9y2,代入得: 27y2+(18y0-12y0x)y-9y2= 0, 即y(9y + (6y0- 4y0x) - 3y) = 0, 由于交点C, D 满足联立后的方程, 且纵坐标不为0, 于是C,D 满足方程9y + (6y0- 4y0x) - 3y = 0, 即直线CD的方程为: 9y + (6y0- 4y0x) - 3y = 0, 按y0整理得:-3y+(6-4x)y0+9y = 0, 令得定点

例2(2011 四川理21)椭圆有两顶点A(-1,0),B(1,0),过其焦点F(0,1)的直线l 与椭圆交于C,D 两点,并与x 轴交于点P.直线AC 与直线BD 交于点Q.

解(1)椭圆: 2x2+y2=2,直线l := 0 或=0

(2) 如图2, 由于Q 点纵坐标为0,于是本题即求P 点横坐标.

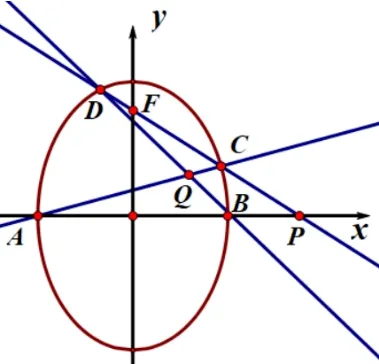
图2

设Q(m,n), 则lAC: nx-(m+1)y+n=0,lBD:nx-(m-1)y-n=0,将AC,BD 写成双直线二次曲线: (nx-(m+1)y+n)(nx-(m-1)y-n)=0,因为A,B,C,D 是双直线二次曲线与椭圆的交点,联立方程:

注例一例二都是通过构造双直线二次曲线,再利用其中两点坐标已知,求经过剩下两点的直线.其中已知两点的坐标,对联立之后式子的因式分解起到了指导性的作用.

2 变式运用

横向推广: 当双直线与圆锥曲线只有三个交点的时候,也可以用相同的原理求直线的方程.

(1)求C 的方程.

(2)设直线l 不经过P2点且与C 相交于A,B 两点.若直线P2A 与直线P2B 的斜率的和为-1,证明: l 过定点.

解(1)C 的方程:y2=1.

(2)如图3,设P2A 的斜率为k1,设P2B 的斜率为k2则lP2A: k1x-y +1 = 0,lP2B:k2x-y+1=0.

图3

将P2A,P2B 写成双直线二次曲线: (k1x-y+1)(k2xy+1) = 0,因为P2,A,B 是双直线二次曲线与椭圆的交点,联立方程:

考虑到P2是已知的, 且纵坐标为1, 则联立后的方程必有因式y - 1, 于是将①式按y - 1 整理得: (y-1)2-(k1+k2)x(y-1)+k1k2x2= 0,由②: x2= 4(1-y2),代入得: (y-1)2-(k1+k2)x(y -1)+4k1k2(1-y2) = 0,即(y -1)[y -1+x-4k1k2(y +1)] = 0, 由于交点A, B满足联立后的方程, 且纵坐标不为1, 于是A, B 满足方程y - 1 + x - 4k1k2(y + 1) = 0, 即直线AB 的方程为:y-1+x-4k1k2(y+1)=0,令得定点(2,-1).

注在考虑P2(0,1) 是已知的时候, 得出联立后的方程必有因式y-1,而不是x-0,因为x = 0 除了和椭圆有交点P2外,还有其它的交点, 而这个点并不是双直线与椭圆的交点.

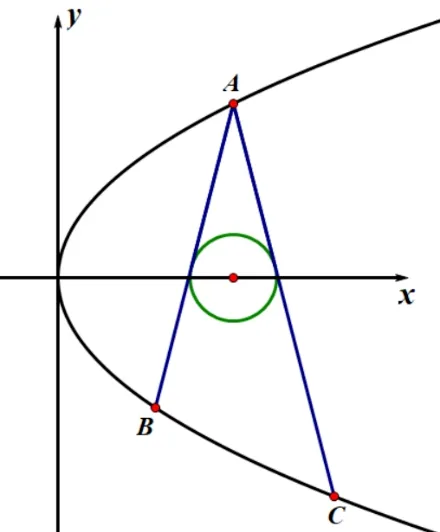
图4

例4(2021 八省联考7)已知抛物线y2= 2px 上三点A(2,2),B,C,直线AB,AC 是圆(x-2)2+y2=1 的两条切线,则直线BC 的方程为

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

注在考虑A(2,2)是已知的时候,得出联立后的方程必有因式y-2,而不是x-2,因为x=2 除了和抛物线有交点A 外,还有其它的交点,而这个点并不是双直线与抛物线的交点.

3 知识迁移

纵向联系: 做完这几道题,笔者不禁想起一道高考填空题的新解法:

例5(2009 海南宁夏理13)已知抛物线C 的顶点在坐标原点,焦点为F(1,0),直线l 与抛物线C 相交于A,B 两点.若AB 的中点为(2,2),则直线l 的方程为____.

解抛物线C : y2= 4x,设A(x1,y1),因为AB 的中点为(2,2),其对称点B(4-x1,4-y1)在抛物线上,将A(x1,y1),B(4-x1,4-y1) 代入C 得:展开即相减得y1= x1, 同理, 设B(x2,y2), 其对称点A(4 - x2,4 - y2) 也在抛物线上, 得y2= x2; A,B 均满足方程y = x, 于是直线l 的方程就为y =x.

注本题的解法很多,常规的解法是先求出直线的斜率,再写出直线的方程;上面的解法,则是利用了A,B 两点的地位对等(A 点满足其对称点在抛物线上,B 点也满足其对称点在抛物线上),从而可以构造关于A,B 两点坐标的一次式来求直线方程.

例6经过原点O 有一条直线l, 它夹在两条直线l1: 2x-y -2 = 0 与l2: x+y +3 = 0 之间的线段恰好被点O 平分,则直线l 的方程为____.

分析例6 与例5 的不同之处在于: 例五中A,B 地位是对等的,都是要让自己关于(2,2)的对称点在抛物线上;例6中,A 要让自己关于O(0,0)的对称点在l1上,B 要让自己关于O(0,0)的对称点在l2上,而l1,l2是不同的对象.为了让l1,l2变成统一的对象,把l1,l2写成双直线二次曲线F 的形式,从而让A,B 的地位对等,转化为了例5 的情形.

解记l1, l2组成的双直线二次曲线为F : (2x-y -2)(x + y + 3) = 0, 直线l 与F 的交点分别为A,B, 设A(x1,y1), 因为AB 的中点为O(0,0), A 关于O 的对称点B(-x1,-y1)在F 上,将A(x1,y1),B(-x1,-y1)代入F 得:展开即相减得: 12x1-6y1-4x1-4y1=0,即4x1-5y1=0,同理,设B(x2,y2),有4x2-5y2=0;A,B 均满足方程4x-5y =0,则直线l 的方程就为4x-5y =0.

圆锥曲线是高中数学教学中的一个重点、考试中的一个难点,通过对一类典型问题进行深入剖析、反思和一题多解,挖掘其潜在的价值,有利于培养学生发散性思维和综合运用数学思想方法解决实际问题的能力,从而达到掌握重点,突破难点的教学目的.