比较方差大小的几个结论及其应用
甘志国 (正高级教师 特级教师) 白 琨
(1.北京丰台二中 2.湖北省十堰市张湾区柏林镇中心小学)
由方差的计算公式可知,一组数据的方差与这组数据的每个数都有关系.因而,比较两组数据方差的大小要慎之又慎,不可妄下结论,比如,不能说“若极差大,则方差大”.本文给出比较方差大小的几个结论,用它们可迅速解决一些比较两组数据方差大小的问题.
令h=0,可得两组数据4,4的方差0 小于数据0,2的方差1;但数据4,4,1的方差2大于数据0,2,1的方差
推论2(1)若a≤b≤c≤d,则数据a,d的方差不小于数据b,c的方差(当且仅当“a=b且c=d”时两者相等);
(2)若a≤b≤c≤d≤e≤f,则数据a,e,f的方差不小于数据b,c,d的方差(当且仅当“a=b且c=d=e=f”时两者相等).
证明可用推论1中的(2)来证,下面只证(1).
当a<b≤d时,数据a,d的方差大于数据b,d的方差,所以当a≤b≤d时,数据a,d的方差大于等于数据b,d的方差(当且仅当a=b时取等号).同理,当b≤c≤d时,数据b,d的方差大于等于数据b,c的方差(当且仅当c=d时取等号),所以欲证结论成立.
定理3设a,α,n是已知的实数,α>na,n≥2,n∈N,且则当且仅当时,数据x1,x2,…,xn的方差取最小值且最小值是0;当且仅当x1=α-(n-1)a,xi=a(i=2,3,…,n)时,数据x1,x2,…,xn的方差取最大值.
证明下面只证关于“最大值”的结论.设数据x1,x2,…,xn的方差为.先证当n=2 时成立.由x1>a,x2≥a,x1+x2=α,可得a≤x2<α-a.又因为
从而可得当且仅当x1=α-a,x2=a时,取最大值.
再证当n≥3时成立.由引理,可得
在平面直角坐标系x2Oy中,抛物线
即证得了结论:设a,α,n是已知的实数,α>na,n≥2,n∈N,且
若数据x1,x2,…,xn的方差取最大值,则x2=a.
同理,可得结论:设a,α,n是已知的实数,α>na,n≥2,n∈N,且
若数据x1,x2,…,xn的方差取最大值,则xi=a(i=2,3,…,n),进而可得欲证结论成立.
定理4设x1,x2,…,xn均是给定的实数(且其平均数是a),x1,x2,…,xn,t(变量t取实数)的方差是f(t),则
(2)当t<(或>)a时,f(t)是减(或增)函数;当且仅当t=a时,f(t)取到最小值,且最小值是
定理5设x1,x2,…,xn,c均是给定的实数,则x1,x2,…,xn,a,b(a,b是变化的实数,但a+b=c)的方差随|a-b|的增加而增加.
证明由引理,可得x1,x2,…,xn,a,b的方差为
进而可得欲证结论成立.
例1(2020年全国Ⅲ卷理3)在一组样本数据中,1,2,3,4 出现的频率分别为p1,p2,p3,p4,且,则下面四种情形中,对应样本的标准差最大的一组是( ).
A.p1=p4=0.1,p2=p3=0.4
B.p1=p4=0.4,p2=p3=0.1
C.p1=p4=0.2,p2=p3=0.3
D.p1=p4=0.3,p2=p3=0.2
由“对称性”,可得这4组数据的平均数均是2.5.
把数据b与数据d中都去掉3个1、1个2、1个3、3个4后,剩下的数据分别是1,4与2,3,由推论2中的(1)可得前者方差大;再由定理1 中的(2)可得
例2甲、乙两名射击运动员参加某大型运动会的预选赛,他们各射击了5次,成绩(单位:环)如表1所示.

表1
易知数据8,9的方差小于数据10,7的方差,再由定理1中的(2)可得
例3甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩分别如表2、表3、表4所示.

表2 甲的成绩

表3 乙的成绩

表4 丙的成绩
若用s1,s2,s3分别表示甲、乙、丙三名运动员在这次测试成绩的标准差,则( ).
A.s3>s1>s2B.s2>s1>s3
C.s1>s2>s3D.s2>s3>s1
把甲、丙的成绩都去掉4个7、5个8、5个9、4个10后,甲、丙剩下的成绩分别为7,10与8,9,可得它们的平均数相等且前者的方差大于后者的方差,所以由定理1中的(2)知s1>s3.
综上,s2>s1>s3,故选B.
例4设两组数据A:-1,0,1,-1,0,1,-1,0,1,0与B:a,0,1,-1,0,1,-1,0,1,-1的方差分别为,求实数a的取值范围.
若a>0,由题设结合定理2可得,也即a<0,前后矛盾,舍去该情形.
若a<0,可得题设即“设两组数据B:-1,0,1,-1,0,1,-1,0,1,a与A:-1,0,1,-1,0,1,-1,0,1,0的方差分别为即a>0,前后矛盾,也舍去该情形.
综上,实数a的取值范围是∅.
例5已知实数x1,x2,…,x10满足x1>1,xi≥,求数据x1,x2,…,x10的方差s2的取值范围.
由定理3及引理,可得当且仅当x1=11,xi=1(i=2,3,…,10)时,有
再由题设中的方差s2是连续变化的,可得所求s2的取值范围是[0,9].
例6某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图1所示的茎叶图.
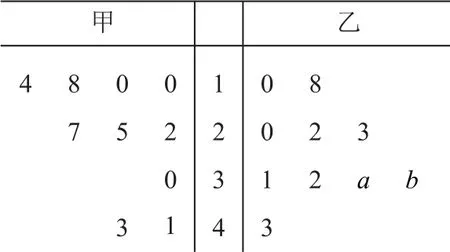
图1
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
若a=1,记乙型号电视机销售量的方差为s2,根据图1推断当b为何值时,s2达到最小值(只需写出结论).
但这种解法是不严密的:因为当b=0时,30+b与平均数
最近,但当b增加时,其他的数(比如43)与平均数的距离可能会近一些,这样就有可能使方差变小,所以以上解法并没有说清道理.
但由定理4可知,这种解法是“貌似无理,实则正确”.
例7(2012年北京卷文、理17,节选)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾,数据统计如表5所示(单位:t).
假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最大时,分别写出a,b,c的值(结论不要求证明),并求此时s2的值.
下面再看0,600-a,a(0<a≤600)的方差s2何时最大.
由定理5知,当且仅当|(600-a)-a|即2|a-300|取最大值,也即a=600时,方差s2最大,所以当数据a,b,c的方差s2最大时,a=600,b=c=0;还可求得此时s2的值是80000.
例8(2013年北京卷文、理16,节选)图2是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3 月1 日至3月13日中的某一天到达该市,并停留2天.
由图2判断从哪天开始连续三天的空气质量指数方差最大? (结论不要求证明)
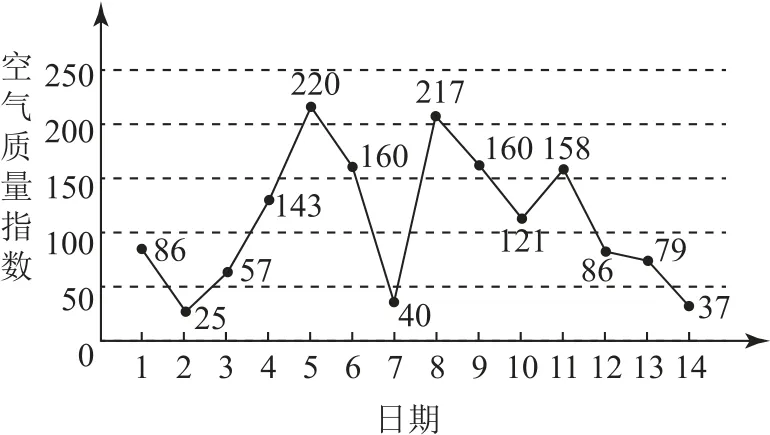
图2
s分别是两组数据57,143,220;40,160,220的方差.注意到这两组数据的平均数均是140,可得两组新数据57,143;40,160的平均数也相等,由推论2中的(1)知,前者的方差小于后者的方差,再由定理1中的(2)可得
s分别是两组数据220,160,40;158,86,79的方差,由40≤79≤86≤158≤160≤220及推论2中的(2)可得
注可能有读者用错误的结论“极差越大⇔方差越大”(反例:数据0,6,12的极差比数据0,10,11 的极差大,但前者方差小;数据20,3,12,15比数据0,3,12,15的极差大,但两者方差相等)迅速得到了正确答案,这当然是不严谨的.解答该题要进行必要的计算(包括估算)和推理.
可能有的读者会想,当两组数据的平均数相等时,结论“极差越大⇔方差越大”是否普遍成立呢? 答案也是否定的.若这两组数据的平均数相差正数ε,则可把平均数小的那组数据的各数均加上ε,得到的新数据的极差及方差均不变.
一组数据的方差反映的是这组数据的波动情况,但波动情况不仅仅是由极差决定的.由方差公式知,它与每个数据都有关.
(完)

