基于随机化的混沌单分组散列函数的设计与实现

■尹沧涛，李永珍

（1.延边职业技术学院，吉林 延吉 133000；2.延边大学，吉林 延吉 133000）

随着网络技术和电子商务的迅速发展，保护数据的隐私和安全已经成为了一项极其重要的任务。为了更好地保护数据的安全，密码学研究不断向前推进，引入了许多新的技术和方法。其中，哈希函数就是密码学领域中的一种重要技术。哈希函数是一种将任意长度的消息压缩到固定长度的技术，它的输出值称为消息的哈希值或摘要。哈希函数是一种重要的不可逆加密算法，从而保护数据的完整性和安全性。本文对MD5 算法进行改进，意在进一步保护短消息在传输和保存方面的安全性。

一、相关理论基础

（一）哈希函数及MD 系列

哈希函数是一种将任意长度的输入数据映射为固定长度输出的函数，哈希函数具有以下特性：唯一性、一致性、不可逆性、抗碰撞性。哈希函数在计算机科学和密码学中有广泛应用，例如，数字签名、消息认证、密码学中的密钥派生等领域。常见的哈希函数包括MD 系列、SHA 系列、RIPEMD等。MD系列是由美国密码学家Ronald Rivest 发明的一系列哈希函数，包括MD2、MD4、MD5 三种算法。这些算法都是基于Merkle-Damg rd 结构的迭代哈希函数，其核心思想是将消息分为若干个块，对每个块进行一系列的变换操作，最终得到一个固定长度的哈希值。

（二）混沌理论

混沌理论是一种研究非线性系统的数学理论，它最初被提出描述混沌现象，即一种看似随机无序、但实际上有规律的现象。混沌理论由李天岩和Yorke J A 于1975 年提出[1]。现已成为一个广泛研究的领域，涉及物理学、生物学、社会科学等多个领域，其具备下列特征：确定性、敏感性依赖、自相似性、稳定的随机性、非线性。

混沌系统的输出是非线性的、无规律的，并且受初始条件的微小变化而产生不同的结果，这些特性使得混沌系统的输出可以被用作密码学中的加密和解密。

目前混沌系统在密码学中的应用主要体现在哈希函数的改造上。通过混沌系统的改造，可以使哈希函数的输出更加随机和无序，从而提高哈希函数的安全性和抗攻击能力。

（三）随机化结构

目前，对哈希函数的传统攻击手段，如长度扩展攻击，第二原像攻击，中间相遇攻击等，都是以明确函数内部结构为前提。2004 年王小云教授等人提出了差分攻击，成功地对具有MD 结构的算法进行了有效的碰撞，这进一步增加了哈希函数的安全隐患。差分攻击是通过寻找哈希函数内部不同输入值之间的差异，破解函数的攻击方法。它利用哈希函数的差分特性，找出一些输入的差异，从而推导出哈希函数的输出差异。然后，通过这些输出差异，可以生成两个不同的输入，使它们在哈希函数中产生相同的输出，即碰撞攻击。但当哈希函数的算法是不确定的时候，密码分析将很难着手。对于一个固定的函数，要保证单向性是比较困难的，因为原则上可以根据哈希函数的结构进行逆推[2]。但是，在引入随机函数的情况下，哈希函数的表达式、结构和形式可能是随机的不确定的，因此，逆推哈希函数变得非常困难。

二、算法的设计与实现

（一）预处理阶段

本设计所提出的哈希函数为更好的适应短消息加密，将输入长度限制为1 bit 至128 bits。若不足128 bits，则填充1 个1 和多个0。将处理好的消息，分成A、B、C、D，4 组每组32 bits（见图1）。

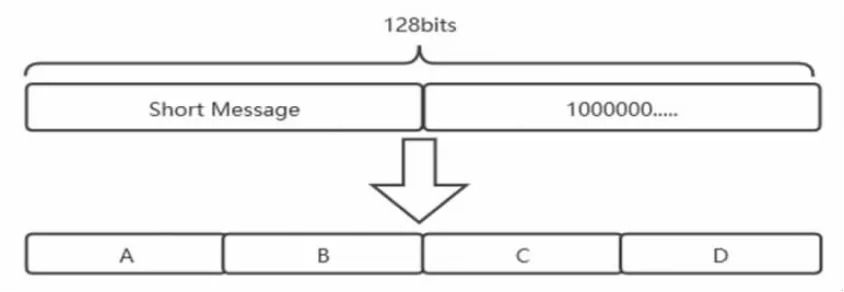
图1 算法的初始化过程

对于安全的哈希函数，在已知哈希值和算法的时候，明文（消息）m 本质上是可以推导的，但是通过哈希值计算明文的困难让我们通常地认为它是未知的，所以，如果哈希函数的具体形式由明文确定，即i=S(m)，哈希值H=fi(m)，则刚好满足上面提到的“已知明文可以很容易确定函数的具体形式，已知哈希值很难确定函数的具体形式”的要求。为减少计算量，存储量和复杂度，本设计在预处理阶段确定哈希函数的具体形式。将预处理后的128 bits 内容，分为两组M1 和M2，各64 bits。为消除预处理阶段M2 填充1 和大量0 后可能产生的规律性。将M1 左循环移6 bits，M2 右循环移8 bits 后异或，并对1024 取模，结果为10 bits 的2 进制数。前8 bits 中，每2 bits 控制第2 节主循环中一个逻辑函数的具体形式。后2 bits 将被保存，并用于第3 节中混沌加密算法及其分形参数的确定。

（二）主循环逻辑

算法的主循环共经过4 轮，每轮4 步的逻辑运算，一共经过16 步运算，最终生成长度为128 bits 的输出结果。将4 组待操作内容，分别与A，B，C，D 四个寄存器中的常量，按位与运算，在本步循环结束时获得的运算变量替换循环前所保存的寄存器变量，用来更新寄存器内容[3]。图2 描述了该算法主循环的整体逻辑。

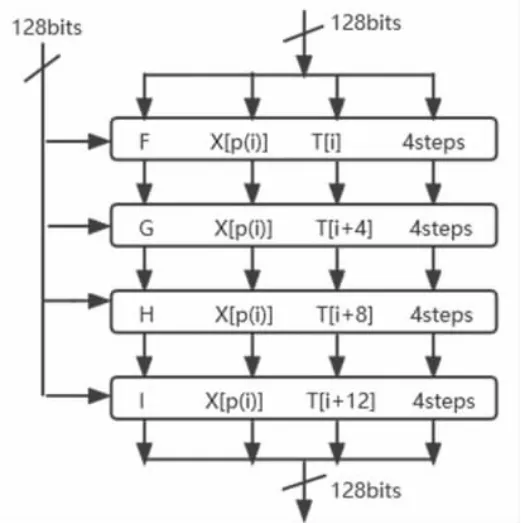
图2 整体逻辑图

其中，T 为128 bits 常数，其作用为对操作内容进行混淆，消除短消息内容上的规律性。F,G,H,I 为四个函数列表，内部各含有4 个不同的逻辑函数F=[f1,f2,f3,f4],G=[g1,g2,g3,g4],H=[h1,h2,h3,h4],I=[i1,i2,i3,i4]，每轮将选取列表中的一个函数参与4 步运算。

附表1 为随机函数的定义，新设计的逻辑函数保证了结果满足均匀分布的规律，从而确保循环后输出结果具有统一分布。X[p（i）]为不同轮中分组的使用顺序，p（i）函数具体形式如下：

附表1 随机函数定义表

第一轮中：p（i）=i；

第二轮中：p(i)=(1+5i)mod 4；

第三轮中：p(i)=(5+3i)mod 4；

第四轮中：p(i)=7i mod 4；

（三）混沌加密算法

由于混沌映射具有良好的随机性、初始值敏感性，与哈希函数设计原则极为贴切。因此，在过去几十年中，有学者曾提出过具有混沌映射构建哈希函数的方案[4-6]，本设计将利用多种参数可变的混沌加密算法，对循环后的结果通过迭代处理的方式产生新的输出值，以提高哈希函数的扩散性，整个混沌映射流程，见图3。

图3 混沌映射算法流程图

由图3 可知，为了将得到的A,B,C,D 四个寄存器的值转换为16 个混沌映射的初始值，并落在(0,1)的值域上，首先需做如下线性变换：

βi为消息分块后的ASCII 值。

定义可变参数的混沌映射算法如附表2 所示。

附表2 混沌映射定义表

这里将通过第2 节保存参数s，确定混沌映射的使用编号。本设计将μ 设为固定范围的可变参数，为克服周期窗口对混沌映射的影响，其确定方式如下：

随机参数μ 由线性同余随机数发生器（LCG）产生，选取的混沌变换将进行36 次迭代。其中K1,K2,K3,K4 为上一轮输出结果的分组，各32 bits。式（2）中233-1，根据文献建议进行取值，其为一个较大的奇素数，产生的随机数具有较大周期，保证了参数μ 的取值空间和随机性。

经过36 轮迭代计算，得到的混沌序列为：

对迭代结果x36（1），x36（2），…，x36(16)通过公式进行逆变换。

其中floor（x）为向下取整操作，舍去小数点后的值，以提高哈希函数的单向性。根据式（4）可得到16 个0 至255 之间的整数，每个整数用8 bits 的2 进制数表示，最终将输出128 bits 的结果。

三、实验测试与分析

本节首先进行混沌的判别分析，验证设计中的系统具备混沌状态；再通过统计分析、雪崩效应以及算法效率三个方面，进行对比试验，验证设计的安全性以及效率。

（一）混沌的判别原则

混沌运动是非线性系统特定的运动形式，但是系统的非线性仅是出现混沌运动的必要条件而非充分条件[7]。其判别多先用数值实验识别，再通过工程试验验证，实验将采用以下两种方式验证系统具备混沌状态，即李雅普诺夫指数法和分岔图法。

证明一动力系统或自治微分方程稳定性的函数被称为称李雅普诺夫指数(Lyapunov Exponent)，简称LE。它沿某一个方向取值的大小与正负可用来描述动力学系统的相邻轨道沿该方向的平均发散或收敛的快慢程度。正的李雅普诺夫指数越大，表示运行轨道越发散，使系统呈现出“既不收敛，也不发散，也不周期”的混沌态。一维李雅普诺夫指数计算公式如下：

其中λ 为李雅普诺夫指数，f(xi)为一维混沌映射函数。

分岔图法中“分叉”指的是当系统中的控制参数略有变化时，如果整个动力系统的结构不稳定，系统的拓扑结构会突然改变。对于某个特定的参数，状态变量在分叉图上呈现为一个点或与系统等周期的点，这表明系统处于周期状态；如果对于某个控制参数，分叉图上有无数个点，并且每次状态都不落在同一个点，则系统处于混沌状态。

1.Logistic 映射

图4 给出了Logistic 映射随分形参数μ 变化的李雅普诺夫指数图谱。从其图谱可见，当参数μ∈[3.57,4]时，该映射的李雅普诺夫指数大于0，进入混沌状态。图5 给出了Logistic 映射的分岔图，当参数μ 大于3.57 时映射取值范围逐渐增大，符合混沌特点。

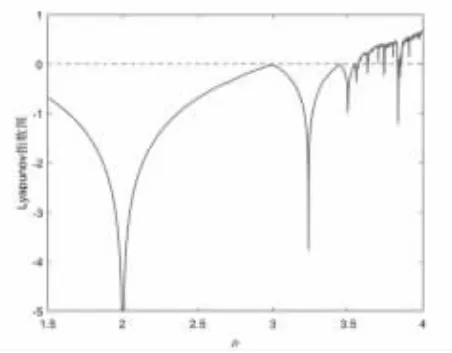
图4 Logistic 映射李雅普诺夫指数图谱

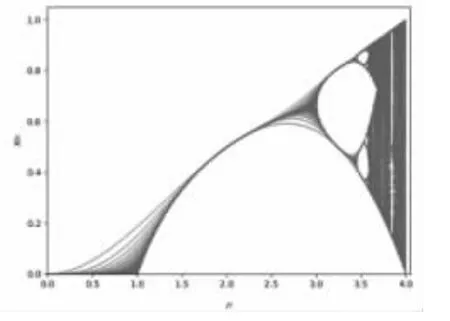
图5 Logistic 映射的分岔图

2.Tent 映射

Tent 映射常用于图像加密系统，由图6 可知，当参数μ 大于1 时，系统的李雅普诺夫指数皆大于0; 由分岔图（见图7）可知，当μ 大大于1.75 时，其取值范围接近满射。

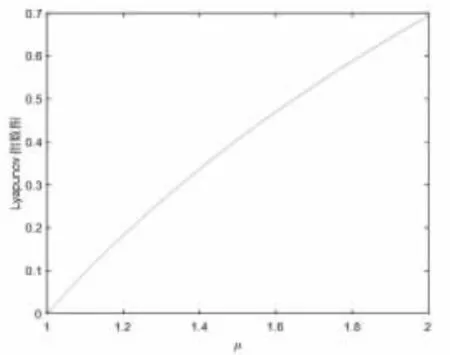
图6 Tent 映射下μ 的李雅普诺夫指数图谱

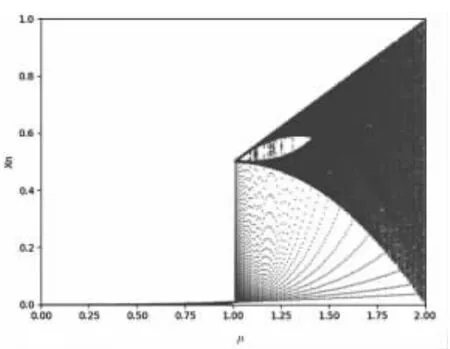
图7 Tent 映射下分岔图

3.Tent 映射

从图8,9 中可见Chebyshev 映射的参数区间更大，李雅普诺夫指数也更大，说明其混沌性优于前两者。当分形参数μ 大于1 时进入混沌状态，大于2 时即可遍历该区域所有状态点。

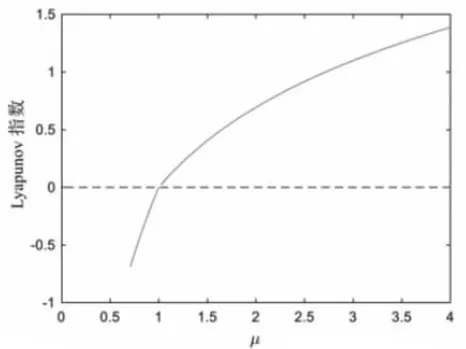
图8 Chebyshev 映射李雅普诺夫指数图谱

图9 Chebyshev 映射分岔图

4.Sine 映射

Sine 映射是混沌映射的典型代表，它的数学形式极为简单，由图10、图11 可知当分形参数μ 大于0.87 时，其进入混沌状态。

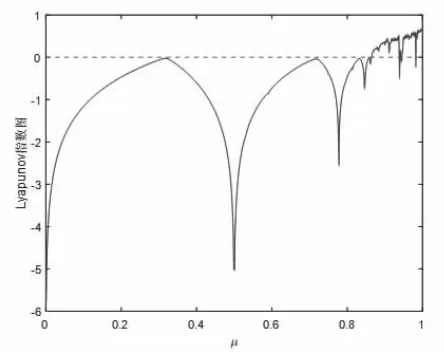
图10 Sine 映射李雅普诺夫指数图谱

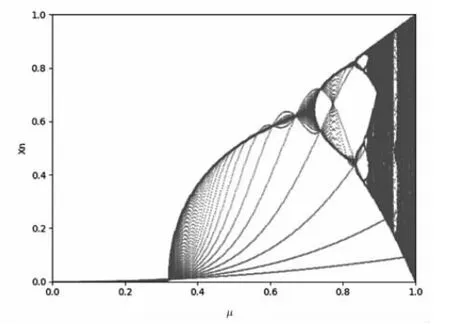
图11 Sine 映射分岔图

由上述实验可知，本设计中可变参数μ 的取值范围皆符合混沌要求，可通过迭代计算的方式，将消息通过处理得到的哈希值扩展到整个向量空间。

（二）统计分析

为确保哈希函数的安全性，要求其值域是均匀分布的，否则，攻击者就能够以低于暴力破解的代价找到哈希函数的碰撞[8]。本设计选取以下六个指标对哈希算法进行统计分析。

（1）最大变化比特数Bmax；

（2）最小变化比特数Bmin；

测试方法如下：首先选取1000 个长度介于1 bit 至128 bits 的短消息，计算输出结果，再翻转消息中任意1bit，计算改变后的输出结果，将两者对比得到结果，如附表3 所示。

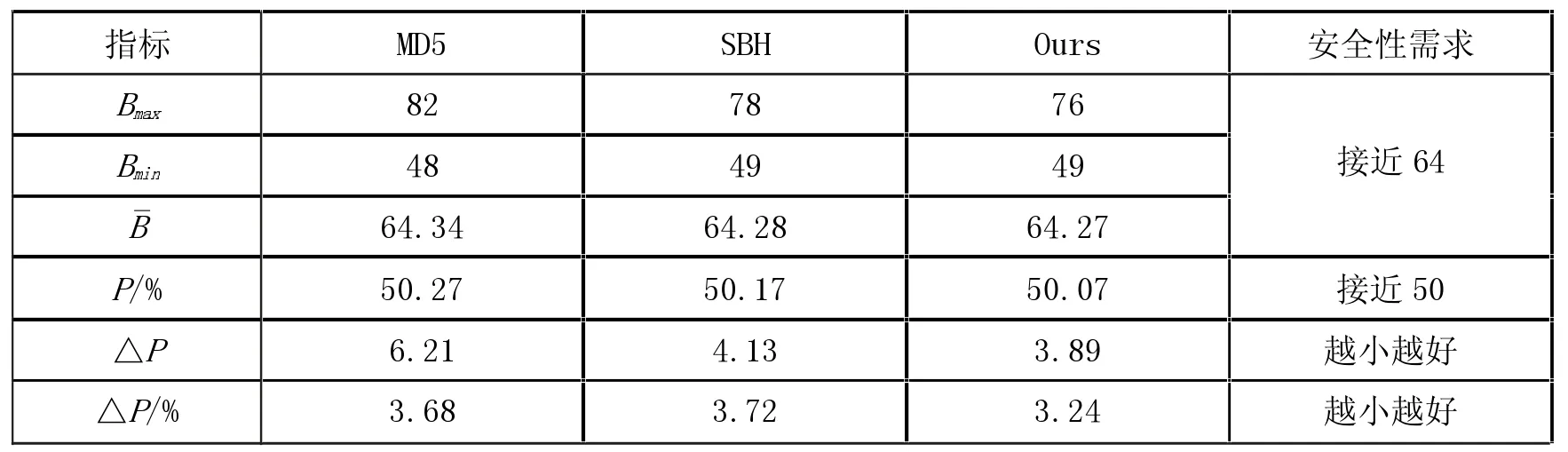
附表3 统计分析结果

由统计测试结果可以看出，本设计提出的哈希函数平均变化比特数比传统算法更接近于理想值，平均变化概率P 也非常接近于50%，平均变化比特数的均方差△B 和平均变化概率的均方差，P 均比传统算法小，说明其变化幅度很小且非常稳定，同时Bmax和Bmin也较小。统计分析结果表明，本设计具有良好的抗统计攻击能力。

（三）雪崩效应

哈希函数不同部件的数据关系越独立，则越容易在密码分析的过程中被逐个击破。因此，良好的雪崩效应是一个优秀的哈希算法所应该具备的。实验按照雪崩效应的原理来设计实验，使用1000 对明文对，这些明文对每个都只有一位不同，通过比较两个明文经过算法得到的结果中不相同的位数，来作为评判标准[9]。按照雪崩效应所描述的，其理想值应接近输出结果位数的50%。

图12—图14 为本设计提出的算法与传统算法的雪崩效应实验结果，这里规定百分比大于60%的点和小于40%的点为坏点。经过统计发现各个算法坏点出现的概率如下。MD5：3.2%；单分组哈希函数SBH：2.25%；本设计提出算法：1.82%，从统计结果可以看出，添加具有随机化参数的混沌映射使结果行成高度关联、广泛扩散的状态，有效的提高了哈希函数的雪崩性和扩散效果。

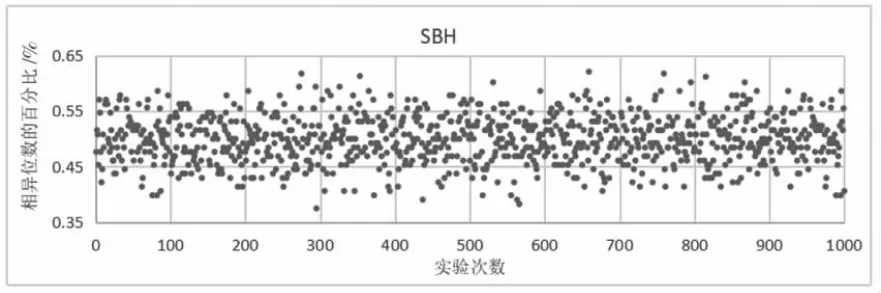
图12 SBH 雪崩测试结果

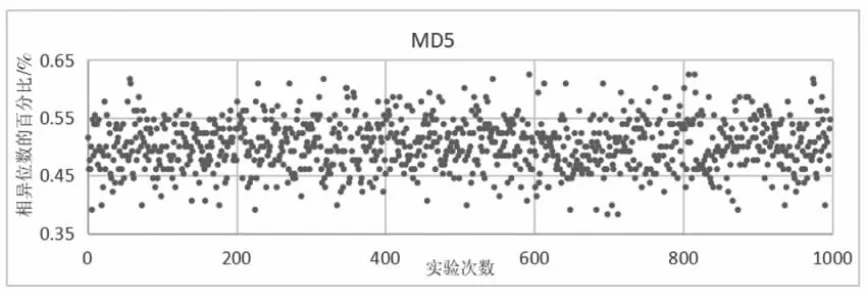
图13 MD5 雪崩测试结果

图14 Ours 雪崩测试结果

（四）效率分析

为通过累加每次运算的时间，将时间尺度拉大，使结果便于观察，在算法效率测试中，每个算法都需要运行10000000 次，在实验过程中，每次输入长度为128 bits且各不相同的消息，图15 为效率对比结果。

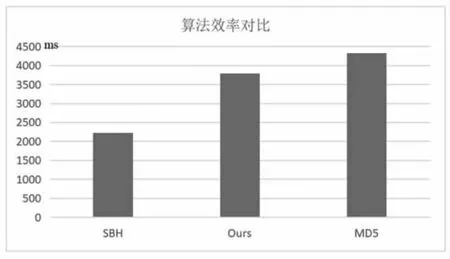
图15 算法效率对比结果

从实验结果可以看出，本设计提出的算法与SBH算法相比运行时间增加到了169%，与MD5 相比运行时间减少到了86.9%。由于本设计在迭代过程中引入36 步混沌映射，所以运算效率低于SBH 算法，但从结果可以看出，其依旧保留良好的密码学算法所需的线性特性。

四、结语

本设计提出了一个针对处理短消息的哈希函数，通过引入随机化的思想，使攻击者在仅知到输出结果的情况下，无法确定哈希函数的具体形式，提高了哈希函数的单向性，从而加大了攻击难度。同时，通过多种可变参数的混沌映射，有效的解决了SBH 算法由于迭代次数过少，无法进行有效扩展的问题。由于其属于线性运算，有效的保证了算法的运行效率。综上所述，本设计在保证算法效率的前提下，可以有效地保障短消息在处理过程中的完整性以及安全性。