在操作中建构数学模型

江苏南通市港闸区唐闸小学 郭 祥

在操作中建构数学模型

江苏南通市港闸区唐闸小学 郭 祥

《义务教育数学课程标准》（2011年版）明确地将“模型思想”列为核心概念之一，这是当今社会对义务教育阶段的数学教学提出的新课题和新要求。在广义模型观下，数学就是关于模型的科学，学生的数学学习本质上就是对数学模型的认知以及建模过程的经历与经验的积累。数学模型的抽象性与小学生以形象思维为主的认知特征，是数学建模教学中一对突出的矛盾，化解矛盾的方法是多元的。其中，通过学生实践操作化解矛盾，效果显著。

一、在操作中诱发模型意识

著名教育学家苏霍姆林斯基曾说过：“儿童的智慧就在他的手指尖上。”那么，由“指尖”抵达“智慧”的通道是什么呢？让学生面对现实的数学问题，在内心产生疑惑与探究的欲望，积聚操作的内驱和势能，让操作成为学生内心深处的一种需求，而不是外在的指令要求，是一则良策。

如《三角形三边关系》的教学，三角形是由三条线段围成的图形，反过来，提供三条线段是不是就一定能围成一个三角形呢？对此，学生或肯定，或否定，或心存疑惑，此时用小棒替代线段来围一围的操作自然成为学生验证自己内心想法的一种强烈需要。在选择长短不同的小棒围三角形的尝试中，学生会主动发现：同样是三条线段，有时能围成三角形，有时则不行。这是为什么呢？操作结果势必诱发新的探索：“怎样的三条线段才能围成三角形呢？怎样的则围不成？”学生的探索自然会汇聚到一点——三角形三边关系的数学模型上。从4厘米、5厘米、6厘米和10厘米的四种小棒中，选择三根小棒动手操作、观察记录和比较交流，发现三角形任意两边长度的和大于第三边。

显然，真正建立在学生内在需求基础上的数学活动，能够有效诱发学生对数学模型的思考与探索；翔实的操作体验和深层的认知需求协同作用下的数学活动，是学生主动建构数学模型的一条重要途径。

二、在操作中丰富模型体验

概念作为一种数学模型，尤为抽象，学生不易理解，难以掌握，也容易混淆。教学时，教师应尽量将抽象的概念做具体的、形象化的演绎，将静态的描述转化为动态的操作过程，让学生的思维发源、依托并超越操作活动。通过操作获得直接的感性体验与认识；在有层次、多维度的操作体验中逐步丰富表象、感悟属性；凭借“操作—思维，思维—操作”的不断往返交替与螺旋上升，助推学生对数学模型的本质领悟与理解。

如《认识周长》的教学，是要引导学生在二维平面图形中研究一维长度的概念，对学生而言具有认知上的挑战，其关注点和思维都难以聚焦，认识也难以清晰、到位和深刻。需要引导学生利用并顺应先前认识图形的经验与顺序——由体到面，做进一步的递推，再由面到线逐步建立起一周边线长度——周长的概念。教学中应引导学生经历一些必要的操作活动，借助学生熟悉的素材体验“做中学”。首先，让学生把自己喜欢的卡通贴画的边缘描一描，并从卡片上剪下来，剪好后同桌互相指一指、说一说：“你沿着什么剪的？从哪里剪到哪里？卡通贴画的边缘，也就是边线在哪里？”在描、剪、指、说的过程中体会“边线” “一周”的含义。接着，让学生在小组里指一指、说一说书本、课桌、树叶、硬币等物体表面的“一周边线”，并且比较它们的长短；再让学生独立描一描平面图形（长方形、三角形、半圆形、不规则图形）的边线，帮助学生从实物到平面图形，完整地建立对 “一周边线长度”——周长的理解。最后，再设法让学生量一量树叶的周长、树干的周长，在化曲为直，从平面到立体的变式、拓展的操作体验中，丰富和完善对周长概念的本质理解。

概念教学的两个关键点，一是要让学生准确把握其内涵，二要让学生厘清、界定其外延。由于二者往往会交织于概念模型形成的过程之中，常常需要通过分层操作、专项操作让学生在丰富模型体验的基础上完善、深化对模型的认知。

三、在操作中生成模型表征

现代心理学认为，思维的发展一般要经历“直观动作思维→具体形象（表象）思维→抽象逻辑思维”这样三个阶段。

学生的操作过程是一种思维的外化过程，常常能够助推其直觉思维和具体形象（表象）思维；学生在操作过程的体验，对操作经验的积累，以及基于操作结果的分析与感悟，常常会内化为他们头脑中的表象或图式。随着表象的不断丰富和逐步精致化，则会进一步深化为理性经验和认识，实现图式表征到意义表征的飞跃。

如《搭配的规律》的教学，出示图片信息：2件上衣和3条裤子；呈现问题：一件上衣与一条裤子搭配，一共可以有多少种不同的穿法？先让学生借助实物图片摆一摆，通过实践操作获得直观经验；再把自己的想法设法在本子上表达出来；然后合作交流，展示不同的数学思考：有的用文字一一列举，有的用符号（字母、数字、图形等）来表达，还有的用连线方式呈现……最后，通过比较、概括达成共识——用连线的方式表达 （如图1）。这种几何直观的图式兼具形象性和过程性，在后续解决类似于“4个素菜与2个荤菜，1个荤菜搭配1个素菜，有几种不同的搭配方法”之类的问题时，学生便能运用。

搭配图式是一种直观化的操作模型，它还有待于进一步地抽象概括，成为更为上位的具有一般性、概括性的符号化的数学模型。如将上述搭配图式提升为乘法原理的数学模型：这类图式还可以用来解决什么问题？如果上例变成20件上衣和30条裤子，运用搭配图式还方便吗？能改用一个数学式子来表示吗？（20×30）此类问题的解决能有一个通用的模式吗？（a×b）在搭配图式的运用与拓展中，乘法原理的数学模型水到渠成。

图1

操作活动常常起始于某个特定的情境和特定的实物，但不能仅仅止于操作过程的经历和结果的获得，也不能只停留在直观感性和直觉思维层面。实施操作活动以后，要有意识地引导学生就自己操作的所获所感进行个性化的表达交流，通过比较、分析，强化对表象的认知，并利用表象架设桥梁，通过对表象的符号化、数学化，实现操作活动的思维内化，逐步建构学生头脑中关于操作过程和结果的数学模型。

四、在操作中完善模型建构

学生在操作活动中需要获得的不仅仅是数学知识和技能，更重要的是经历探索的过程，学习和掌握研究数学的思维模式与思想方法，体验知识“再创造”的过程。其间，常常要以操作的阶段性结果为基础，做进一步的分析思考、猜想验证、交流切磋，实现数学模型的逐步修正、拓展与完善。

如《钉子板上的多边形》的教学，首先明确研究方向：边上的钉子数与图形的面积的关系（如图2）。然后，通过观察填表、分析数据，形成阶段性研究成果（多边形的面积是边上钉子数的一半，即S=n÷2）。接着，学生在钉子板上自由构图，验证所发现的规律，并引发冲突（如图3）：“为什么先前发现的规律在这里不适用了呢？”通过操作、比较发现：当图内只有1枚钉子时，即当a=1时，S=n÷2。

图2

图3

“当a=2时，多边形的面积又是多少呢？”小组合作在钉子板上边围边研究。学生运用前期研究成果，迁移先前操作活动经验，得出当a=2时，S= n÷2+1。据此发散：当a=3、4……时呢，有规律吗？能一一验证吗？需要一一验证吗？有什么规律？探索活动从动手操作的有限层面跃升到类比推理的无限境地，学生亲身经历类似数学家研究问题的过程，通过操作、思辨、猜想、验证、推理活动，自主探究、发现数学，逐步修正、拓展与完善数学模型，获得“操作—发现—推理”的数学学习与探索的方法启迪和历练。

五、在操作中助推模型升级

操作活动不只是单纯的“动手”实践，其核心价值在于对学生数学思维的启迪与促进，实现外显动作与内隐思维的双向互动，促使“操作的思维”和“思维的操作”螺旋上升。以问题解决为行为驱动，以操作过程和阶段性结果为思维载体，通过观察、比较、交流、反思等活动，不断实现对已有数学模型的创造性改造，逐步创生出新的数学模型。

如《复式统计表》的教学，根据单式统计表（如图4）进行数据的收集与整理。然后分析数据，回答“哪个兴趣小组男生最多？四个兴趣小组是男生多还是女生多”等问题时，发现往复观察、比较的不便，产生组合、重构新的统计表的需求。学习小组在思考中操作，在操作中思考，有的把4张单式统计表纵向排列（如图5），以解决数据对比不便的问题；有的在将四表第一横栏合并（如图6）后，发现数据对比十分方便，但同时产生了数据与组别无法对应、标题如何合而为一等矛盾；有的则更进一步，提出交代男生总数、女生总数以及总人数的设想……学生操作、反思、重构，最终形成复式统计表，从而实现了对数学模型的改造升级。

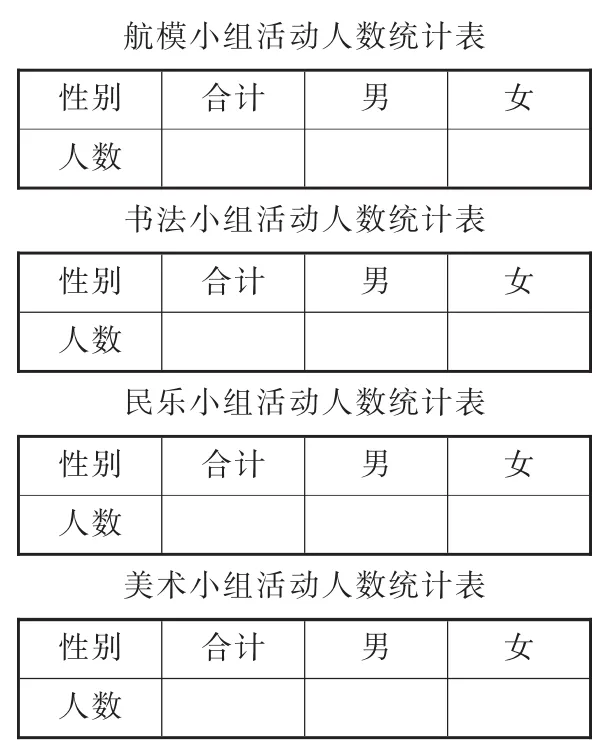
图4

图5

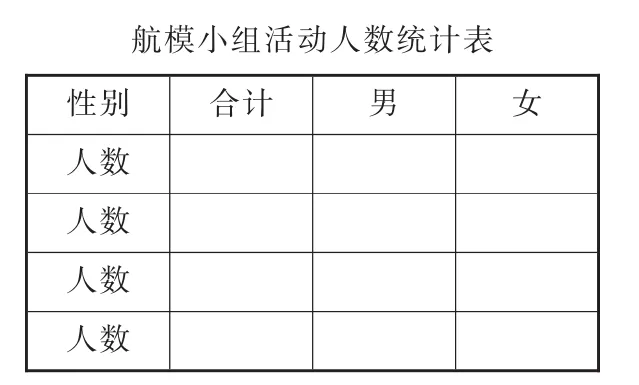
图6

学生的操作活动应发端于内心深处的实际需要，教师要以适切的问题情境诱发学生产生操作内驱，同时要为学生提供必要的时、空、物等操作平台，更要设法将教学目标——数学模型的建构，内化为学生解决问题的操作（行为的、心理的）指向。