巧用几何画板 妙求定点定值
——以一道高考题为例
蔡珍珍 汪国红
(湖北省武汉市第二十三中学,430050)
随着信息时代的到来,教学手段日趋多样化,几何画板软件越来越被广大教师和学生所接受,给数学教学中的“数形结合”带来便利,也为数学教学提供新的实验平台,它巨大的图形构造和处理功能使数学教学更加生动.但几何画板不仅仅是处理图形的工具,更是探究问题、分析问题的导向.本文以一道2020年高考试题为例,借助几何画板进行探究.
一、真题再现

(1)求E的方程;
(2)证明:直线CD过定点.

二、直观辅助,大胆猜想,培养直观素养

三、几何画板助力,追根溯源,培养探索精神
(1) 通过几何画板制作动画,在直线l上移动点P,发现直线CD过x轴上一定点M,经过图1推断猜想成立.

(2) 进一步猜想:点M的横坐标与t有关系,通过利用几何画板制作动画,观察发现在椭圆方程不变的情况下,移动椭圆和直角坐标系,点P与点M的横坐标乘积为定值,且定值只跟椭圆的长轴长有关,如图1,2.

四、演绎推理,揭示本质,培养理性思维





五、细致观察,控制变量,培养逻辑素养和创造思维

通过几何画板作出图4,5,将直线CD绕点M旋转或在x轴上移动点M的过程中,观察可知点P的轨迹为定直线,且该直线垂直于x轴,满足xP·xM=a2.


通过几何画板作出图6,7,当点P在垂直于x轴的直线上运动时,观察可知直线CD过x轴上定点,且满足xP·xM=a2.

六、类比学习,拓展思维
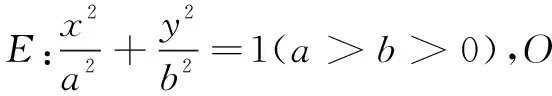
(1)求椭圆的方程;
(2)直线l:y=kx+t与椭圆C交于两个不同的点M,N.已知点M关于y轴的对称点为M′,点N关于原点O的对称点为N′,若A,M′,N′三点共线,求证:直线l经过定点.

(2)直线l恒过定点(-1,0).
1.直观演示

① 通过几何画板制作图象,将直线绕点A旋转,如上图8可知,在旋转过程中发现直线MN过x轴上一定点;改变点A坐标和直线l,发现点A和点P的横坐标之积为定值,如图9.
② 改变点A坐标和直线l,发现点A和点P的横坐标之积为定值,如图10、11.

2.演绎推理

1(a>b>0),点A是x轴上一定点,直线l与椭圆C交于两个不同的点M,N,已知点M关于y轴对称点为M′,N关于原点O对称点为N′,若A,M′,N′三点共线,那么直线l过x轴上一定点P,且xA·xp=-a2.

(*)
∵A,M′,N′三点共线,∴(-x1-t,y1)∥(-x2-t,-y2).∴(-my1-s-t)(-y2)=y1(-my2-s-t),即2my1y2+(s+t)(y1+y2)=0.代入(*)可得2mb2(s2-a2)+(s+t)(-2b2ms)=0,∴st=-a2得证.
圆锥曲线是历年高考考试难点,学生在计算、知识总结和题型归纳上比较困难.在教育教学过程中,要抓住“数形结合”的特点,利用图形的几何特征加强学生对知识的理解和认识,更好地培养学生直观想象能力. 几何画板软件是在数学实验中一款非常实用的工具,通过几何画板可以更加快捷地找到解析几何题型的规律,大大增加得出正确结果的概率.
——从广州一模的一道选择题谈起

