与指数函数、对数函数有关的最值(值域)问题

■陈 敏 张启兆

求与指数函数、对数函数有关的最值(值域)问题的关键是转化与化归思想的应用,下面归类举例说明此类问题的求解方法。

一、求函数的最值

例1设函数f(x)=logax(a>0 且a≠1)的图像经过点(2,1),当时,求函数的最值。

解:由函数f(x)=logax(a>0且a≠1)的图像经过点(2,1),可得loga2=1,解得a=2,所以函数f(x)=log2x,且定义域为{x|x>0}。

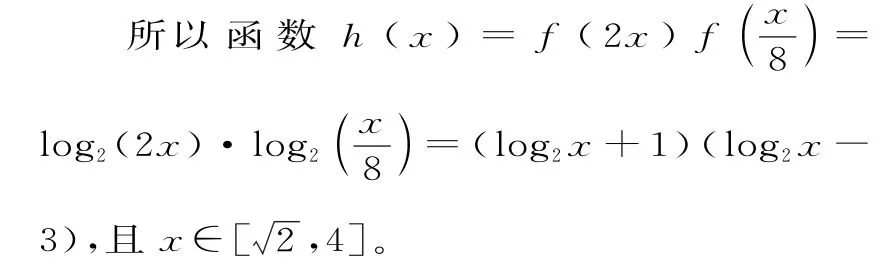
因为函数g(t)在上单调递减,在t∈[1,2]上单调递增,所以h(x)min=g(t)min=g(1)=-4。

故函数h(x)的最大值为-3,最小值为-4。

评注:解答本题的关键是通过换元变形,将原问题转化为熟悉的一元二次函数在区间上的最值问题,再借助“配方”变形即可得到最值。

二、求函数的值域

例2已知函数f(x)=log3x+1,x∈[1,9],求函数h(x)=[f(x)]2+f(x2)的值域。

解:因为函数f(x)的定义域为[1,9],所以解得1≤x≤3,即x∈[1,3],所以函数h(x)=[f(x)]2+f(x2)的定义域为[1,3]。

h(x)=[f(x)]2+f(x2)=(log3x+1)2+log3x2+1=(log3x)2+4log3x+2。设t=log3x,因为x∈[1,3],所以t∈[0,1],所以函数h(x)等价于函数φ(t)=t2+4t+2=(t+2)2-2,且φ(t)在t∈[0,1]上单调递增。当t=0,即x=1时,h(x)取得最小值,可得h(x)min=φ(0)=2;当t=1,即x=3 时,h(x)取得最大值,可得h(x)max=φ(1)=7。故函数h(x)的值域是[2,7]。

评注:求函数y=[f(x)]2+f(x2)的定义域时,容易忽视1≤x2≤9的情况。在复合函数中,外层函数的定义域是内层函数的值域,若已知f(x)的定义域为[a,b],其复合函数f[g(x)]的定义域可由不等式a≤g(x)≤b解出;若已知f[g(x)]的定义域为[a,b],求g(x)的定义域,相当于x∈[a,b],求g(x)的值域(即f(x)的定义域)。

三、由给定的最值,求参数的值

例3设函数f(x)=ax-a-x(a>0且a≠1)。已知,函数g(x)=a2x+a-2x-2mf(x)在区间[1,+∞)上的最小值为-2,求实数m的值。

解:依题意得。因为a>0且a≠1,所以a=3,所以函数f(x)=3x-3-x,所以函数g(x)=32x+3-2x-2m(3x-3-x)=(3x-3-x)2-2m(3x-3-x)+2,且x∈[1,+∞)。

令t=3x-3-x,由函数t=3x-3-x在[1,+∞)上单调递增,可得,即t∈

评注:利用恒等式(ax-a-x)2=a2x+a-2x-2进行转化是解题的关键。

四、由给定的值域,求参数的取值范围

例 4 已 知 函 数f(x) =若f(x)存在最小值,则实数a的取值范围是( )。

A.(-∞,4] B.[-2,+∞)

C.(-∞,-2) D.(-∞,-2]

解:已知函数当x<4时,f(x)=2x-a的值域是(-a,16-a);当x≥4 时,由f(x)=log2x,可 得f(x)min=2。

由题意知,f(x)存在最小值,所以-a≥2,解得a≤-2,即实数a∈(-∞,-2]。应选D。

评注:准确理解指数函数和对数函数的图像与性质,有助于顺利破解与指数函数和对数函数有关的最值(值域)问题。

(1)若对任意的x∈R,f(x)>0恒成立,求实数m的取值范围。

(2)若函数f(x)的最大值为2,求实数m的值。

(3)若对任意的x1,x2,x3∈R,均存在以f(x1),f(x2),f(x3)为三边长的三角形,求实数m的取值范围。

提示:(1)因为对任意的x∈R,f(x)>0恒成立,所以,可得9x+m·3x+1>0,即恒成立。

因为3x>0,所以,当且仅当x=0时取等号,所以-m<2,可得m>-2,即实数m∈(-2,+∞)。