微纳挠曲电结构力电耦合响应的数值模拟方法

黄怀纬 黄海博

（华南理工大学 土木与交通学院，广东 广州 510640）

机电耦合指的是机械运动和电磁现象之间的相互作用。其中挠曲电效应是现代高性能电子线路和微机电系统（MEMS）等领域的一个重要功能模块。它描述的是应变梯度诱导的电极化现象（正挠曲电效应）和电场梯度诱导的机械应变现象（逆挠曲电效应）。梯度在挠曲电效应中起控制作用。材料尺寸减小且应变不变时，梯度与材料尺寸成反比，这意味着微小尺寸的材料具有更大梯度，故而挠曲电效应也更显著。由于应变梯度与电场梯度的尺度效应，挠曲电材料在微纳米尺度下的高灵敏度传感［1］及精准致动［2］极具应用潜力。另一方面，相比压电材料，挠曲电材料普遍不需要经历苛刻的极化过程，也不会因温度达到居里点而丧失机电耦合效应，这有效增长了材料的使用寿命［3］。例如，将Gohari 等［4］提出的智能圆柱体压电辐射声音控制器改为使用挠曲电材料，可以在极端条件下正常工作。具有挠曲电效应的材料非常广泛，所有介电材料都可以表现出挠曲电性。本研究提供了有效分析挠曲电结构的方法。

固体材料中挠曲电理论框架完善的过程是漫长的。Mindlin［5］针对电介质提出考虑极化梯度效应的变分原理；Maugin［6］针对介电体建立了电场梯度理论；而后，Maranganti 等［7］给出了非压电材料力电耦合效应的一般理论框架。Sahin等［8］给出了考虑应变梯度与极化梯度效应的介电材料变分原理。Kalpakides等［9］发展了包含应变梯度和电场梯度的计算理论。Shen等［10］提出针对纳米电介质的电焓变分原理，为挠曲电材料的有限元计算提供依据。

挠曲电研究领域的迅速发展使数值模拟的需求日益加剧。然而由于应变梯度和极化梯度的存在，固体电介质中的挠曲电效应由四阶偏微分方程控制。传统仅基于位移的有限元法不适用于处理挠曲电固体。与应变梯度弹性一样，挠曲电本构方程在有限元中建模困难的问题由位移场近似值中C1单元连续性（函数及其一阶导数的连续性）造成。这个问题首先由Abdollahi等［11］使用局部最大熵（LME）无网格方法解决。等几何分析（IGA）对高阶连续性直接处理，是另一种可靠的挠曲电计算方法［12］。另外，如Yvonnet 等［13］的工作一样，Argyris 三角形单元也可用作C1单元连续性要求的补救措施。类似于应变梯度弹性，Mao等［14-16］采用混合有限元法来解决挠曲电问题。Tian等［17］提出用配点法处理混合元。

近年来，纳米尺度下挠曲电梁因其应变梯度大、电响应亦较强等优点，在能量采集、传感研究领域备受关注［18］。Hosseini 等［19］分析了深、浅弯曲功能梯度纳米梁的自由振动特性。Arefi 等［20］研究了压电双弯曲纳米壳的非局部高阶电弹性弯曲。Sladek等［21］建立了铁木辛柯梁模型用于分析开路状态下小曲率弯曲纳米梁的挠曲电效应。

MFEM 与当前大多数有限元代码的框架兼容。基于FORTRAN语言编写UEL子程序，在Abaqus中实现挠曲电材料的本构行为。用户自定义变量（UVARM）子程序用于传递计算过程中的状态变量，实现计算结果可视化。本文编写CMFEM通过C0单元来捕获C1 单元的连续性，相对于传统拉格朗日方法使用的9 节点高阶单元，简化了计算的同时，又保持了C1 单元的连续性。它避免了引入拉格朗日乘子的额外自由度，并将单元自由度从文献［14］中提及的87 个减少到12个，从而极大地提升了求解器的运算效率。

通过这一工作，将挠曲电材料本构模型的二次开发代码内化到Abaqus 程序中，实现了对挠曲电结构响应行为高效、准确的模拟。

对于挠曲电纳米结构已有一些讨论，然而商业有限元软件中挠曲电仿真方法仍然有待探索。主流有限元仿真软件中挠曲电相关的模块需要通过二次开发写入挠曲电本构方程。为此，本研究于Abaqus中开发了一个使用CMFEM 的UEL 子程序模拟挠曲电纳米结构，推导了包含挠曲电效应的力电耦合本构方程和数值方程。通过与现有成果对比，验证了UEL子程序并分析了网格收敛性；并以挠曲电纳米梁为数值案例，在Abaqus 中数值模拟了不同边界条件下的矩形纳米梁和弧形纳米梁的力电耦合响应。

1 基本理论

1.1 挠曲电本构方程

根据Shen 等［10］提出的考虑应变梯度和应力梯度影响的机电耦合理论，线性电介质体中的电焓密度表示为

式中，aij为二阶介电常数张量，cijkl为四阶弹性常数张量，ekji和fijkl分别为压电系数和直接挠曲电系数，张量gjklmni为应变梯度弹性的高阶弹性系数，dklij和hijkl分别表示逆挠曲电系数和高阶电参数，εij和εkl为应变张量，Ei、Ej和Ek为电场矢量，ηjkl、ηmni为应变梯度张量，Ei，j和Ek，l为电场梯度张量。

根据电焓密度表达式，本构方程可改写为

其中σij、Di、τjkl和Qij分别为应力张量、电位移张量、高阶应力张量和高阶电位移张量。高阶弹性参数gjkmni=l2cjkmnδli，与一般弹性刚度系数cjkmn、内部长度材料参数l和克罗内克函数δli相关［22］。同样，高阶电参数hijkl=q2aikδjl，由介电常数aik、另一个材料长度参数q和克罗内克函数δli组成。挠曲电系数fijkl=f1δjkδil+f2(δijδkl+δikδjl)，仅由两个独立分量f1和f2表征。与直接挠曲电系数fijkl类似，逆挠曲电系数dklij=d1δijδkl+(δikδjl+δilδjk) (d2δkiδlj+d3δkjδli)由3个独立的系数d1、d2和d3组成。

结合平面应变假设，将正交各向异性材料的本构方程改写为矩阵形式：

1.2 数值方程

Hu 等［23］根据虚功原理推导出梯度理论中有限元的变分公式为

式（5）右端为外力功，其中，tˉi、Rˉi、Sˉ、Zˉ分别表示力的密度、应力密度、电荷和高阶电荷，δui、δsi、δϕ、δp表示位移的变分、应变的变分、电势的变分、电场的变分，Γt、ΓR、ΓS、ΓZ为对应边界。

机械位移和电势可以用形函数Na表示：

其中，x表示有限元V上的节点，ξ1、ξ3为有限元V上的局部坐标系，a为高斯积分点，{qa}和ϕa分别是节点位移和电势。

在有限元V内，全局坐标中的梯度可由雅克比矩阵J表示为

式中，矩阵Y为雅克比矩阵J的逆矩阵。因此，

其中，

根据麦克斯韦方程，电场可以由式（11）给出：

电场强度被视为独立变量。因此，

其中：(x) 为配点x上i方向的电场强度；{P(ξ)}T=(1ξ1ξ2ξ1ξ2)，为位移模式向量；为广义坐标。

由于电势和电场强度的电学约束通过在高斯点处配点得到满足，故由使在局部坐标系(，)上单元V中选高斯点的配点xc处的两个近似值相等来确定，即

因此，结合式（11）和式（12），推导出：

为位移模式矩阵。

因此，

式中为有限元节点坐标转换矩阵。

将式（14）代入式（13）推导得

式中，为电场强度转换矩阵，Si(ξ)为电场强度梯度转换矩阵。

电场强度矢量梯度可推导为

其中，

应变张量可以通过类似的推导得到。它的表达式可以从单元V内部的几何关系中获得：

应变张量也设为独立变量，因此，

类似地

应变的近似值可以表示为

其中，{L(ξ)}T={P(ξ)}TA-1，L(ξ)为位移应变转换矩阵。

最后，推导出应变场

应变梯度的近似值可以表示为

其中，{Sk(ξ)}T={P，k(ξ)}TA-1。

因为

式中，(ξ)、(ξ)为位移应变梯度转换矩阵Ψa的子矩阵。

应变梯度场可以表示为

结合式（15）、（16）、（23）、（28），变分公式式（5）可以简化为

UEL 子程序中，以上方程的代码编译流程如图1所示。在开始高斯循环后，根据形函数和在高斯点上的配点循环推导雅可比矩阵。接下来，重新定义本构方程，并根据生成的应力和应变矩阵更新应力和应变值。最后，利用计算过程中的状态变量导出刚度矩阵，结束高斯循环。

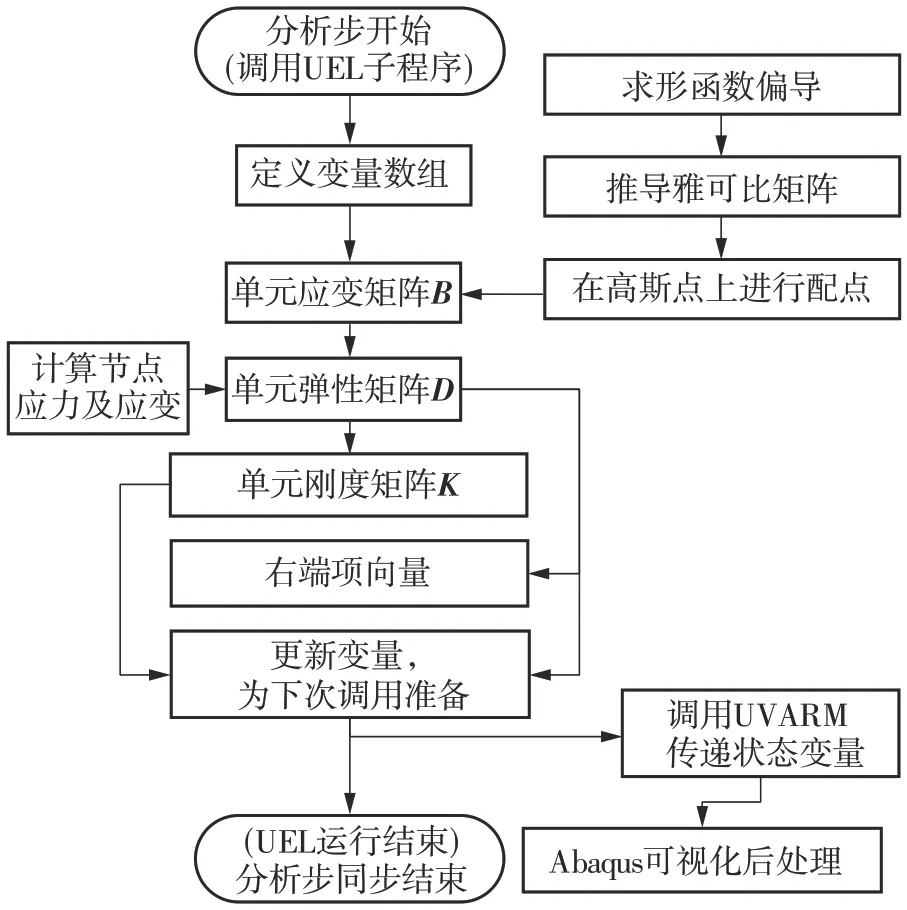
图1 UEL子程序编译流程图Fig.1 Compilation flow chart of UEL

2 验证及网格收敛性分析

本研究选用挠曲电梁验证UEL子程序。计算模型如图2所示，梁的左端边界固支，右端受一竖向集中力Q作用，且右侧边缘的电学边界条件为接地。通过在Abaqus 中进行几何建模、材料定义和网格划分并编写好INP文件完成前期工作，随后调用UEL子程序完成数值仿真。值得注意的是，使用UEL子程序计算后，Abaqus可视化模块中只显示积分点的相关信息。另编写UVARM 子程序，将积分点的结果映射到几何节点以便分析和获得结果。因此，本研究得到的结果是后处理的结果。

图2 纳米悬臂梁Fig.2 Nano cantilever beam

悬臂梁的几何尺寸为长度D=500 nm，厚度W=20 nm，宽度b=10 nm，集中力Q=1 nN。材料选取PZT-5H，其材料参数为E=126 GPa，ν=0.2，l=2 nm，f1=f2=1.0×10-7C/m，a=13×10-9C2/（N·m-2）。图3为悬臂梁在集中荷载下的机电耦合响应。

图3 悬臂梁的力电耦合响应Fig.3 Electromechanical coupling response of cantilever beams

观察图3（a）中的挠度分布，悬臂梁在端部荷载作用下，挠度沿着长度方向逐渐增加，并呈现立方变化，且梁在自由端取得最大挠度40 nm。将仿真结果与Zhang 等［24］计算所得解析解进行对比，结果如图4（a）所示，挠曲电悬臂梁的挠度结果高度一致。

图4 本研究有限元法与解析解［24］、Tian等［17］的有限元解对比Fig.4 Comparison of the FEM in this research with the analytical solution［24］ and the Tian’s results［17］

图3（b）所示悬臂梁的电势沿纵向对称分布，最大电势为38 mV。此外，在靠近固定端的横截面上，电位分布沿厚度方向呈线性变化。悬臂梁模型在固定端的弯矩最大，而在自由端的弯矩为零。根据截面弯矩与应变的计算关系ε=My/EIz（y为距离横截面中心轴的距离，Iz为横截面的惯性矩），弯矩在固定边缘处达到最大，应变梯度达到最大，导致极化最强。图3（c）显示，固定边缘处的电场强度最大，达到3.8 MV/m，这与电势分布结果一致。将电场强度仿真结果与Zhang 等［24］计算所得解析解进行对比，如图4（b）所示。可见，结果的一致性略微差于挠度。由图4可知，本研究采用的基于Abaqus平台开发的有限元法，与其他有限元法的挠度与电场强度指标相比，比其他方法都更接近解析解。这验证了本研究采用的数值方法的有效性。

在Abaqus的有限元模拟中，需要足够精细的网格以确保计算结果的精度，网格过粗会导致结果不准确。涉及高阶弹性和高阶电场的计算需要更密集的网格。然而，随着单元数ρ的增加，用于求解的计算机资源也将增加。因此，在收敛的前提下，控制单元数量来控制计算成本和结果精度之间的平衡非常重要。lnρ可用于表征网格密度，中央处理器（CPU）计算总时间可用于表征计算资源消耗。从图5可以看出，当单元数为3 000时，计算结果趋于收敛，计算资源消耗适中。可以说，此时计算结果的有效性和计算速度之间达到了平衡。因此以下计算均选择这个网格密度进行模拟分析。

图5 不同网格密度下的电场E3和CPU总时间Fig.5 Electric field E3 and total CPU times under different mesh density

3 数值案例

3.1 边界条件对挠曲电矩形梁力电耦合响应的影响

本节对不同约束条件下的矩形梁和弧形梁进行模拟，以研究不同约束条件下不同梁的机电耦合响应特性和能量采集效率。所有模型均在梁的上表面施加1 nN的均布载荷。首先研究支承方式对开路电压的影响，在左侧边缘为铰链支座的情况下，将活动铰链支架从X=0.05D移动到X=D，如图6 所示。当活动铰链支座非常靠近左侧边缘时，结构逐渐转变为几何可变系统，当X/D接近0时，存在结构失效的风险，故研究从X=0.05D开始。

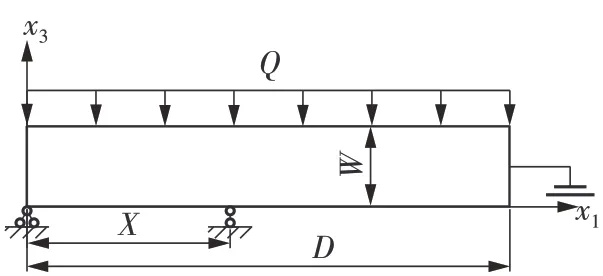
图6 均布荷载下的简支梁Fig.6 Simply supported beam under uniformly distributed loads

图7示出了支座移动时梁的开路电压、最大挠度以及x方向应变在y上的梯度绝对值|η113|的关系。在矩形梁中应变梯度|η113|对挠曲电效应起控制作用，故本研究取应变梯度|η113|进行量化分析。当X/D接近0时，梁的挠度迅速增加。此时简支梁逐渐转变为几何可变系统，梁的开路电压迅速增加。这是由于此时支座附近的应变场急剧变化，导致应变梯度增大，最后提高挠曲电梁的开路电压。当X/D=0.690时，梁的挠度达到最小，为0.19 nm。当X/D=0.750时，梁取得最小开路电压4.25 mV，此时梁的应变梯度|η113|也取得最小值26.9 mm-1。此时，梁的弯矩与应变梯度均为一个较小值。可移动铰链支座向右移动，梁的开路电压、挠度以及应变梯度|η113|增加。当X/D=1.000时，纳米梁为典型简支梁。此时，纳米梁的开路电压、挠度和应变梯度|η113|分别为9.63 mV、1.58 nm 和642.9 mm-1。

图7 铰链支座移动时的开路电压、挠度以及应变梯度|η113|Fig.7 Open-circuit voltage，deflection，and strain gradient|η113| when the hinge support is moving

一般情况下，简支梁的弯矩及应变梯度比起悬臂梁都更小。类似于压电悬臂梁，挠曲电悬臂梁的力电耦合效应也更显著。如图8所示的悬臂梁的左边缘是滑动支撑的，而活动铰链支架的位置从X=0变为X=D。

图8 均布荷载下的悬臂梁Fig.8 Cantilever beam under uniform load

图9 示出了铰链支座从0 移动到D时，梁的开路电压、最大挠度和x方向应变在y上的梯度的绝对值|η113|。当活动铰链支座设置在X/D=0.550时，梁挠度最小，为0.66 nm。当活动铰链支座设置在X/D=0.575时，梁的开路电压最小，为7.86 mV，此时梁的应变梯度|η113|为60.5 mm-1。当活动铰链支座设置在X/D=0 和X/D=1.000时，整个梁的最大挠度分别为15.23 nm和25.30 nm，开路电压分别为40.37 mV和38.72 mV，应变梯度|η113|为272.2 mm-1和243.1 mm-1。X/D=0.100 以左和X/D=0.900 以右的曲线趋势不同。这是因为，纳米梁即将完全转变为悬臂状态。纳米梁的弯曲状态转变为一侧完全受拉，另一侧受压，此时竖向的应变的梯度最大。虽然当X/D=0 和X/D=1.000时，梁的最大弯矩相同，但梁的弯矩图与梁形成的图形中，X/D=1.000 时有较大的面积。根据结构力学知识可知，此时梁的挠度更大。因此，当X/D超过0.900时，挠度增加得更快。当X/D小于0.100时，梁的挠度增加较慢。当X/D=0和X/D=1.000时，纳米梁的电势云图分布相似。X/D=0和X/D=1.000时，梁的最大弯矩相同，但梁的受弯状态并不完全相同，故应变梯度不同，这导致了最后开路的不同。与图7的简支梁情况一样，此时在应变梯度稍大的X/D=0 一侧开路电压更大。

图9 铰链支座从X=0 移动到X=D 时的开路电压、挠度和应变梯度|η113|Fig.9 Open-circuit voltage，deflection，and strain gradient|η113| when the hinge support moves from X=0 to X=D

由此可知，矩形梁如果需要俘获较大的开路电压，边界条件可以是悬臂，也可以是一端滑动另一端简支。然而一端滑动另一条端简支条件下支座边缘最大位移比普通悬臂梁最大位移大66%。这是由于挠曲电效应的本质是应变梯度诱导的极化效应。当弯矩较大，沿垂直方向的应变具有较大的梯度，因此可以获得更强的极化。悬臂边界条件与图6中左侧边缘简支的边界相比，在确保结构正常工作的前提下，可以获得更强的力电耦合响应。图7 和图9 的结果与挠曲电效应本构方程式（2）相符，即极化由挠曲电系数和应变梯度大小决定。由此，在使用同一材料设计挠曲电梁时，可通过控制变形梯度来控制输出电压的大小。

3.2 圆心角对挠曲电弧形梁力电耦合响应的影响

异形梁如弧形梁因其结构不规则，应变分布不规则，应变梯度更大，挠曲电效应更为显著。，对矩形梁进行弯曲，可以有效增大开路电压。Sladek等［21］对小曲率弧形梁的挠曲电响应进行了理论分析，其推导结果表明，改变梁的曲率可有效地增大挠曲电悬臂梁的开路电压。根据Sladek等［21］的计算，梁的E3从矩形梁到圆形角为0.95°的弧形梁，增加了四分之一。对悬臂梁和一端滑动、另一端简支的矩形梁进行类似弯曲，并研究大曲率的挠曲电弧形梁的力电耦合响应，结构示意图如图10所示。

图10 竖向均布荷载下的弧形梁Fig.10 Curved beam under vertical uniformly distributed load

当弧形梁的边界条件为左端固定，研究弧形梁在1 nN 竖向均布荷载作用下，圆心角取值-90°至90°的挠曲电响应。模拟不同圆心角悬臂梁的挠曲电响应，汇总得到图11（a）。其中0°到90°表示梁向下弯曲，-90°到0°表示梁向上弯曲。当圆形角为0°时，梁处于直梁状态，梁的挠度最大，但与弯曲情况相比，开路电压较小。这表明改变梁的弯曲程度，可有效提高梁输出的开路电压，减小梁的挠度。相同弯曲程度下，弧形悬臂梁向下弯曲的开路电压大于弧形悬臂梁向上弯曲的开路电压。当弧形悬臂向下弯曲且圆心角为52°时，获得的开路电压最大，其值为102.47 mV，比相同条件下矩形梁的40.37 mV大153.8%。

图11（b）示出了弧形梁在左端滑动约束和右端铰接的边界条件下，向上和向下弯曲的挠曲电响应。与弧形悬臂梁一样，圆心角的正负也代表弧形梁的弯曲方向。同样，当梁为直梁时，梁的挠度最大，但开路电压远小于弧形梁。在一定范围内增加弧形梁的弯曲程度也可以增加开路电压，减小挠度。然而，与悬臂梁不同的是，无论是向上弯曲还是向下弯曲，弧形梁在左端滑动约束和右端铰接的边界条件下产生的最大开路电压都更大。如图11（b）所示，当弧形梁向上弯曲且圆心角为38°时，取得最大开路电压214.07 mV。这是弧形悬臂梁边界条件下最大开路电压102.47 mV 的两倍多，是矩形悬臂梁的5倍以上。此外，若将挠曲电系数设置为0 C/m，材料PZT-5H 仅考虑其压电效应，在该模型中，没有挠曲电效应的情况下，开路电压将降低89.3%。

4 结语

基于UEL子程序二次开发将挠曲电本构模型内化到有限元软件Abaqus中，实现了对挠曲电效应的数值模拟，并将单元的DOFs 减少至12。计算出保证网格收敛和计算效率的最优网格密度。数值模拟了纳米矩形梁和纳米弧形梁在不同边界条件下的挠曲电响应。结果表明，在均布荷载作用下，以中心角38°向上弯曲的受一边滑动和一边铰接约束的弧形梁，取得弧形梁的开路电压最大值。本研究通过数值模拟，直观地展现了挠曲电梁中应变梯度对梁力电耦合响应的影响。在设计挠曲电结构时，为获取更大的输出电压，应从增大变形梯度的角度入手。本研究提供了一种在通用有限元软件中分析挠曲电微纳结构的有效方法，可用于Abaqus 中大型挠曲电结构建模和计算。在大变形的情况下，上述数值方法也适用，例如挠曲电蜂窝结构的模拟。通过处理状态变量并通过UVARM 子程序输出，还可以自由输出其他挠曲电结构的场量，例如强度因子和J积分等参数，这些参数是材料断裂计算中的重要参数。通过显式动力分析用户自定义单元子程序（VUEL）进一步开发，还可以在Abaqus 中实现挠曲电结构的动力响应分析。